Презентация на тему Механические волны

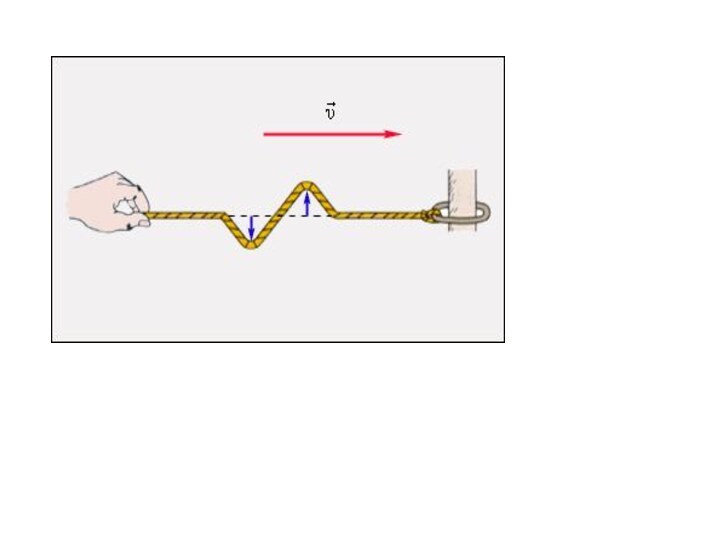
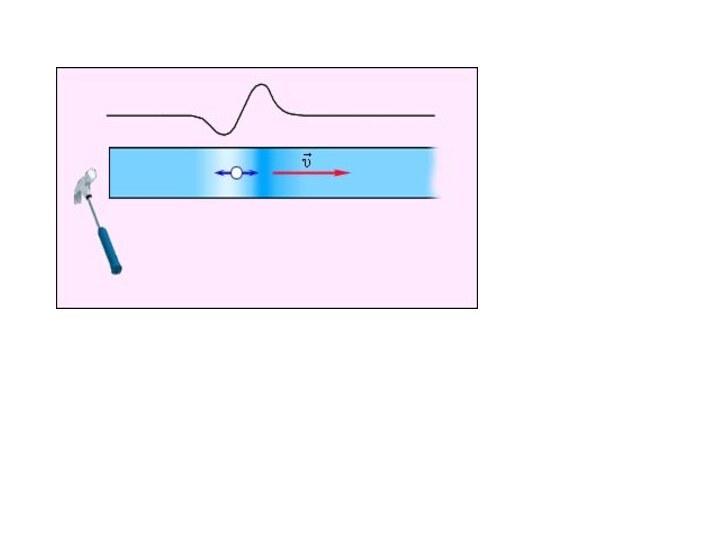
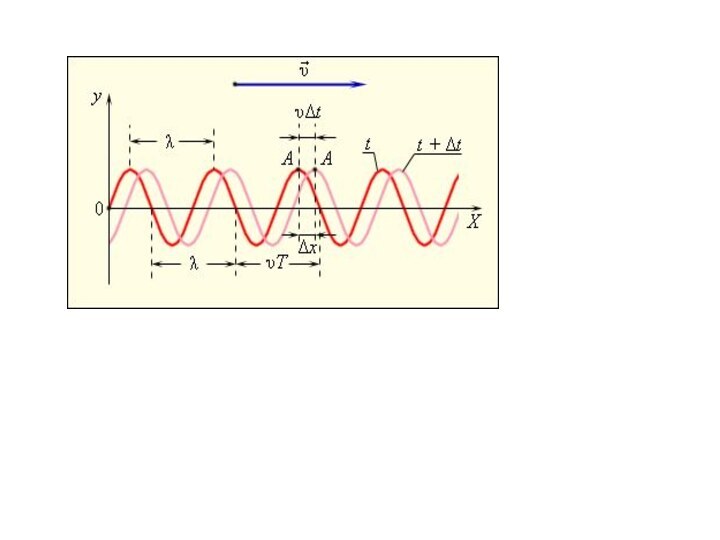
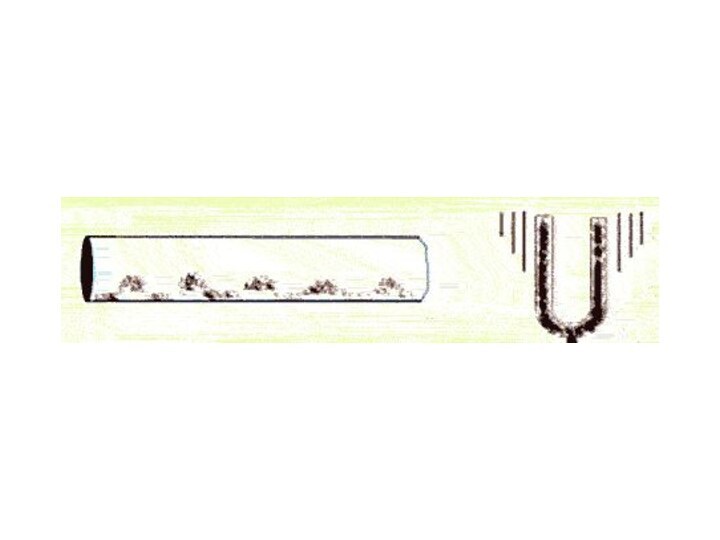
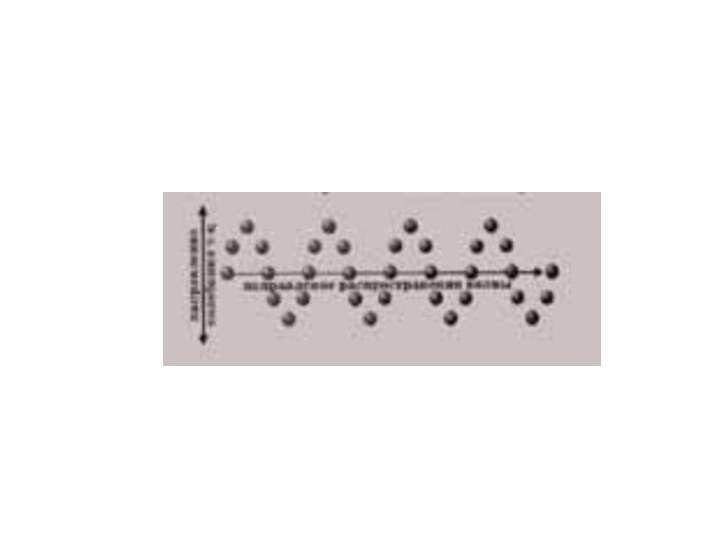
синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой

ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Смещение y(x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:

волновое число, ω = 2πν – круговая частота

точками на оси OX, колеблющимися в одинаковых фазах. Расстояние,

равное длине волны λ, волна пробегает за период T, следовательно, λ = υT, где υ – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки A на рис. 2.6.4) выражение ωt – kx не изменяется по величине. С течением времени t изменяется и координата x этой точки. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:

– во времени и пространстве. Временной период равен периоду

колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число

является пространственным аналогом круговой частоты

гармонические колебания с некоторой частотой ω. Поэтому, как и

в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме.
При распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.