Слайд 5
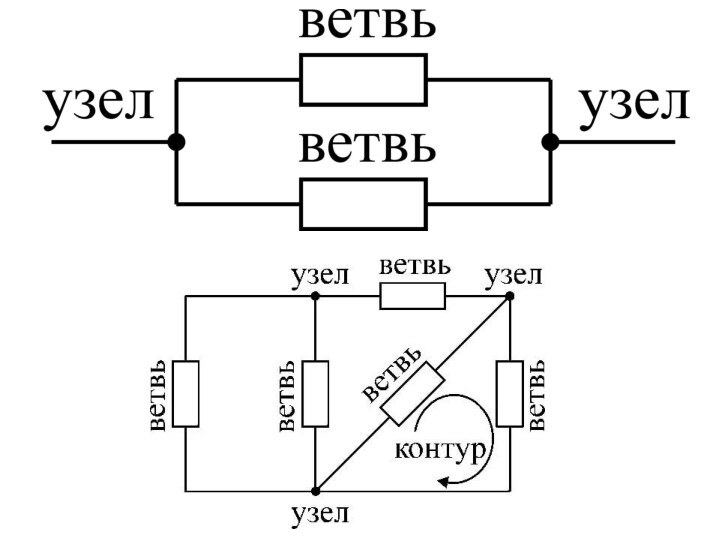
Если в контуре не окажется ни последовательно, ни
параллельно соединённых проводников, для вычисления общего сопротивления следует использовать
следующие свойства электрической цепи:
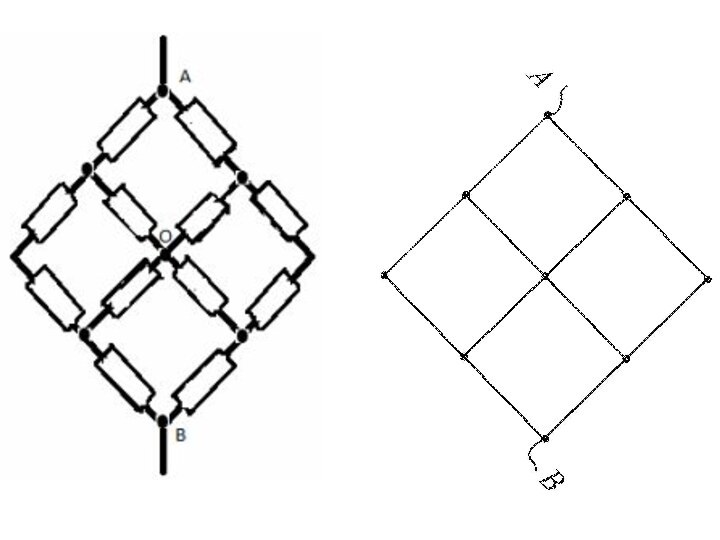
В электрической цепи точки с одинаковыми потенциалами можно соединять или разъединять. Поскольку ток между такими точками не идёт, то общий режим тока в цепи при этом не меняется.
Слайд 7
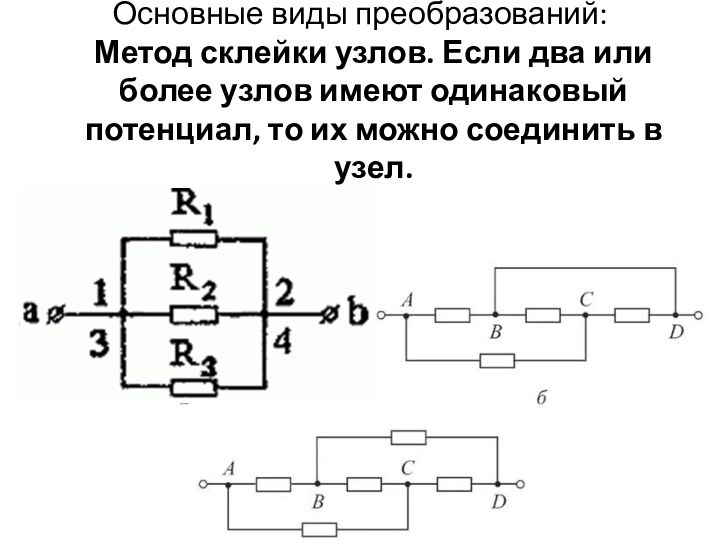
Основные виды преобразований:
Метод склейки узлов. Если два или
более узлов имеют одинаковый потенциал, то их можно соединить
в узел.
Слайд 8
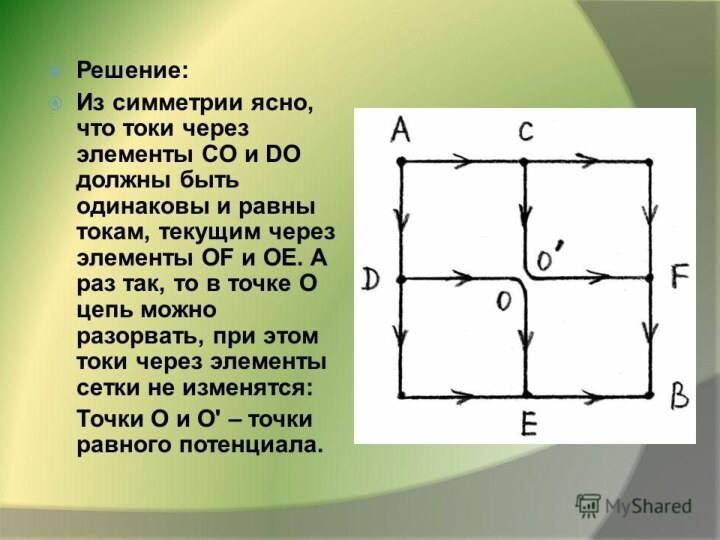
Метод равных потенциалов.
Точки с одинаковыми потенциалами всегда есть
в схемах, обладающих осью или плоскостью симметрии относительно точек
подключения. Возможны два случая.
Если схема симметрична относительно оси (плоскости), проходящей через точки входа и выхода тока (имеется продольная ось симметрии), то точки одного потенциала находятся на концах симметричных резисторов, поскольку по ним идут одинаковые токи.
Слайд 9
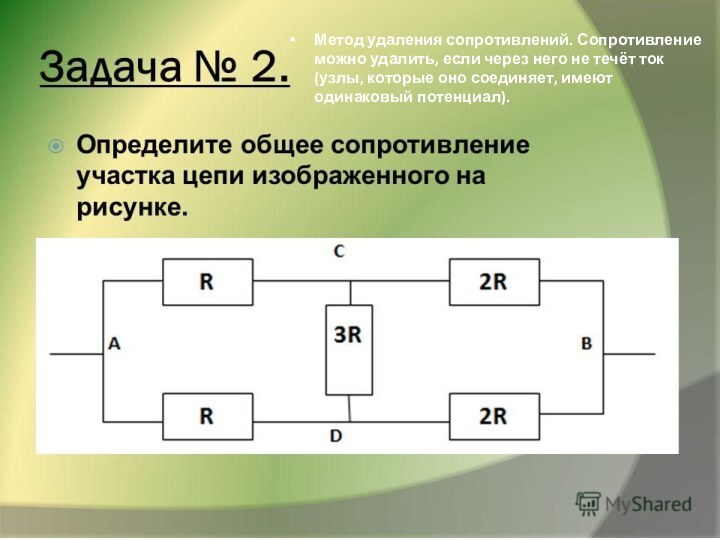
Метод удаления сопротивлений. Сопротивление можно удалить, если через
него не течёт ток (узлы, которые оно соединяет, имеют
одинаковый потенциал).
Слайд 11
Если схема симметрична относительно оси (плоскости), перпендикулярной линии,
на которой лежат точки входа и выхода тока -
в схеме имеется поперечная ось (плоскость) симметрии, то одинаковым потенциалом обладают все точки, лежащие на пересечении этой оси (плоскости) с проводниками. Это утверждение вытекает из того, что работа электрических сил не зависит от формы пути.
Слайд 12
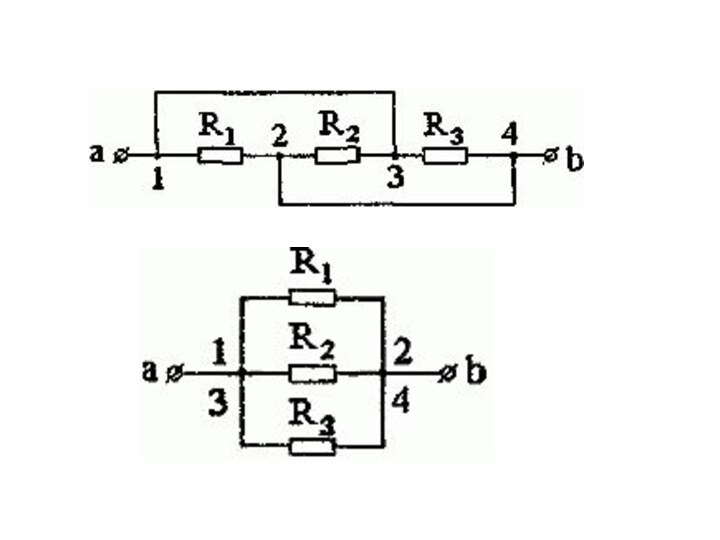
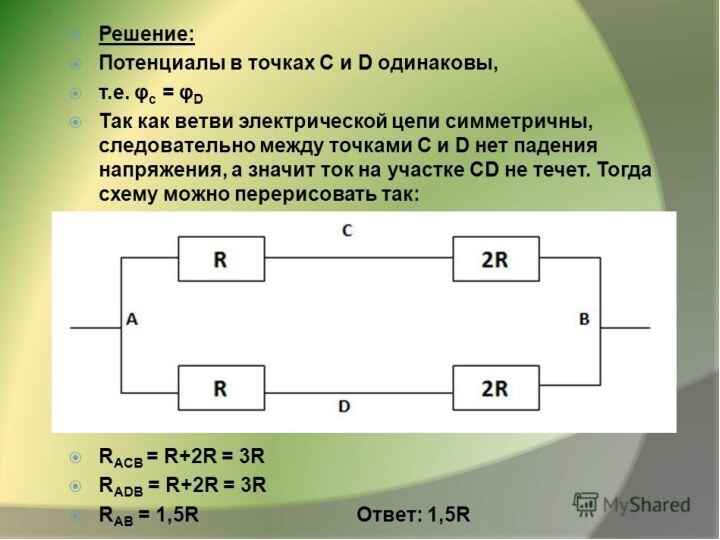
Найдя в схеме точки с одинаковыми потенциалами, можно
произвести такие её преобразования, что останутся только параллельные и
последовательные соединения. Основные виды преобразований:
Метод склейки узлов. Если два или более узлов имеют одинаковый потенциал, то их можно соединить в узел.
Метод удаления сопротивлений. Сопротивление можно удалить, если через него не течёт ток (узлы, которые оно соединяет, имеют одинаковый потенциал).
Метод разрезания узлов. Действие, противоположное склейке: разъединив центральный узел на несколько, можно получить несколько узлов с равными потенциалами.
Слайд 13
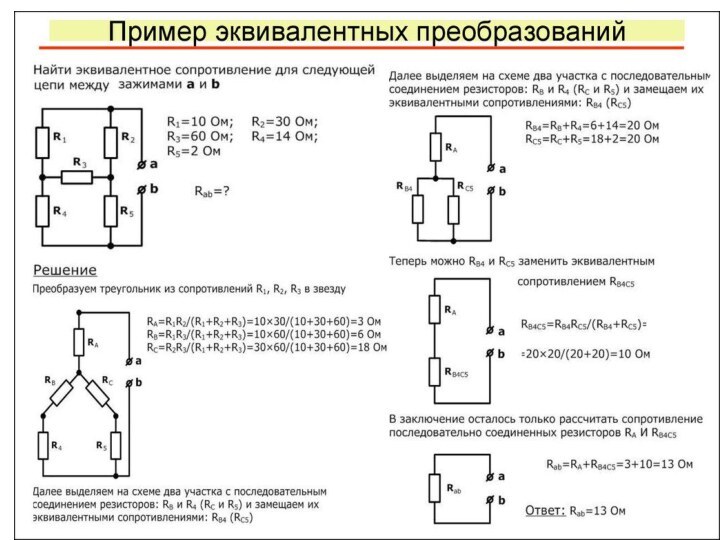
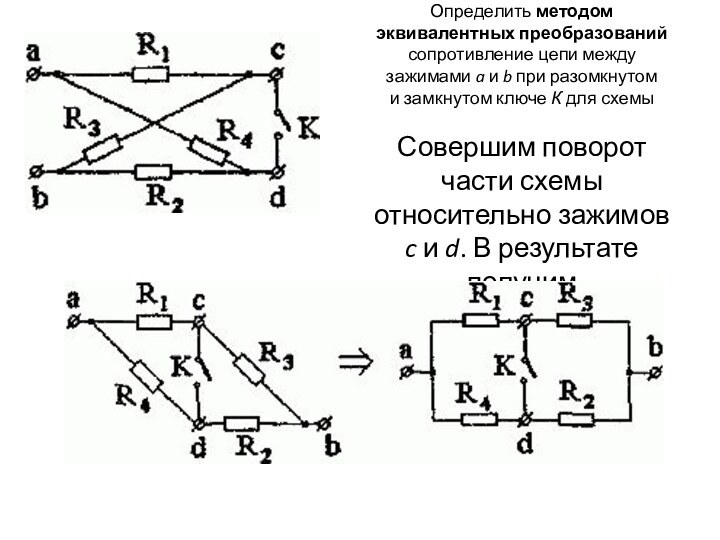
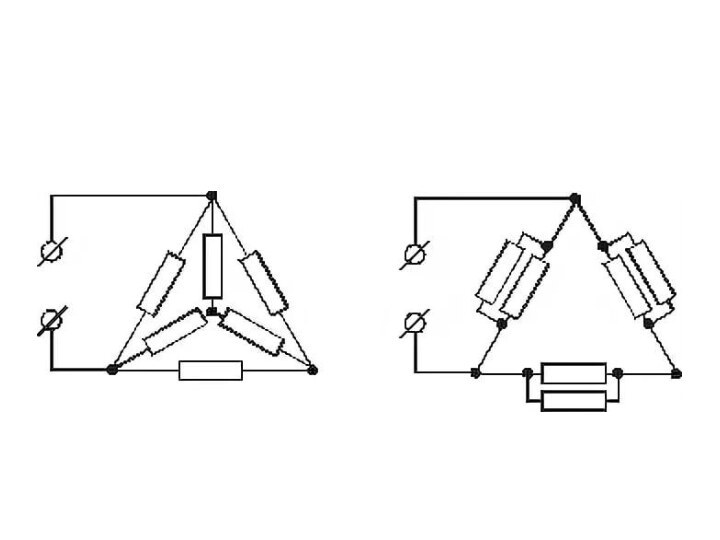
Определить методом эквивалентных преобразований сопротивление цепи между зажимами
a и b при разомкнутом и замкнутом ключе К для схемы
Совершим поворот части
схемы относительно зажимов c и d. В результате получим
Слайд 15
Метод разрезания узлов. Действие, противоположное склейке: разъединив центральный
узел на несколько, можно получить несколько узлов с равными
потенциалами.
Слайд 24
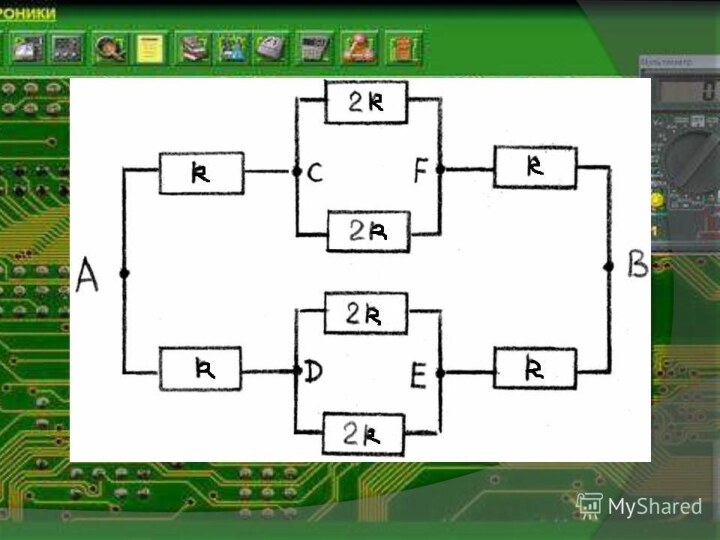
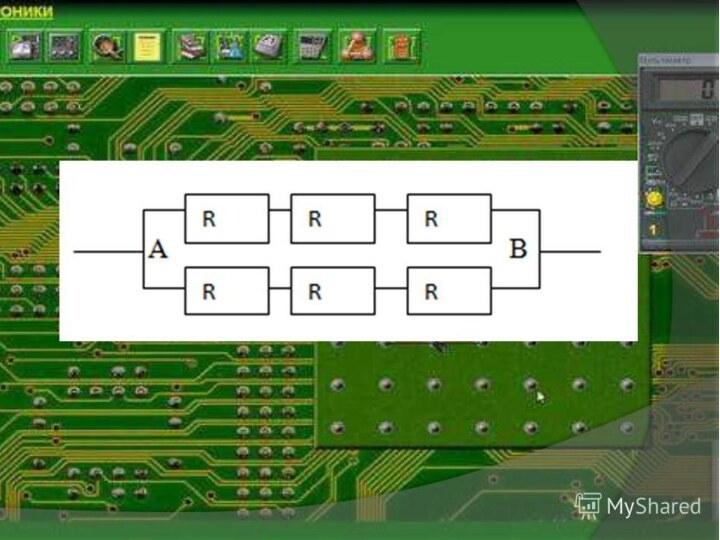
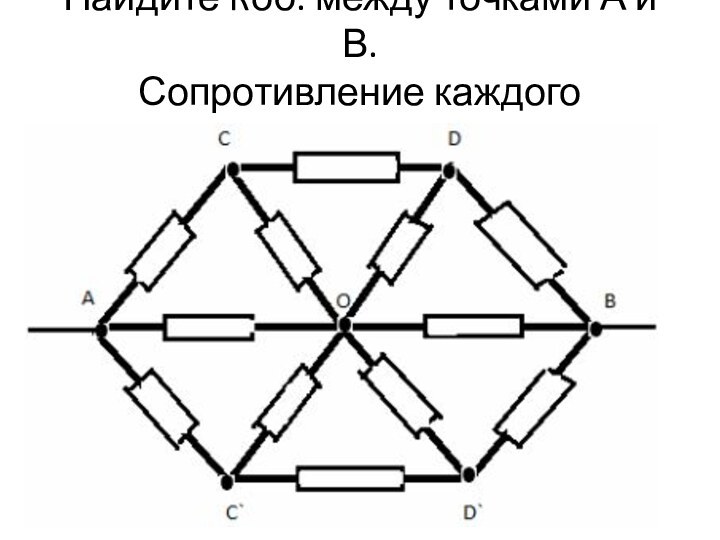
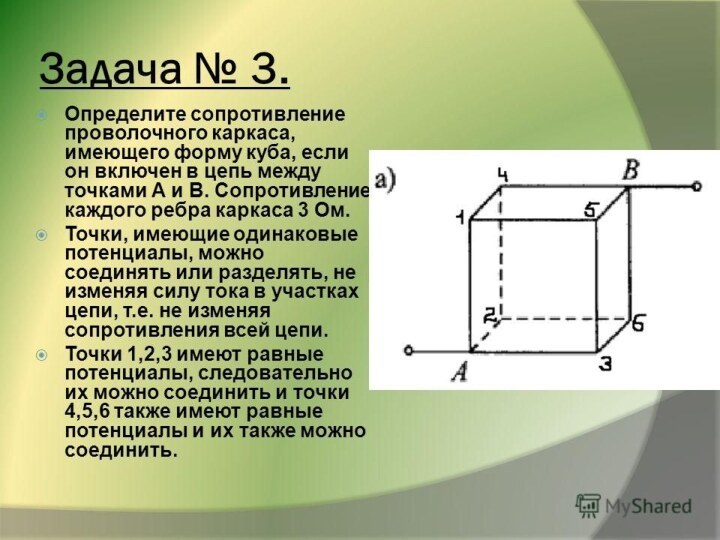
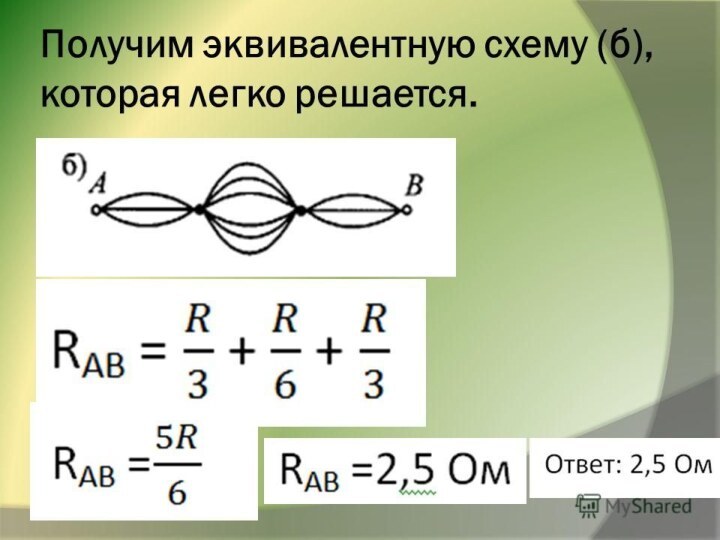
Найдите Rоб. между точками А и В.
Сопротивление каждого
резистора R
Слайд 32
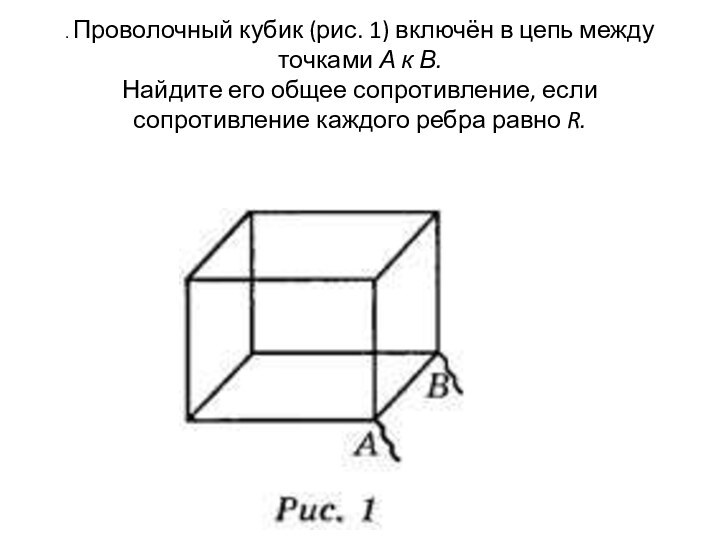
. Проволочный кубик (рис. 1) включён в цепь
между точками А к В.
Найдите его общее сопротивление, если
сопротивление каждого ребра равно R.
Слайд 33
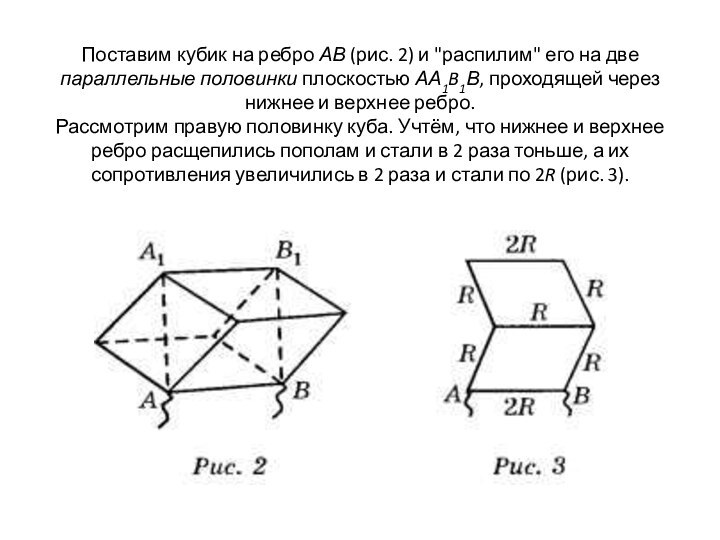
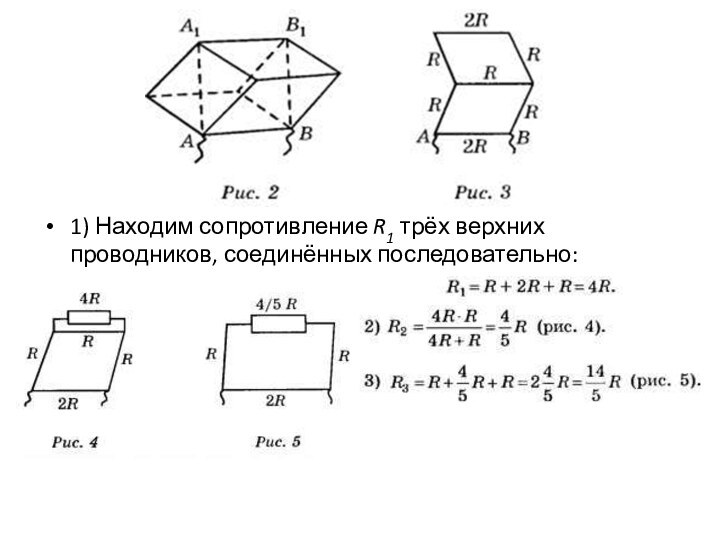
Поставим кубик на ребро АВ (рис. 2) и
"распилим" его на две параллельные половинки плоскостью АА1B1В, проходящей
через нижнее и верхнее ребро.
Рассмотрим правую половинку куба. Учтём, что нижнее и верхнее ребро расщепились пополам и стали в 2 раза тоньше, а их сопротивления увеличились в 2 раза и стали по 2R (рис. 3).
Слайд 34
1) Находим сопротивление R1 трёх верхних проводников, соединённых
последовательно:
Слайд 35
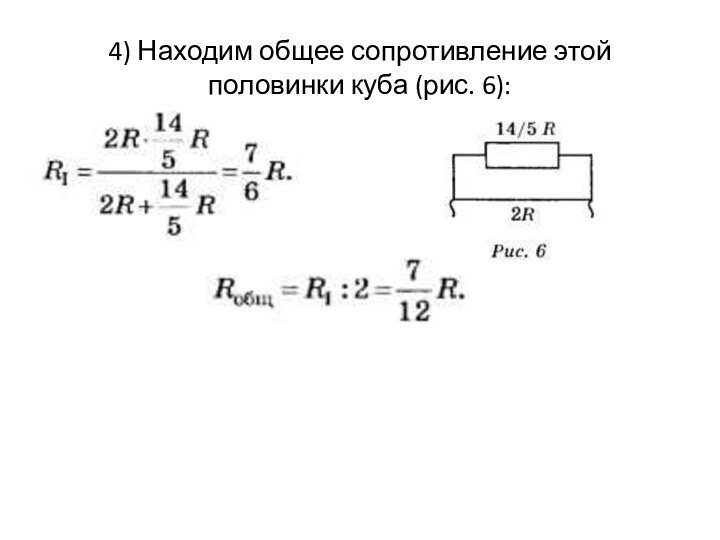
4) Находим общее сопротивление этой половинки куба (рис.
6):
Находим общее сопротивление куба:
Слайд 36
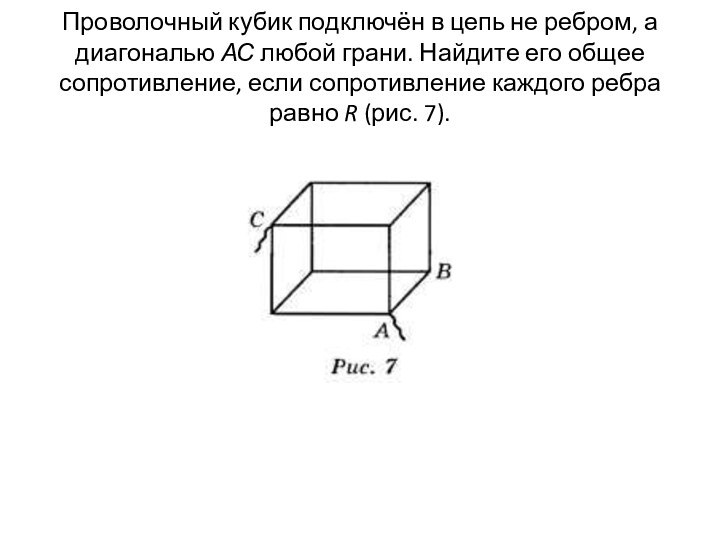
Проволочный кубик подключён в цепь не ребром, а
диагональю АС любой грани. Найдите его общее сопротивление, если
сопротивление каждого ребра равно R (рис. 7).
Слайд 37
Снова ставим кубик на ребро АВ. "Распиливаем" кубик
на две параллельные половинки той же вертикальной плоскостью (см.
рис. 2).
Опять рассматриваем правую половинку проволочного куба. Учитываем, что верхнее и нижнее ребро расщепились пополам и их сопротивления стали по 2R.
С учётом условия задачи имеем следующее соединение (рис. 8).
Дальше ещё проще. Так как ток по ребру а—b не идёт, то это ребро из цепи можно удалить (рис. 9).
Слайд 38
1) Находим R1= 2R + R + R +
2R = 6R.
2) R2= R + R = 2R.
3) Общее сопротивление
половинки куба
Общее сопротивление обеих параллельно соединённых половинок