Слайд 2
Пи-Теория фундаментальных физических констант исходит из следующих предположений:
1. Физическая реальность существует как компромисс между полным наличием
и полным отсутствием самой себя.
2. Для определения пространственно - временных параметров физической реальности достаточно системы единиц LT и числа пи.
3. Физическая масса M есть площадь эквивалентная данной физической массе.
4. Физическая реальность, формируя метрический интервал должна полностью скомпенсировать эквивалентным ему псевдометрическим интервалом .
С и Т - скорость и время компенсации.
5. Скорость распространения взаимодействий конечна.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 3
Компенсационный принцип (далее К-принцип), запишем как:
где n –
размерность пространства.
К-принцип, в общем случае, можно записать как:
или:
и - значения размерного или безразмерного параметра физической реальности, находящиеся в пределах:
N - целое число, находящееся в пределах
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 4
6.Физическая реальность существует только в границах своих параметров
L и T:
- предельные значения параметров L и T физической реальности.
7. Безразмерные фундаментальные физические постоянные не изменяются со временем.
8. Справедлив принцип причинности.
9. Выполняется принцип эквивалентности.
Запишем в системе единиц LT широко известные планковские параметры физической реальности:
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
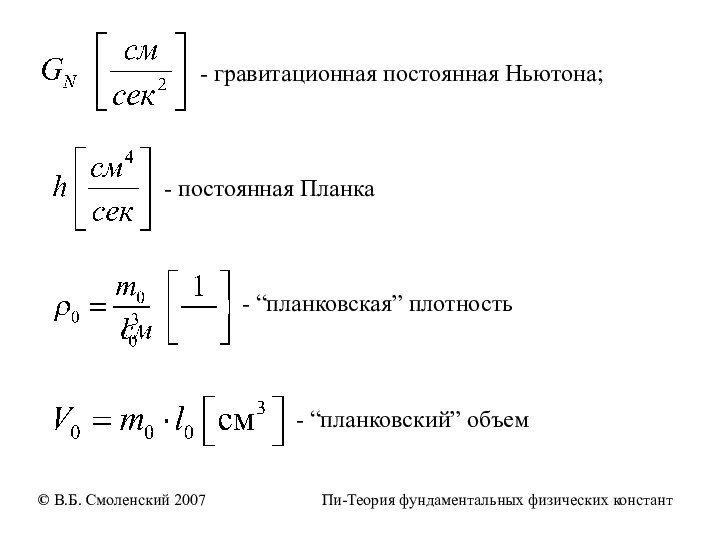
- гравитационная постоянная
Ньютона;
- постоянная Планка
- “планковская” плотность
- “планковский” объем
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 6
Определим постоянную
Представим
в виде:
где - некоторая безразмерная постоянная, тогда:
где и – соответственно масса и комптоновская длина волны электрона.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 7
В виду того, что:
Уравнение взаимосвязи фундаментальных физических
констант запишется как:
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 8
Уравнение взаимосвязи фундаментальных физических констант
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 9
Уравнение для расчета элементарного объема
Из последнего уравнения следует,
что электрон должен иметь массу покоя, т.к. при любом
изменении элементарный объем не будет постоянным.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 10
Уравнение для
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 11
Уравнение для расчета гравитационной постоянной
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 12
Фазовый радиус вселенной
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 13
Фазовый и метрический объемы тела
NT – число частиц составляющих тело.
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 14
Всегда должны выполняться соотношения:
- ускорение тела
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 15
уравнение взаимосвязи фундаментальных физических констант
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 16
применение К-принципа (частный случай)
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 17
Земля
© В.Б. Смоленский
2007
Пи-Теория фундаментальных физических констант
Слайд 18
Определим абсолютную пустоту как некую параметрическую абстракцию -

среду, которой нет и в которой ничего нет. Тогда,
условно говоря, в такой среде нельзя создать или определить даже одну точку, ведь среды нет. Определим абсолютную полноту как сплошную среду, которая есть и в которой все есть. Тогда мы не сможем уничтожить или определить точку в этой сплошной среде, потому что точки среды должны отличаться друг от друга, а отличий нет. Даже нет понятия точки, потому что среда сплошная. Если мы не можем определить точку в среде, то значит, мы не можем судить о среде, т.е. чем является среда: абсолютной пустотой или абсолютной полнотой. Каким образом такие сущности как абсолютные пустота и полнота могут проявить себя? Предположим, что Природа не может реализовываться или существовать в виде только абсолютной пустоты или только абсолютной полноты. Тогда, если это так, Природа делает выбор, если реализует только один из вариантов: или абсолютная пустота или абсолютная полнота. Представляется верным предположить, что должен быть компромисс в виде реализации компенсационного принципа, т.е. Природа существует одновременно как абсолютная пустота и как абсолютная полнота, которые каким-то образом скомпенсированы.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 19
Добавление хотя бы одного элемента к абсолютной пустоте
делает ее не абсолютной пустотой. Уменьшение абсолютной полноты хотя
бы на один элемент делает ее не абсолютной полнотой. Как Природа может изменить (уменьшить) абсолютную полноту и изменить (увеличить) абсолютную пустоту? Природа подчиняется следующему компенсационному уравнению:
тогда:
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 20
Пусть выполняется соотношение:
Пусть появился только один 0-мерный
объем, т.е. выполняется условие:
Тогда:
Причем появился именно 0-мерный объем,
а не его ордината, т.к. в силу соотношения:
ордината объема нулевой размерности не определяется.
вместе с должен появиться 0-мерный объем :
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
или
Получается, что одновременно должны
существовать объемы
и , причем:
Тогда можно записать:
Мы имеем своеобразный принцип неопределенности: неизвестно, содержит ли единичный 0-мерный объем только один 0-мерный объем или содержит 0-мерных объемов.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 22
Тогда можно записать:
Исходя из того, что:
Используя соотношение
для К-принципа:
запишем:
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 23
или:
Тогда можно записать:
в общем случае:
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 24
для объемов с размерностью больше нуля выполняется соотношение:
Последняя система уравнений представляет собой ни что иное как
математическую интерпретацию принципа причинности. Природа не может создать вначале объемы с размерностью больше нуля, т.е. метрические объемы, а потом уже нульмерные объемы. Это логически некорректно. Более того, возникает сразу вопрос, а какое количество минимальных метрических объемов нужно создать. Природа, вообще говоря, должна создать, как минимум, хотя бы один физический объект находящийся в двух разных состояниях, например, объект имеющий одновременно минимальный и максимальный метрический объем. Это невозможно, в виду конечной скорости распространения взаимодействий и, если иметь в виду реальный максимальный метрический объем.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 25
Природа создать эти метрические объемы не может, т.к.,
по условию, физический объект одновременно не может находиться в
двух разных состояниях, т.е., в нашем случае, иметь два разных трехмерных метрических объема. И, тем не менее, Природа находит выход из положения. Природа создает один минимальный метрический объем, равный:
или:
Обозначим:
Тогда:
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 26
Запишем для 4-х мерного случая систему уравнений:
Из
системы уравнений следует, что:
Или, в более общем случае:
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 27
Из последнего уравнения мы получаем ответ на вопрос
почему пространство трехмерно.
Потому что, при
, объем запишется как .
Представляется верным интерпретировать это обстоятельство
как запрет Природы на существование объемов отрицательной размерности и, очевидно, как следствие, запрет на существование отрицательных объемов.
Запишем следующие выражения, проясняющие сложившуюся ситуацию.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 28
Выражение:
можно записать в виде:
и в виде:
Записанные уравнения тождественны абсолютно, поэтому Природа должна реализовать оба
варианта. Но мы до этого выяснили, что невозможно одному физическому объекту одновременно находиться в двух различных состояниях, поэтому Природа одномоментно создает:
1.Метрические объемы:
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант
Слайд 29
2. Фазовые объемы:
© В.Б. Смоленский 2007
Пи-Теория фундаментальных физических констант
Слайд 30
Следует иметь в виду, что есть
реальный метрический объем, а - псевдореальный объем,
который равен максимальному значению реального метрического объема
нашей вселенной. Таким образом, вселенная должна расширяться от реального объема до реального объема
равного . Возможен и обратный процесс. В любом случае, на переходный процесс из одного состояния в другое, проходящий с конечной скоростью требуется время. В этом и состоит природа времени. Стрела времени имеет только одно направление.
© В.Б. Смоленский 2007 Пи-Теория фундаментальных физических констант