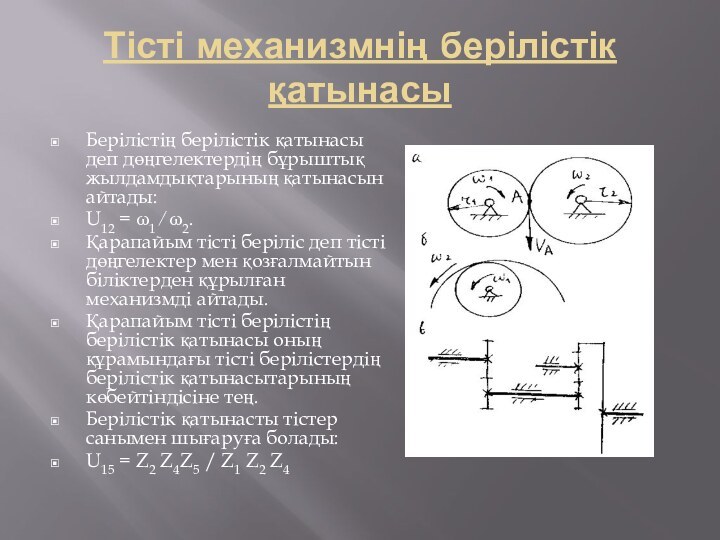
бұрыштық жылдамдықтарының қатынасын айтады:
U12 = ω1 ⁄ ω2.
Қарапайым тісті
беріліс деп тісті дөңгелектер мен қозғалмайтын біліктерден құрылған механизмді айтады. Қарапайым тісті берілістің берілістік қатынасы оның құрамындағы тісті берілістердің берілістік қатынасытарының көбейтіндісіне тең.
Берілістік қатынасты тістер санымен шығаруға болады:
U15 = Z2 Z4Z5 / Z1 Z2 Z4