Презентация на тему Преобразования сигналов и Вейвлет-преобразование

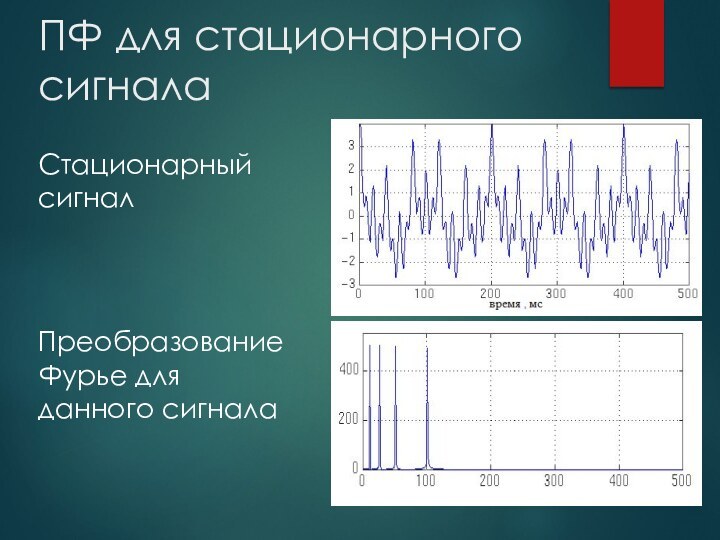
из амплитуды от времени и наоборот.
Проблемы начинаются с появлением

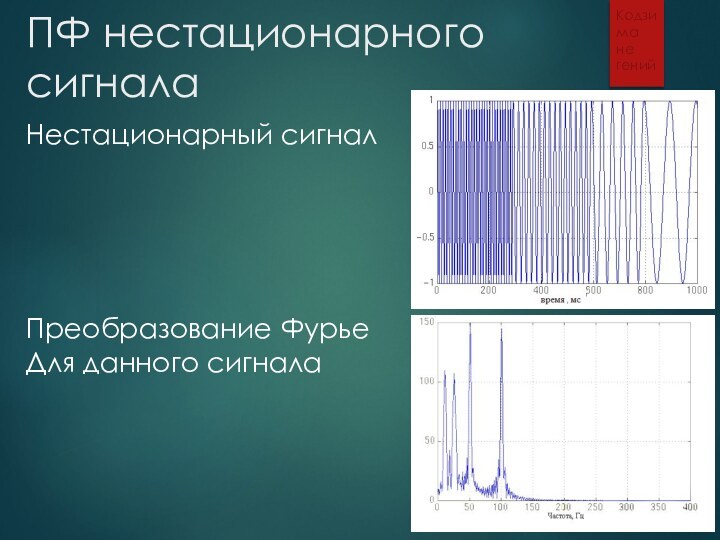
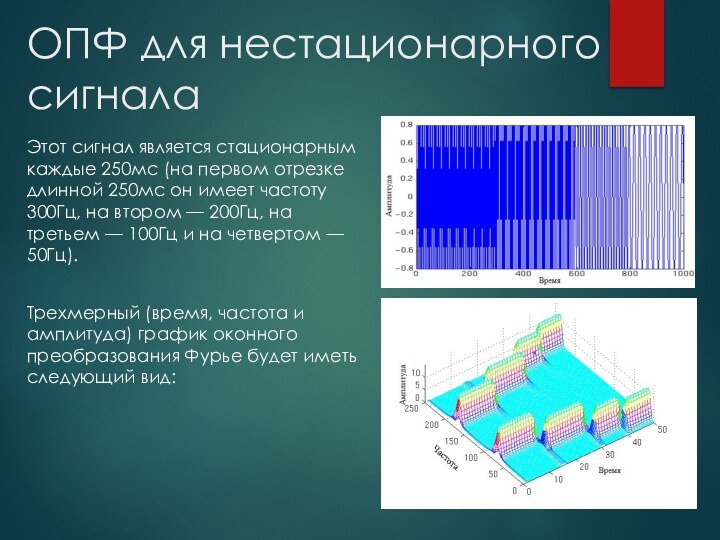
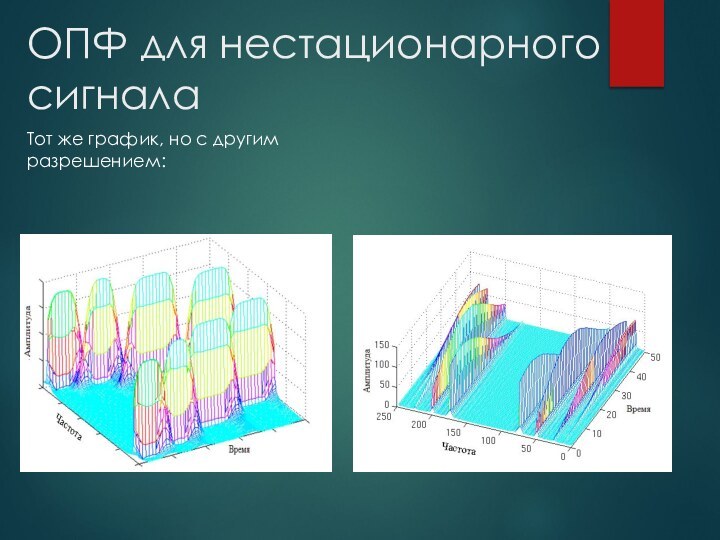
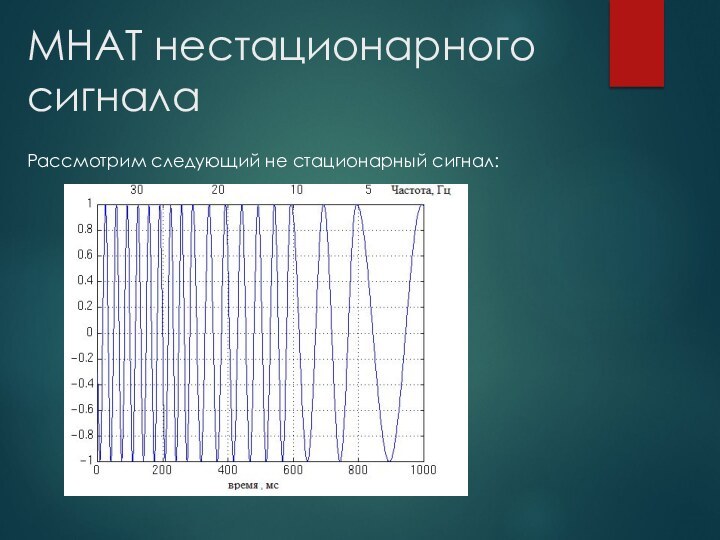
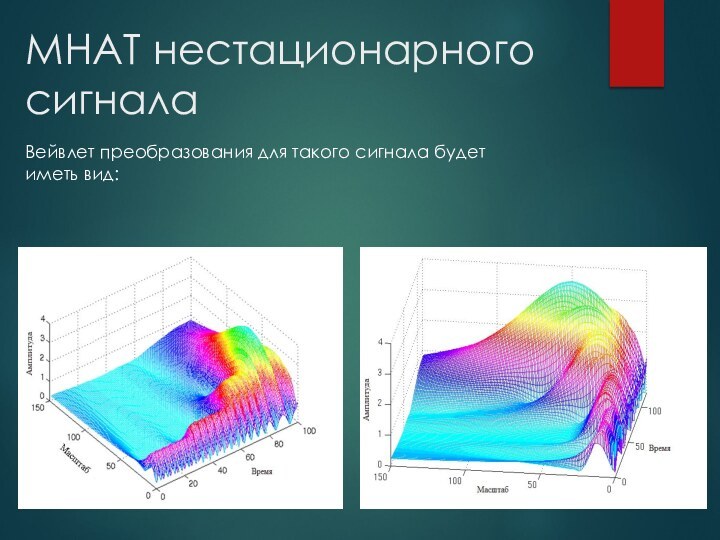
нестационарных сигналов(таких, что их частота не постоянна) потому, что ПФ интегрирует по всему времени, и время существования той или иной частоты неважно: ее вклад останется таким же.
Также ПФ не позволяет получить частотно-временное представление сигнала.

сигнала

данного сигнала

в том, что мы берем промежуток времени достаточно малый

для того, чтобы частота на нем была постоянна.
Здесь можно получить и частотно-временное представление сигнала.
Но и здесь есть проблема: она берет корни в принципе Гейзенберга: невозможно получить точное частотно-временное представление сигнала.
В зависимости от размера окна мы будем получать разные разрешения: узкое обеспечит временное разрешение, широкое — частотное.
При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте!

250мс (на первом отрезке длинной 250мс он имеет частоту

300Гц, на втором — 200Гц, на третьем — 100Гц и на четвертом — 50Гц).

Трехмерный (время, частота и амплитуда) график оконного преобразования Фурье будет иметь следующий вид:

другим разрешением:

формулы)
ψ – материнский вейвлет








Материнских вейвлетов используется немного:
вейвлет Хаара
вейвлет Добеши
вейвлеты Гаусса
вейвлет

Мейера
вейвлет Морле
вейвлет Пауля
вейвлет «Мексиканская шляпа»
вейвлет Койфмана
вейвлет Шеннона

Ага, «немного»