сообщить проводнику , находящемуся вне поля, избыточный заряд, он
распределится только по поверхности проводника так, что напряженность поля в проводнике будет равна нулю. (рис.3.2).рис.3.2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

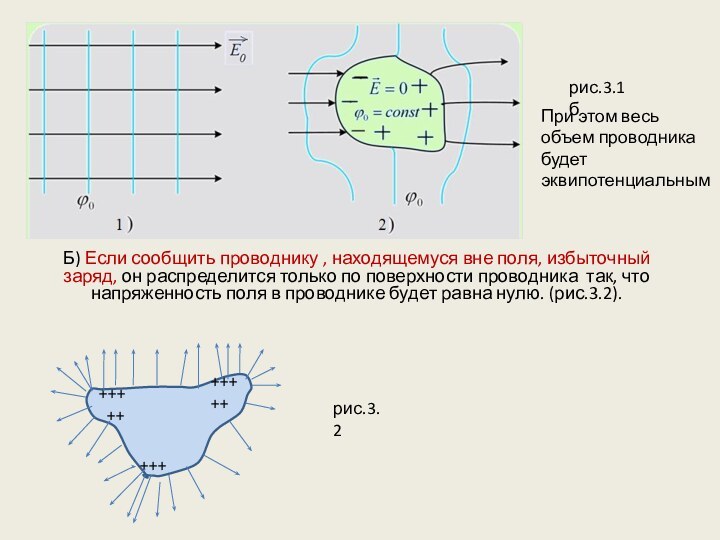


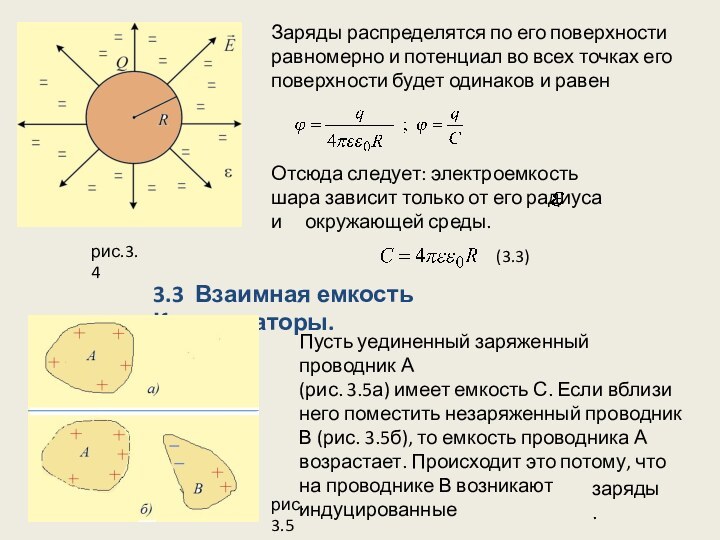






рис.3.2
(3.2)
3.3 Взаимная емкость Конденсаторы.
Пусть уединенный заряженный проводник А
(рис. 3.5а) имеет емкость С. Если вблизи него поместить незаряженный проводник В (рис. 3.5б), то емкость проводника А возрастает. Происходит это потому, что на проводнике В возникают индуцированные
рис. 3.5
заряды.
(3.3)
Емкость уединенного проводника возрастает при приближении к нему другого проводника за счет возникновения взаимной емкости проводников.
В случае двух близко расположенных проводников , несущих заряды + q и –q, разность потенциалов этих проводников
, где -- взаимная емкость двух проводников.
Взаимная емкость двух проводников численно равна заряду, который нужно перенести с одного проводника на другой для изменения их разности потенциалов на 1В.
Практические устройства, позволяющие при малых размерах и небольших накапливать значительный заряд называются конденсаторами.
Чтобы на поле конденсатора не влияли окружающие тела, расстояние между пластинами конденсатора выполняется значительно меньше их размеров
Электроемкость конденсатора – это взаимная емкость его обкладок
.
Конденсаторы бывают плоские, цилиндрические и сферические.
Емкость плоского конденсатора (рис.3.6) :
Все поле сосредоточено между плоскостями, оно является однородным
рис.3.6
Если число зарядов в системе произвольно, энергия i-го заряда
Здесь -потенциал, созданный остальными зарядами в той точке, где находится i-й заряд.
Для всей системы:
(3.5)
Найдем энергию заряженного уединенного проводника, представив его заряд Q как систему точечных зарядов.
Поверхность проводника эквипотенциальна. Поэтому потенциалы точек, в которых находятся точечные заряды , одинаковы (обозначим их ):
3.4 Энергия системы точечных зарядов и заряженного уединенного проводника.
Энергия поля конденсатора:
Выразим энергию поля конденсатора через напряженность поля конденсатора.
- объем пространства между пластинами конденсатора.