Слайд 2
ФИЗИКА – НАУКА О ПРИРОДЕ.
СОВРЕМЕННАЯ ФИЗИКА –
НАУКА, ИЗУЧАЮЩАЯ ОБЩИЕ СВОЙСТВА
МАТЕРИИ – ВЕЩЕСТВА И ПОЛЯ.
Первый шаг при выбранной концепции построения курса физики – Механика рассматривала физические модели: материальная точка и абсолютно твердое тело, не вникая во внутреннюю структуру.
Следующий шаг в познании свойств материи – Статистическая физика устанавливает из каких частей (атомов и молекул) состоит тело, и как эти части взаимодействуют между собой.
Слайд 3
Поскольку атомы построены из электрически заряженных частиц (электронов
и ядер), то следующий шаг в познании строения вещества
– исследование электромагнитных взаимодействий.
Электричество
Электростатика
Постоянный ток
Электромагнетизм
Слайд 4
Исторический очерк. Электрические явления были известны в глубокой
древности.
1) Порядка 500 лет до нашей эры Фалес
Милетский обнаружил, что потертый шерстью янтарь притягивает легкие пушинки. Его дочь пыталась почистить шерстью янтарное веретено и обнаружила этот эффект.
От слова «электрон», означающий по-гречески «янтарь» и произошел термин «электричество». Термин ввел английский врач Гильберт в XVI веке. Он обнаружил, что еще ряд веществ электризуется.
2) При раскопках древнего Вавилона (4000 лет назад) обнаружены сосуды из глины, содержащие железный и медный стержни. На дне битум – изолирующий материал. Стержни разъедены лимонной или уксусной кислотой, то есть находка напоминает гальванический элемент.
3) Золотое покрытие вавилонских украшений можно объяснить только гальваническим способом их нанесения.
Слайд 5
Электростатика – раздел физики, изучающий взаимодействие и свойства
систем электрических зарядов неподвижных относительно выбранной инерциальной системы отсчета.
Электрический
заряд – мера электрических свойств тел или их составных частей.
Термин ввел Б.Франклин в 1749 г. Он же – «батарея», «конденсатор», «проводник», «заряд», «разряд», «обмотка».
Слайд 6
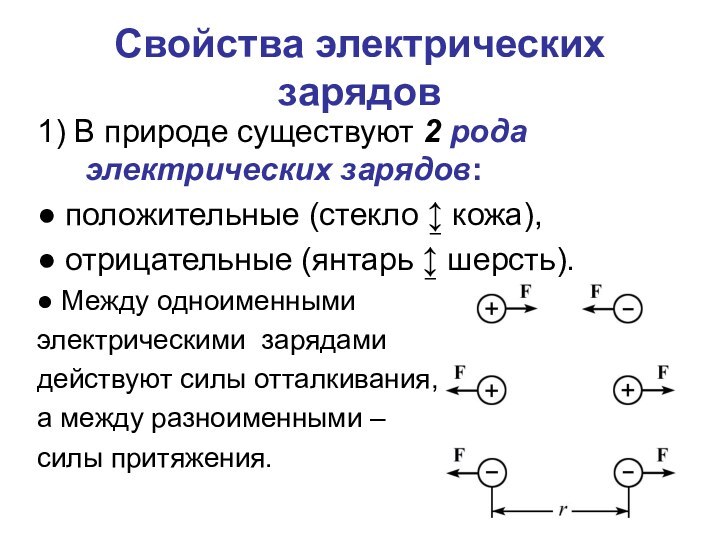
Свойства электрических зарядов
1) В природе существуют 2 рода
электрических зарядов:
● положительные (стекло ↨ кожа),
● отрицательные (янтарь ↨
шерсть).
● Между одноименными
электрическими зарядами
действуют силы отталкивания,
а между разноименными –
силы притяжения.
Слайд 7
Выбор наименований зарядов исторически случаен. Безусловный смысл имеет
только различие знаков заряда. Законы не изменились бы, если
бы положительные заряды переименовали в отрицательные и наоборот: законы взаимодействия зарядов симметричны к замене
+ q на – q.
Слайд 8
Фундаментальное свойство – наличие зарядов в двух видах
– то, что заряды одного знака отталкиваются, а противоположного
– притягиваются. Причина этого современной теорией не объяснена. Существует мнение, что положительные и отрицательные заряды – это противоположное проявление одного качества.
Слайд 9
Свойства электрических зарядов
2) Закон сохранения заряда – фундаментальный
закон (экспериментально подтвержден Фарадеем в 1845 г.)
Полный электрический заряд
изолированной системы есть величина постоянная.
Полный электрический заряд – сумма положительных и отрицательных зарядов, составляющих систему.
Под изолированной в электрическом поле системой понимают систему, через границы которой не может пройти никакое вещество, кроме света.
Слайд 10
В соответствии с законом сохранения заряда разноименные заряды
рождаются и исчезают попарно: сколько родилось (исчезло) положительных зарядов,
столько родилось (исчезло) отрицательных зарядов. Два элементарных заряда противоположных знаков в соответствии с законом сохранения заряда всегда рождаются и исчезают одновременно.
Пример: электрон и позитрон, встречаясь друг с другом, аннигилируют, рождая два или более гамма-фотонов.
e – + e + ? 2γ.
Слайд 11
Свет может входить и выходить из системы, не
нарушая закона сохранения заряда, так как фотон не имеет
заряда; при фотоэффекте возникают равные по величине положительные и отрицательные заряды, а фотон исчезает.
И наоборот, гамма-фотон, попадая в поле атомного ядра, превращается в пару частиц – электрон и позитрон.
γ ? e – + e +.
Слайд 12
Свойства электрических зарядов
3) Электрический заряд – инвариант,
его величина
не зависит от выбора системы отсчета.
Электрический заряд – величина
релятивистки инвариантная,
не зависит от того движется заряд или покоится.
5) Квантование заряда, электрический заряд дискретен, его величина изменяется скачком.
Опыт Милликена (1910 – 1914 гг.)
q = ± n⋅e, где n − целое число. Заряд любого тела составляет целое кратное от элементарного электрического заряда
е = 1,6⋅10−19 Кл (Кулон).
Слайд 13
Суммарный заряд элементарных частиц, если частица им обладает,
равен элементарному заряду.
● Наименьшая частица, обладающая отрицательным элементарным электрическим
зарядом, – электрон, me= 9,11·10-31 кг,
● Наименьшая частица, обладающая положительным элементарным электрическим зарядом, – позитрон, mр= 1,67·10-27 кг. Таким же зарядом обладает протон, входящий в состав ядра.
Равенство зарядов электрона и протона справедливо с точностью до одной части на 1020. То есть фантастическая степень точности. Причина неясна.
Слайд 14
Более точно: установлено, что элементарные частицы представляют собой
комбинацию частиц с дробным зарядом – кварков, имеющих заряды
и .
В свободном состоянии кварки не обнаружены.
Слайд 15
Свойства электрических зарядов
6) Различные тела в классической физике
в зависимости от концентрации свободных зарядов делятся на
● проводники
(электрические заряды могут перемещаться по всему их объему),
● диэлектрики (практически отсутствуют свободные электрические заряды, содержит только связанные заряды, входящие в состав атомов и молекул),
● полупроводники (по электропроводящим свойствам занимают промежуточное положение между проводниками и диэлектриками).
Слайд 16
Свойства электрических зарядов
Проводники делятся на две группы:
1) проводники
первого рода (металлы), в которых перенос зарядов (свободных электронов)
не сопровождается химическими превращениями,
2) проводники второго рода (растворы солей, кислот), перенос зарядов (+ и − ионов) в них сопровождается химическими изменениями.
Слайд 17
Свойства электрических зарядов
7) Единица электрического заряда в
СИ
[1 Кл] – электрический заряд, проходящий через поперечное сечение
проводника при силе тока 1 А за время 1 с.
q = I·t.
Слайд 18
Закон Кулона –
основной закон электростатики
Описывает взаимодействие точечных
зарядов.
Точечный заряд сосредоточен на теле, линейные размеры которого пренебрежимо
малы по сравнению с расстоянием до других заряженных тел.
Точечный заряд, как физическая модель, играет в электростатике ту же роль, что и материальная точка и абсолютно твердое тело в механике, идеальный газ в молекулярной физике, равновесные процессы и состояния в термодинамике.
Закон впервые был открыт в 1772 г. Кавендишем.
Слайд 19
Закон Кулона
В 1785 г. Шарль Огюстен Кулон
экспериментальным путем с помощью крутильных весов определил:
сила взаимодействия F
двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов q1, q2 и обратно пропорциональна квадрату расстояния r между ними
k – коэффициент пропорциональности,
зависящий от выбранной системы единиц.
Слайд 20
Закон Кулона
В опытах определялся вращающий момент:
Сам
Кавендиш, работы которого остались неизвестными, еще в 1770 г.
получил «закон Кулона» с большей точностью.
Слайд 21
Закон Кулона
Сила направлена по прямой,
соединяющей взаимодействующие заряды.
Кулоновская сила является центральной силой.
Слайд 22
Закон Кулона в векторном виде
Сила – величина векторная.
Поэтому запишем закон Кулона в векторном виде.
1) Для произвольно выбранного начала отсчета.
Слайд 23
Закон Кулона в векторном виде
2) Начало отсчета совпадает
с одним из зарядов.
Слайд 24
Закон Кулона
Закон Кулона выполняется при расстояниях 10-15 м
< r < 4·104 км.
В системе СИ: k =
= 9·109
[ м / Ф].
В системе СГС: k = 1.
ε0 = 8,85·10-12 ,[Ф / м] – электрическая постоянная.
Слайд 25
Электрическое поле.
Напряженность электрического поля
Поле – форма материи, обуславливающая
взаимодействие частиц вещества.
Электрическое поле – особая форма существования материи,
посредством которого взаимодействуют электрические заряды.
Электростатическое поле - поле, посредством которого осуществляется кулоновское взаимодействие неподвижных электрических зарядов.
Является частным случаем электромагнитного поля.
Слайд 26
Пробный точечный положительный заряд q0
используют для обнаружения
и исследования электростатического поля.
q0 не вызывает заметного перераспределения зарядов
на телах, создающих поле.
Силовая характеристика электростатического поля определяет, с какой силой поле действует на единичный положительный точечный заряд q0. Такой характеристикой является напряженность электростатического поля.
Слайд 27
Напряженность электрического поля – физическая величина, определяемая силой,
действующей на пробный точечный положительный заряд q0, помещенный в
эту точку поля.
q – источник поля.
q0+ – пробный заряд.
Слайд 28
Напряженность электростатического поля в данной точке численно равна
силе, действующей на единичный положительный точечный заряд, помещенный в
данную точку поля.
Слайд 29
Зная напряженность поля в какой-либо точке пространства, можно
найти силу, действующую на заряд , помещенный в эту
точку:
Это другой вид закона Кулона, который и вводит понятие электрического поля, создающееся зарядами во всем окружающем пространстве,
а также представляет закон действия данного поля на любой заряд.
Слайд 30
Напряженность поля точечного заряда в вакууме.
q – источник
поля,
q0+ – пробный заряд.
Слайд 31
Напряженность электрического поля
E совпадает с направлением силы F,
действующей на пробный заряд q0+ .
Поле создается положительным зарядом
– вектор напряженности электрического поля E направлен от заряда.
Поле создается отрицательным зарядом – вектор напряженности электрического поля E направлен к заряду.
Слайд 32
Напряженность электрического поля
СИ: E измеряется в [1 Н
/Кл = 1 В/м] – это напряженность такого поля, которое на
точечный заряд 1 Кл действует с силой 1 Н.
Слайд 33
Принцип суперпозиции напряженности электрического поля
Опытно установлено, что взаимодействие
двух зарядов не зависит от присутствия других зарядов.
В соответствии
с принципом независимости действия сил: на пробный заряд, помещенный в некоторую точку, будет действовать сила F со стороны всех зарядов qi, равная векторной сумме сил Fi, действующих на него со стороны каждого из зарядов.
Слайд 34
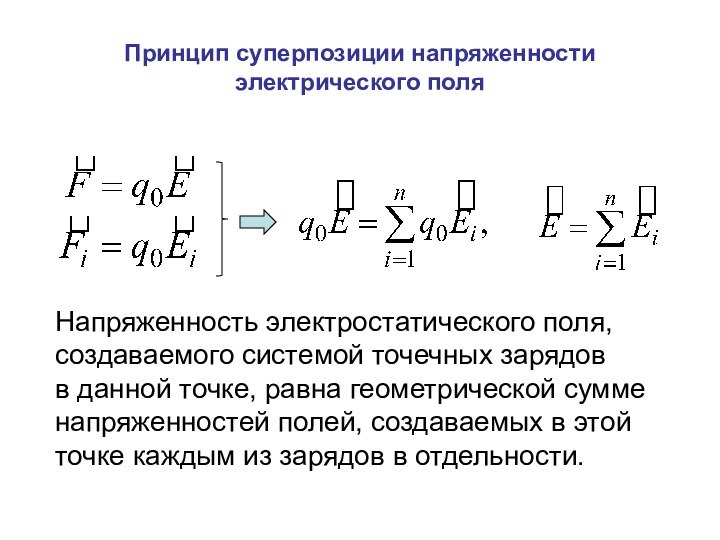
Принцип суперпозиции напряженности электрического поля
Напряженность электростатического поля,
создаваемого
системой точечных зарядов
в данной точке, равна геометрической сумме
напряженностей полей, создаваемых в этой
точке каждым из зарядов в отдельности.
Слайд 35
Первый способ определения напряженности электрического поля Е –
с помощью закона Кулона и принципа суперпозиции.
Поле электрического диполя
Слайд 36
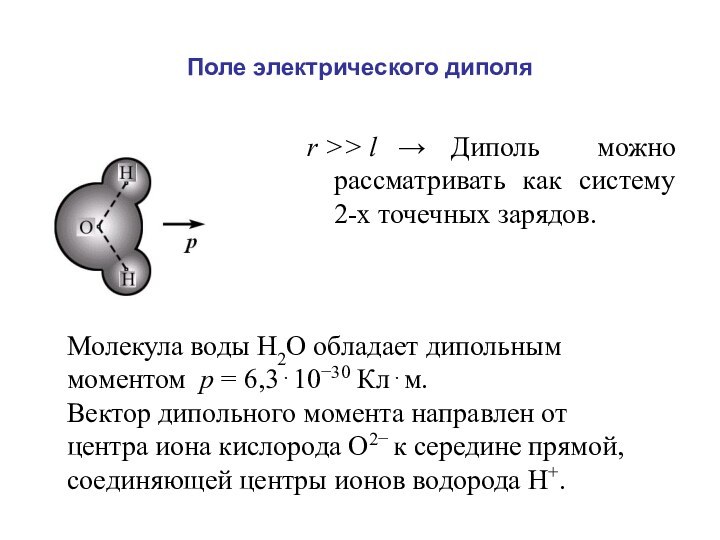
Поле электрического диполя
Электрический диполь - система двух одинаковых
по величине разноименных точечных зарядов, расстояние l между которыми
значительно меньше расстояния до тех точек, в которых определяется поле.
Ось диполя прямая, проходящая через оба заряда.
l – плечо диполя – вектор,
проведенный от отрицательного
заряда к положительному.
Дипольный момент:
Слайд 37
Поле электрического диполя
r >> l → Диполь можно рассматривать как
систему 2-х точечных зарядов.
Молекула воды Н2О обладает дипольным
моментом р = 6,3⋅10−30 Кл⋅м.
Вектор дипольного момента направлен от центра иона кислорода О2− к середине прямой, соединяющей центры ионов водорода Н+.
Слайд 38
Напряженность поля в точке, расположенной на оси диполя.
E1
– напряженность поля положительного заряда.
E2 – напряженность поля отрицательного
заряда.
В проекциях на ось x: E = E1 – E2
Слайд 39
Напряженность поля в точке, расположенной на оси диполя.
Слайд 40
Напряженность поля в точке, расположенной на оси диполя.
Поле
диполя убывает быстрее в зависимости от расстояния по сравнению
с полем точечного заряда.
Слайд 41
Напряженность поля диполя в точке, лежащей на перпендикуляре,
восстановленном к его середине
Слайд 42
Напряженность поля диполя в точке, лежащей на перпендикуляре,
восстановленном к его середине
Уравнения (3),(4), (6)→(5):
Слайд 43
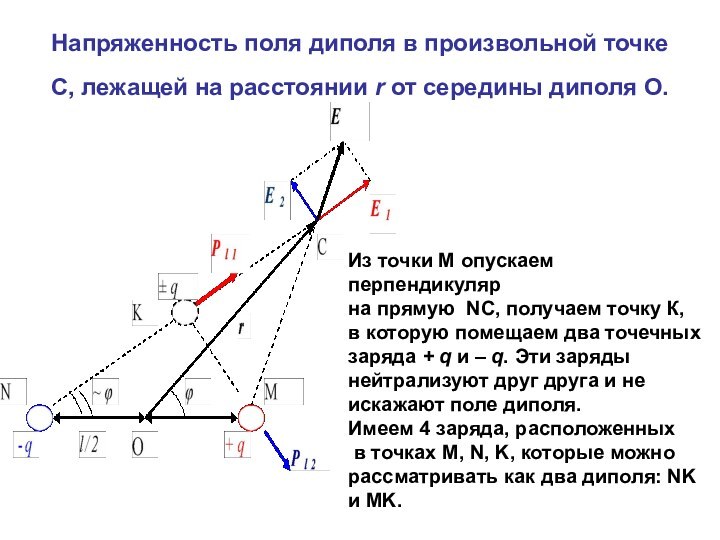
Напряженность поля диполя в произвольной точке С, лежащей
на расстоянии r от середины диполя О.
Из точки
М опускаем перпендикуляр
на прямую NC, получаем точку К,
в которую помещаем два точечных
заряда + q и – q. Эти заряды
нейтрализуют друг друга и не
искажают поле диполя.
Имеем 4 заряда, расположенных
в точках M, N, K, которые можно
рассматривать как два диполя: NK и MK.
Слайд 44
Напряженность поля диполя в произвольной точке С, лежащей
на расстоянии r от середины диполя О.
l
→Угол СNM ≈ φ →
• Электрический момент диполя NK:
• Электрический момент диполя MK:
Слайд 45
Для диполя NK точка С лежит на его
оси
Для диполя МК точка С лежит на перпендикуляре
Слайд 47
В предельных случаях:
а) если , то есть точка
лежит на оси диполя, то получим
б) если ,
то есть точка лежит на перпендикуляре к оси диполя, то получим
Слайд 48
Линейная, поверхностная и объемная плотности зарядов
Хотя электрический заряд
дискретен, число его носителей в макроскопических телах столь велико,
что можно ввести понятие плотности заряда, использовав представление о непрерывном «размазанном» распределении заряда в пространстве.
Слайд 49
Линейная
плотность заряда:
заряд, приходящийся на единицу длины.
Поверхностная
плотность заряда:
заряд, приходящийся на единицу площади.
Объемная
плотность
заряда:
заряд, приходящийся на единицу объема.















![Раздел Электричество Свойства электрических зарядов7) Единица электрического заряда в СИ [1 Кл] – электрический](/img/tmb/12/1160122/30142ade54116041da1a16e4a12a8104-720x.jpg)














![Раздел Электричество Напряженность электрического поляСИ: E измеряется в [1 Н /Кл = 1 В/м] – это](/img/tmb/12/1160122/7335c019adaa89ab236eb2bdcf664378-720x.jpg)