Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Приложения определенного интеграла к решению физических задач

Содержание

2. Цель урока Познакомиться с историей
3. Вычисление площади криволинейной трапецииНа отрезке функция
4. Вычисление объемов тел с помощью определенного интеграла.
5. Вычисление путиПеремещение точки, движущейся по прямой со
6. Вычисление массы неоднородного стержня и координаты центра
7. Интеграл
8. БЕРНУЛЛИ ЯкобСлово интеграл Внес существенный вклад в
9. БЕРНУЛЛИ ИоганнВ 1697 опубликовал работу по экспоненциальному
10. ЛЕЙБНИЦ Готфрид ФридрихНаряду с Ньютоном и
11. Доказал теорему о числе действительных корней алгебраического
12. КЕПЛЕР ИоганнВ своих сочинениях «Новая астрономия» и «Стереометрия винных бочек» правильно вычислил ряд площадей и объемов.
13. Барроу ИсаакОставил способы изучения криволинейных фигур и
14. НЬЮТОН ИсаакОдновременно с Г. Лейбницем, но независимо
15. БУНЯКОВСКИЙ ВикторСделал перевод сочинений Коши о дифференциальном
16. ОСТРОГРАДСКИЙ МихаилМетод выделения рациональной части неопределенного интеграла от рациональной дроби
17. ЧЕБЫШЕВ Пафнутий ЛьвовичПо интегральному исчислению особенно
18. РИМАН БердхардПредложил исследовать внутреннюю геометрию пространств, тем
19. Вычисление площади криволинейной трапецииНа отрезке функция
20. Вычисление объемов тел с помощью определенного интеграла.
21. Вычисление путиПеремещение точки, движущейся по прямой со
22. Вычисление массы неоднородного стержня и координаты центра
23. Работа переменной силыПусть точка движется по оси
24. Работа переменной силыРазобьём отрезок [a;b] на n
25. Работа переменной силыЗначит, работа силы на всем
26. Этапы работы над задачейИсследовать физическую ситуациюПеревести содержание
27. Задача 1Нефть, подаваемая в цилиндрическийбак через отверстие
28. Задача 2 Канал имеет в разрезе
29. Задача 3Вычислите работу, которую необходимо совершить, чтобы
30. Слово интеграл от латинского integer – целый.
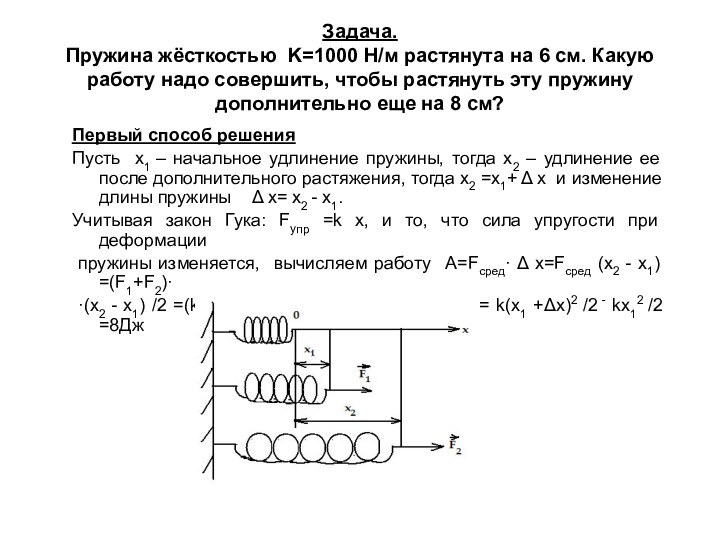
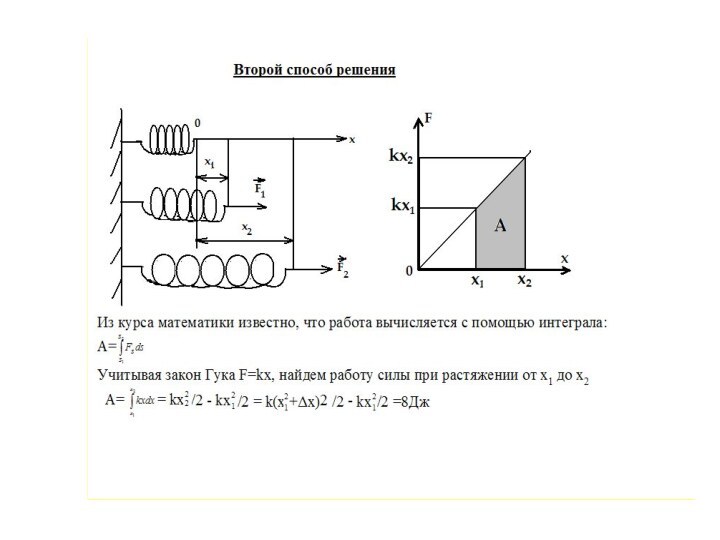
31. Задача. Пружина жёсткостью K=1000 Н/м растянута
32. Скачать презентацию
33. Похожие презентации

Цель урока Познакомиться с историей развития интегрального и дифференциального исчисленияНаучиться применять интеграл для решения физических задач

Главная
Физика
Приложения определенного интеграла к решению физических задач

Тема урокаПриложения определенного интеграла к решению физических задач

Цель урока Познакомиться с историей развития интегрального и дифференциального исчисленияНаучиться

Вычисление площади криволинейной трапецииНа отрезке функция

Вычисление объемов тел с помощью определенного интеграла.

Вычисление путиПеремещение точки, движущейся по прямой со скоростью v = v (t),

Вычисление массы неоднородного стержня и координаты центра масса) суммарная масса М стержня

БЕРНУЛЛИ ЯкобСлово интеграл Внес существенный вклад в разработку основ дифференциального и интегрального

БЕРНУЛЛИ ИоганнВ 1697 опубликовал работу по экспоненциальному исчислению, в которой впервые сформулировал

ЛЕЙБНИЦ Готфрид ФридрихНаряду с Ньютоном и независимо от него, создал дифференциальное

Доказал теорему о числе действительных корней алгебраического уравнения, лежащих между данными пределами

КЕПЛЕР ИоганнВ своих сочинениях «Новая астрономия» и «Стереометрия винных бочек» правильно вычислил ряд площадей и объемов.

Барроу ИсаакОставил способы изучения криволинейных фигур и метод касательных, в чём многие

НЬЮТОН ИсаакОдновременно с Г. Лейбницем, но независимо от него, создал дифференциальное и

БУНЯКОВСКИЙ ВикторСделал перевод сочинений Коши о дифференциальном и интегральном исчислениях, причём присоединил

ОСТРОГРАДСКИЙ МихаилМетод выделения рациональной части неопределенного интеграла от рациональной дроби

ЧЕБЫШЕВ Пафнутий ЛьвовичПо интегральному исчислению особенно замечателен мемуар 1860 г.: «Sur

РИМАН БердхардПредложил исследовать внутреннюю геометрию пространств, тем самым заложил основы дифференциальной геометрии

Работа переменной силыПусть точка движется по оси Ох под действием силы, проекция

Работа переменной силыРазобьём отрезок [a;b] на n отрезков одинаковой длиныТ. к. f

Работа переменной силыЗначит, работа силы на всем отрезке Приближенное равенство переходит в

Этапы работы над задачейИсследовать физическую ситуациюПеревести содержание задачи на язык функцийПрименить математические

Задача 1Нефть, подаваемая в цилиндрическийбак через отверстие в дне, заполняетвесь бак. Определите

Задача 2 Канал имеет в разрезе форму равнобедренной трапеции высотой h

Задача 3Вычислите работу, которую необходимо совершить, чтобы поднять тело массой m с

Слово интеграл от латинского integer – целый. Интеграция – восстановление, восполнение, воссоединение.

Задача. Пружина жёсткостью K=1000 Н/м растянута на 6 см. Какую работу

Приложения определенного интеграла к решению физических задач

Слайды презентации

Слайд 2 Цель урока
Познакомиться с историей развития интегрального и дифференциального

исчисления
Научиться применять интеграл для решения физических задач

Слайд 3 Вычисление площади криволинейной трапеции
На отрезке

функция

Слайд 4 Вычисление объемов тел с помощью
определенного интеграла.

Слайд 5 Вычисление пути
Перемещение точки, движущейся по прямой со скоростью

Вычисление путиПеремещение точки, движущейся по прямой со скоростью v = v

v = v (t), за промежуток времени

, вычисляется по формуле

Слайд 6 Вычисление массы неоднородного стержня и координаты центра масс
а)

Вычисление массы неоднородного стержня и координаты центра масса) суммарная масса М

суммарная масса М стержня равна

в) координата центра масс равна

Слайд 7 Интеграл

Слайд 8 БЕРНУЛЛИ Якоб
Слово интеграл
Внес существенный вклад в разработку

БЕРНУЛЛИ ЯкобСлово интеграл Внес существенный вклад в разработку основ дифференциального и

основ дифференциального и интегрального исчислений, аналитической геометрии, теории вероятностей

и вариационного исчисления. Решил проблему Лейбница об изохронной кривой, исследовал логарифмическую спираль, ввел полярные координаты.

Слайд 9 БЕРНУЛЛИ Иоганн
В 1697 опубликовал работу по экспоненциальному исчислению,

БЕРНУЛЛИ ИоганнВ 1697 опубликовал работу по экспоненциальному исчислению, в которой впервые

в которой впервые сформулировал задачу о брахистохроне;
Ряд открытий

в области интегрального и дифференциального исчислений.

Слайд 10 ЛЕЙБНИЦ Готфрид Фридрих
Наряду с Ньютоном и независимо от

него, создал дифференциальное и интегральное исчисления.
Ввёл применяемое и сегодня

обозначение производной df/dx.
Ввёл бинарную систему счисления с цифрами 0 и 1, на котором базируется современная компьютерная техника.

Слайд 11 Доказал теорему о числе действительных корней алгебраического уравнения,

Доказал теорему о числе действительных корней алгебраического уравнения, лежащих между данными

лежащих между данными пределами
Нашел формулу представления функции с

помощью интеграла, играющую важную роль в современной математике.
Доказал, что всякую произвольно начерченную линию, составленную из отрезков дуг разных кривых, можно представить единым аналитическим выражением.

Фурье

Слайд 12 КЕПЛЕР Иоганн
В своих сочинениях «Новая астрономия» и «Стереометрия

винных бочек» правильно вычислил ряд площадей и объемов.

Слайд 13 Барроу Исаак
Оставил способы изучения криволинейных фигур и метод

Барроу ИсаакОставил способы изучения криволинейных фигур и метод касательных, в чём

касательных, в чём многие видели предвестника дифференциального исчисления.

Слайд 14 НЬЮТОН Исаак
Одновременно с Г. Лейбницем, но независимо от

НЬЮТОН ИсаакОдновременно с Г. Лейбницем, но независимо от него, создал дифференциальное

него, создал дифференциальное и интегральное исчисления.
Вместе с Г.

В. Лейбницем считается основоположником дифференциального исчисления.

Слайд 15 БУНЯКОВСКИЙ Виктор
Сделал перевод сочинений Коши о дифференциальном и

БУНЯКОВСКИЙ ВикторСделал перевод сочинений Коши о дифференциальном и интегральном исчислениях, причём

интегральном исчислениях, причём присоединил к этому переводу свои примечания,

а также составил, по поручению министерства народного просвещения, несколько учебных руководств по разным отраслям математики.

Слайд 16 ОСТРОГРАДСКИЙ Михаил
Метод выделения рациональной части неопределенного интеграла от

рациональной дроби

Слайд 17 ЧЕБЫШЕВ Пафнутий Львович
По интегральному исчислению особенно замечателен мемуар

1860 г.: «Sur l'intégration de la différentielle», в котором

даётся способ узнать при помощи конечного числа действий, в случае рациональных коэффициентов подкоренного полинома, возможно ли определить число А так, чтобы данное выражение интегрировалось в логарифмах и, в случае возможности, найти интеграл.

Слайд 18 РИМАН Бердхард
Предложил исследовать внутреннюю геометрию пространств, тем самым

РИМАН БердхардПредложил исследовать внутреннюю геометрию пространств, тем самым заложил основы дифференциальной

заложил основы дифференциальной геометрии и подготовив фундамент для общей

теории относительности
Рассмотрел формализацию понятия интеграла и ввёл своё определение — интеграл Римана.

Слайд 19 Вычисление площади криволинейной трапеции
На отрезке

функция

Слайд 20 Вычисление объемов тел с помощью
определенного интеграла.

Слайд 21 Вычисление пути
Перемещение точки, движущейся по прямой со скоростью

v = v (t), за промежуток времени

, вычисляется по формуле

Слайд 22 Вычисление массы неоднородного стержня и координаты центра масс
а)

суммарная масса М стержня равна

в) координата центра масс равна

Слайд 23 Работа переменной силы
Пусть точка движется по оси Ох

Работа переменной силыПусть точка движется по оси Ох под действием силы,

под действием силы, проекция которой на ось Ох есть

функция f от x. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М(a) в точку М(b). Покажем, что в этом случае работа А подсчитывается по формуле

Слайд 24 Работа переменной силы
Разобьём отрезок [a;b] на n отрезков

Работа переменной силыРазобьём отрезок [a;b] на n отрезков одинаковой длиныТ. к.

одинаковой длины
Т. к. f (x) – непрерывная функция от

х, при достаточно малом отрезке [a;b] работа силы на этом отрезке приближенно равна f(a)( -a). Т. О. работа силы на n-м отрезке приближенно равна f( )(b - ).

Слайд 25 Работа переменной силы
Значит, работа силы на всем отрезке

Работа переменной силыЗначит, работа силы на всем отрезке Приближенное равенство переходит

Приближенное равенство переходит в точное, если считать , что

n→

Слайд 26 Этапы работы над задачей

Исследовать физическую ситуацию
Перевести содержание задачи

Этапы работы над задачейИсследовать физическую ситуациюПеревести содержание задачи на язык функцийПрименить

на язык функций
Применить математические методы
для решения задачи
Проанализировать полученный

результат

Слайд 27 Задача 1
Нефть, подаваемая в цилиндрический
бак через отверстие в

Задача 1Нефть, подаваемая в цилиндрическийбак через отверстие в дне, заполняетвесь бак.

дне, заполняет
весь бак. Определите затраченную
при этом работу. Высота бака

– h, а
радиус основания R.

Слайд 28 Задача 2
Канал имеет в разрезе форму

равнобедренной трапеции высотой h с основаниями a и b.

Найдите силу, с которой вода, заполняющая канал, давит на плотину.

Слайд 29 Задача 3
Вычислите работу, которую необходимо совершить, чтобы поднять

Задача 3Вычислите работу, которую необходимо совершить, чтобы поднять тело массой m

тело массой m с поверхности Земли на высоту h

Слайд 30 Слово интеграл от латинского integer – целый.

Интеграция

Слово интеграл от латинского integer – целый. Интеграция – восстановление, восполнение,

– восстановление, восполнение, воссоединение.

Интегрирование – процесс объединения отдельных

частей в целое.

Слайд 31 Задача. Пружина жёсткостью K=1000 Н/м растянута на 6

см. Какую работу надо совершить, чтобы растянуть эту пружину

дополнительно еще на 8 см?

Первый способ решения
Пусть х1 – начальное удлинение пружины, тогда х2 – удлинение ее после дополнительного растяжения, тогда х2 =х1+ Δ х и изменение длины пружины Δ х= х2 - х1.
Учитывая закон Гука: Fупр =k х, и то, что сила упругости при деформации
пружины изменяется, вычисляем работу А=Fсред· Δ х=Fсред (x2 - x1) =(F1+F2)·
·(x2 - x1) /2 =(kx1+ kx2)(x2 - x1)/2= kx22/2 - kx12 /2 = k(x1 +Δх)2 /2 - kx12 /2 =8Дж