- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Синтез механизмов
Содержание
- 2. План лекции Проектирование плоских и пространственных механизмов. Синтез
- 3. Проектирование плоских и пространственных механизмов В теории механизмов
- 4. Детали, предназначенные для передачи вращательного движения, укрепляют
- 5. Передача вращательного движения между валами, оси которых
- 6. Передача вращательного движения может производиться с увеличением
- 7. Рис.1а) Передача вращательного движения между валами с параллельными осями.
- 8. Синтез трехзвенных плоских зубчатых механизмов с круглыми
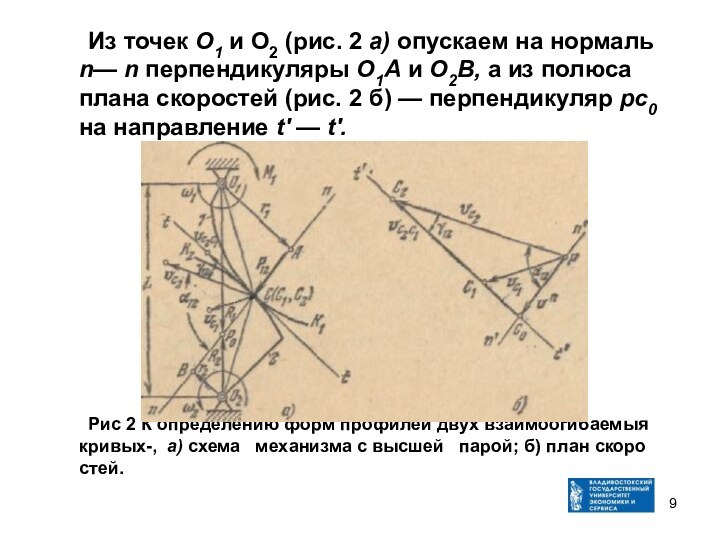
- 9. Из точек О1 и O2 (рис. 2
- 10. Отрезок (рс0) представляет собою нормальную составляющую vn
- 11. Заменяя vс1 , и vс2 их значениями,
- 12. Следовательно, передаточная функция i12 равна(2.3) Продолжим нормаль n
- 13. Эвольвенты и её свойства Эвольвента и ее свойства Эвольвента
- 14. Так как KyNy перекатывается без скольжения по
- 15. Уравнения (1) И (2) являются уравнениями эвольвенты
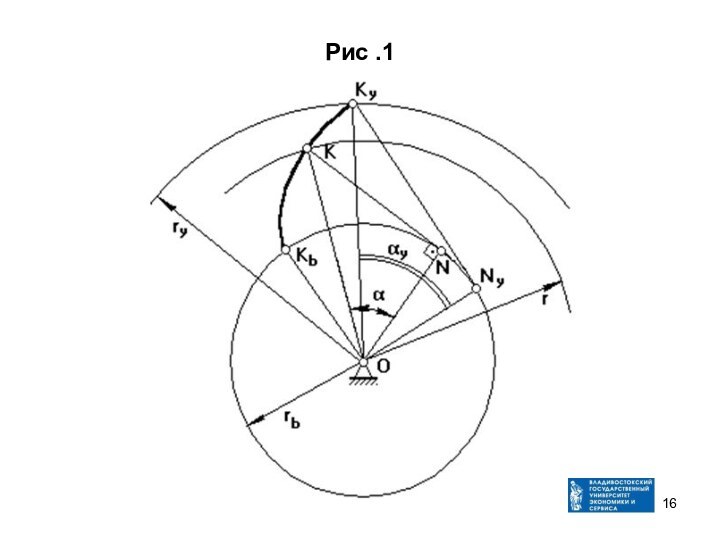
- 16. Рис .1
- 17. Геометрические элементы зубчатых колес Ниже даны
- 18. Геометрия эвольвентных профилей Делительной окружностью называется окружность стандартных
- 19. Модуль характеризует высоту зуба. Чем больше зуб,
- 20. Проектирование эвольвентных профилей Эвольвентную зубчатую передачу составляют, как
- 21. Линия зацепления является геометрическим местом точек контакта
- 22. Угол N1O1P = углу N2J2P = w
- 23. Между делительными окружностями у.m – это воспринимаемое
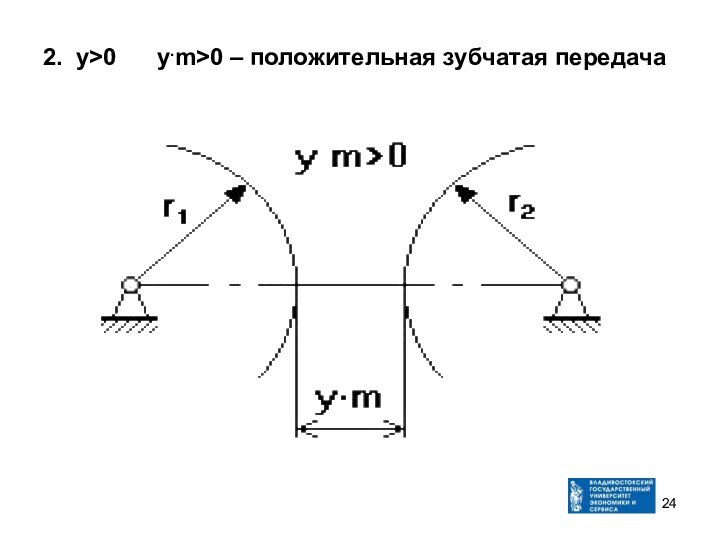
- 24. 2. у>0 у.m>0 – положительная зубчатая передача
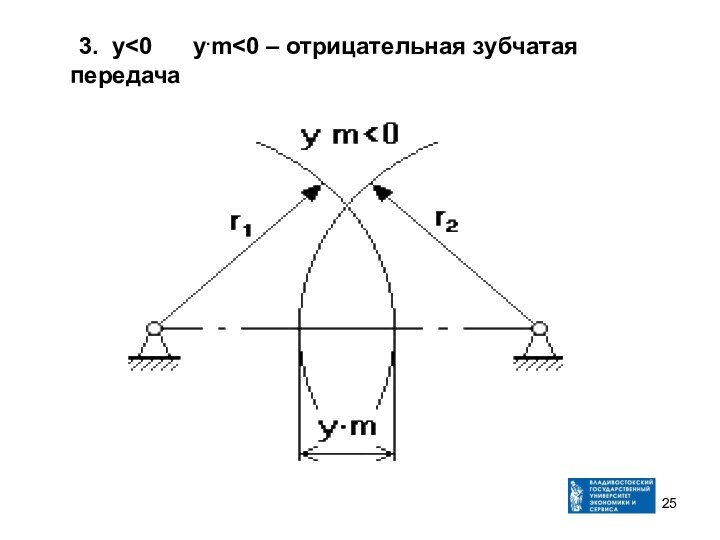
- 25. 3. у
- 26. Свойства эвольвентного зацепления. 1. Эвольвентное зацепление молочувствительно к
- 27. Винтовая передача (винт-гайка) Винтовая передача преобразует вращательное движение в поступательное. Пример винтовой передачи
- 28. Проектирование винтовой передачи ВИНТОВАЯ ПЕРЕДАЧА
- 29. Основы расчета винтовой передачи Параметры резьбы рассчитывают, исходя
- 30. В винтовых механизмах вращение винта или гайки
- 31. При малом рz1 и сравнительно большом D
- 32. Таким образом, при простой и компактной конструкции
- 33. Проектирование червячной передачи Червячная передача имеет перекрещивающиеся оси
- 34. Передаточное отношение червячной передачи находят аналогично цилиндрической
- 35. Рисунок 1 Далее расчёт проводится по формуле Герца-Беляева.
- 36. Скачать презентацию
- 37. Похожие презентации
План лекции Проектирование плоских и пространственных механизмов. Синтез трехзвенных плоских зубчатых механизмов с круглыми цилиндрическими колесами, геометрические элементы зубчатых колес, геометрия эвольвентных профилей, проектирование эвольвентных профилей. Синтез трехзвенных пространственных зубчатых механизмов, проектирование винтовой и червячной передач.































Слайд 3
Проектирование плоских и пространственных механизмов
В теории механизмов и
машин под термином синтез понимают проектирование механизмов. Для этого
сначала формулируют техническое задание, в котором должны быть отражены назначение механизма в соответствии с технологическим процессом или технологическими операциями, функции движения выходных звеньев и функции изменения сил полезных сопротивлений, а также вид источников энергии.Слайд 4 Детали, предназначенные для передачи вращательного движения, укрепляют на
валах, представляющих собой вращающиеся в опорах стержни, в большинстве
случаев цилиндрической формы. Вал, от которого передается движение, называется ведущим; вал, которому передается движение, называется ведомым.Передачу вращательного движения возможно осуществить между валами, расположенными в пространстве как угодно: оси валов могут быть параллельными, пересекаться под любым углом, а также перекрещиваться под любым углом.
Слайд 5 Передача вращательного движения между валами, оси которых параллельны,
осуществляется при помощи плоских механизмов, в остальных случаях —
при помощи пространственных механизмов.Передача вращательного движения производится одним из следующих способов:
непосредственным соприкосновением двух тел, одно из которых связано жестко с ведущим, а другое — с ведомым валом;
посредством гибких тел, сцепляющихся с телами, жестко связанными с ведущим, и ведомым валами.
Слайд 6 Передача вращательного движения может производиться с увеличением или
уменьшением угловой скорости вращения, а также без ее изменения.
Отношение
угловых скоростей вращения обоих валов называется передаточным отношением. Передаточное отношение может быть, следовательно, выражено отношением угловой скорости ведущего вала к угловой скорости ведомого вала или наоборот.Передаточное отношение в направлении силового потока, т. е. отношение угловой скорости ведущего вала к угловой скорости ведомого, называется передаточным числом*.
Слайд 8 Синтез трехзвенных плоских зубчатых механизмов с круглыми цилиндрическими
колесами
(основные сведения из теории зацепления)
Пусть передача вращения между двумя
осями 01 и 02 (рис. 2 а) с угловыми скоростями ω1 и ω2 осуществляется посредством двух взаимоогибаемых кривых К1 и К2, принадлежащих звеньям 1 и 2. Проведем в точке соприкосновения С кривых К1 и К2 нормаль n — n и касательную t — t к этим кривым.Скорости vС1 и vС2 точек С1 и С2, принадлежащих звеньям 1 и 2, связаны условием
vc1=vc1+vc2c1
План скоростей механизма, построенный по этому уравнению, показан на (рис. 2 б)
Слайд 9 Из точек О1 и O2 (рис. 2 а)
опускаем на нормаль n— n перпендикуляры О1А и О2В,
а из полюса плана скоростей (рис. 2 б) — перпендикуляр рс0 на направление t' — t'.Рис 2 К определению форм профилей двух взаимоогибаемыя кривых-, а) схема механизма с высшей парой; б) план скоростей.
Слайд 10 Отрезок (рс0) представляет собою нормальную составляющую vn векторов скоростей
vc1 и vc2
Из подобия треугольников О1АС1 и рс0с1 и
треугольников О2ВС2и рс0с2 имеем
(2.1)
Отрезки (рс1), (рc 2) и (рс0) представляют собой соответственно скорости vС1, vС2 и vn . Тогда соотношения (2.1) могут быть представлены так:
Или
Слайд 11
Заменяя vс1 , и vс2 их значениями, равными
vс1=
ω 1 (O 1 C 1) vс2= ω 2
(O 2 C 2),Получаем
vn= ω 1 (O 1 А) и vn= ω 2 (O 2 B) ,
Откуда
ω 1 (O 1 А) = ω 2 (O 2 B) . (2.2)
Слайд 12
Следовательно, передаточная функция i12 равна
(2.3)
Продолжим нормаль n —
n до пересечения в точке Р0 с отрезком (О1O2).
Тогда из подобия треугольников O1АР0 и O2ВР0 имеемИ формула (2.3) принимает окончательный вид:
(2.4)
Равенство (2.4) называется основной теоремой зацепления.
Слайд 13
Эвольвенты и её свойства
Эвольвента и ее свойства
Эвольвента образуется
путем перекатывания производящей прямой KyNy без скольжения по основной
окружности радиуса rb (рис. 1).Радиус произвольной окружности – ry. ONy ||
Из треугольника ONyKy следует, что
(1)
Слайд 14 Так как KyNy перекатывается без скольжения по основной
окружности, то
(2)
rb(y + y) = rb.tg y
y =
tg y - y y = inv y
y – инволюта;
Слайд 15 Уравнения (1) И (2) являются уравнениями эвольвенты в
параметрической форме.
у – угол профиля эвольвенты для точки Ку,
лежащей на произвольной окружности. – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.
Угол профиля эвольвенты для точки Кb, лежащей на основной окружности, равен нулю: b=0.
Свойства эвольвенты:
1. Форма эвольвенты зависит от радиуса основной окружности.
2. Производящая прямая KyNy является нормалью к эвольвенте в данной тоске.
3. Эвольвента начинается от основной окружности..
Слайд 17
Геометрические элементы зубчатых колес
Ниже даны стандартные
зависимости зубчатых зацеплений, предусмотренные ГОСТ для нормального прямозубого колеса
Шаг
зацепления передачи t = πт
Высота головки зуба h' = mВысота ножки зуба h"= 1,25/72
Высота зуба h = 2,25m
Радиальный зазор е = 0,25m
Диаметр делительной окружности, выраженный в мм, de = тz
Диаметр окружности головок De — m(z -f- 2)
Диаметр окружности ножек Di=m(z— 2,5)
Слайд 18
Геометрия эвольвентных профилей
Делительной окружностью называется окружность стандартных шага
р, модуля m и угла профиля .
Шаг – расстояние
между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:
1 ряд – наиболее предпочтительный;
2 ряд – средней предпочтительности;
3 ряд – наименее предпочтительный.
Слайд 19 Модуль характеризует высоту зуба. Чем больше зуб, тем
более шумной становится зубчатая передача.
Угол профиля – угол
между касательной к эвольвенте в данной точке и радиус-вектором данной точки.Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20о (хотя лучше 25о).
Основные расчетные зависимости:
Радиус делительной окружности
rb=r cosα; α = p cos20°
Модуль по ГОСТ
Слайд 20
Проектирование эвольвентных профилей
Эвольвентную зубчатую передачу составляют, как минимум,
из 2-х зубчатых колес, при этом в рассмотрение вводится
две начальные окружности радиусами rw1 и rw2.Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.
Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N1N2, которая одновременно касается 2-х основных окружностей rb1 и rb2.
Слайд 21 Линия зацепления является геометрическим местом точек контакта сопряженных
эвольвентных профилей.
В точке В1 пара эвольвент, которые в
данный момент времени контактируют в точке К, входят в зацепление. В точке В2 этаже пара эвольвент из зацепления выходят.На линии зацепления N1N2 все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N1N2 эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.
Слайд 22 Угол N1O1P = углу N2J2P = w –
угол зацепления.
Для передачи, составленной из нулевых зубчатых колес
w=20oДля передачи, составленной из положительных з. к. w>20o
Для передачи, составленной из отрицательных з. к. w<20o
c=c*.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.
c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).
Слайд 23
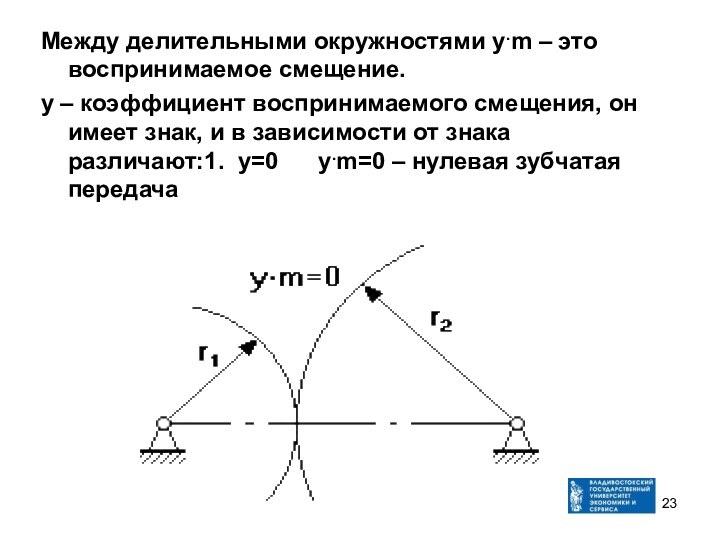
Между делительными окружностями у.m – это воспринимаемое смещение.
у
– коэффициент воспринимаемого смещения, он имеет знак, и в
зависимости от знака различают:1. у=0 у.m=0 – нулевая зубчатая передача
Слайд 26
Свойства эвольвентного зацепления.
1. Эвольвентное зацепление молочувствительно к погрешностям
изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное
отношение зубчатой передачи не изменится.2. Линия зацепления N1N2 является общей нормалью к сопряженным эвольвентным профилям.
3. Контакт эвольвент осуществляется только на линии зацепления.
Слайд 27
Винтовая передача
(винт-гайка)
Винтовая передача преобразует вращательное
движение в поступательное.
Пример винтовой передачи
Слайд 28
Проектирование винтовой передачи
ВИНТОВАЯ ПЕРЕДАЧА —
устройство, содержащее винтовую пару, у которой гайка и винт
образуют кинематические пары со стойкой или звеньями другого механизма. Причем в первом случае. Винтовая передача также называется передачей «винт—гайка».
Слайд 29
Основы расчета винтовой передачи
Параметры резьбы рассчитывают, исходя из
заданных скоростей и нагрузок на выходном звене.
Относительное перемещение гайки
и винта (ход резьбы рг) определяют в зависимости от скорости поступательного движения v и угловой скорости со винта или гайки:pz = 2πv/ω
где v — мм/с; ω — рад/с.
Слайд 30 В винтовых механизмах вращение винта или гайки осуществляется,
как правило, с помощью маховичка, шестерни и т. п.
При этом условное передаточное отношение можно выразить отношением перемещения маховичка SМ к перемещению гайки (винта)i = Sм/Sг=πD/pz,
где D —диаметр маховичка (шестерни и т. п.), pz1— ход винта.
Слайд 31 При малом рz1 и сравнительно большом D можно
получить очень большое i. Например, при рz1 = 1
мм,D = 100 мм, i = 314.
Зависимость между окружной силой Ftм на маховичке и осевой силой Fa на гайке (винте) имеет вид
Fa=Ftмiη,
где η— к. п. д. винтовой - пары.
Для i = 314 и η ≈0,3 Fa ≈ 95 Ftм
Слайд 32 Таким образом, при простой и компактной конструкции передача
винт—гайка позволяет получить большой выигрыш в силе или осуществлять
медленные и точные перемещения.-Соотношение между крутящим моментом Мк на гайке и осевой силой F a на винте имеет вид
MK = Fa d2/2 tg(γ + ρ),
где ρ — угол трения (в расчетах принимается ρ ≈ 6°, что соответствует коэффициенту трения f ≈0,1).
Слайд 33
Проектирование червячной передачи
Червячная передача имеет перекрещивающиеся оси валов,
обычно под углом 90. Она состоит из червяка –
винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы. Движение в червячной передаче преобразуется по принципу винтовой пары. Изобретателем червячных передач считают Архимеда.
Слайд 34
Передаточное отношение червячной передачи находят аналогично цилиндрической
U
= n1 / n2 = Z2 / Z1.
Здесь Z2
– число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.В осевом сечении червячная пара (рис .1) фактически представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности "рейки" (винта червяка) 1 равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса пр = 2.
Слайд 35
Рисунок 1
Далее расчёт проводится по формуле Герца-Беляева. Из
проектировочного расчёта находят осевой модуль червяка, а по нему
и все геометрические параметры зацепления.Особенность расчёта на изгиб состоит в том, что принимается эквивалентное число зубьев Zэкв = Z2 / cos3, где - угол подъёма витков червяка.





























