- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Скорость движения
Содержание
- 2. 2.3. Кинематика поступательного движения Рассмотрим движение материальной точки
- 3. 2.3. Кинематика поступательного движенияМодель: Движение тела в поле тяжести ЗемлиСодержание
- 4. Пусть материальная точка
- 5. Мгновенная скорость – векторная величина, равная скорости
- 6. Так как секущая в
- 7. При неравномерном движении модуль
- 8. В случае равномерного
- 9. В случае неравномерного
- 10. Перенесем вектор в точку А и
- 11. Тангенциальная составляющая ускореният.е. равна первой производной по
- 12. В пределе при ∆t→0 получим
- 13. Полное ускорение тела есть геометрическая сумма тангенциальной
- 14. В зависимости от тангенциальной и нормальной составляющих
- 15. 3. aτ = f(t), an = 0
- 16. 5. aτ = 0, an ≠ 0
- 17. ЗадачиМаленький шарик начинает скатываться без начальной скорости
- 18. Лекция окончена!
- 19. Движение в поле тяжести ЗемлиРассмотрим движение свободного
- 20. Скачать презентацию
- 21. Похожие презентации



















Слайд 3
2.3. Кинематика поступательного движения
Модель: Движение тела в поле
тяжести Земли
Содержание
Слайд 4 Пусть материальная точка движется
по какой–либо криволинейной траектории так, что в момент времени
t ей соответствует радиус–вектор . В течение малого промежутка времени точка пройдет путь ∆S и получит элементарное (бесконечно малое ) перемещение Вектором средней скорости < > называется приращение радиус–вектора точки к промежутку времени Δt :
(2.3)
2.4. Скорость
Слайд 5
Мгновенная скорость – векторная величина, равная скорости материальной
точки в фиксированный момент времени.
Мгновенная скорость – векторная величина,
равная первой производной радиус–вектора движущейся точки по времени.2.4. Скорость
Слайд 6 Так как секущая в пределе
совпадает с касательной, то вектор скорости направлен по касательной
к траектории в сторону движения, поэтому модуль мгновенной скоростиТаким образом, модуль мгновенной скорости равен первой производной пути по времени
(2.4)
2.4. Скорость
Слайд 7 При неравномерном движении модуль мгновенной
скорости с течением времени изменяется. В данном случае пользуются
скалярной величиной <υ> – средней скоростью неравномерного движения . Из рис. 3 вытекает, что , так как , и только в случае прямолинейного движения .Если выражение ds=υdt (см. формулу 2.4) проинтегрировать по времени в пределах от t до t+∆t, то найдем длину пути, пройденного точкой за время ∆t:
(2.5)
2.4. Скорость
Слайд 8
В случае равномерного движения
числовое значение мгновенной скорости постоянно; тогда выражение (2.5) примет
вид:Длина пути, пройденного точкой за промежуток времени от t1 до t2 дается интегралом:
2.4. Скорость
Содержание
Слайд 9 В случае неравномерного движения
важно знать, как быстро изменяется скорость с течением времени.
Физической величиной характеризующей быстроту изменения скорости по модулю и направлению является ускорение.Рассмотрим плоское движение, то есть движение, при котором все участки траектории точки лежат в одной плоскости.
Пусть вектор задает скорость точки А в момент времени t. За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от как по модулю, так и по направлению и равную
2.5. Ускорение и его составляющие.
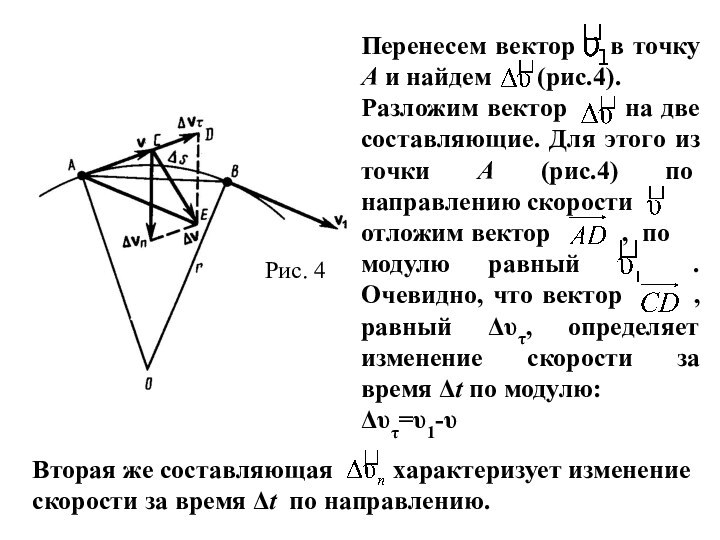
Слайд 10 Перенесем вектор в точку А и найдем
(рис.4).
Разложим вектор на
две составляющие. Для этого из точки А (рис.4) по направлению скорости отложим вектор , по
модулю равный . Очевидно, что вектор , равный Δυτ, определяет изменение скорости за время Δt по модулю:
Δυτ=υ1-υ
Рис. 4
Вторая же составляющая характеризует изменение скорости за время Δt по направлению.
Слайд 11
Тангенциальная составляющая ускорения
т.е. равна первой производной по времени
от модуля скорости, определяя тем самым быстроту изменения скорости
по модулю. Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому можно считать дугу окружности радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и ЕАД следует Δυn /AB= Δυ1 /r, но т.к. AB = υ·Δt , то
Слайд 12 В пределе при ∆t→0 получим
.
Поскольку
, угол ЕАD стремится к нулю, и т.к. треугольник ЕАD равнобедренный, то угол АDЕ междуи стремится к прямому. Следовательно, при ∆t→0 векторы и оказываются взаимно перпен-дикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения равная
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Слайд 13 Полное ускорение тела есть геометрическая сумма тангенциальной и
нормальной составляющих:
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости
по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения – быстроту изменения скорости по направлению (направлена к центру кривизны траектории).Слайд 14 В зависимости от тангенциальной и нормальной составляющих ускорения
движение можно классифицировать следующим образом:
1. aτ = 0, an=
0 – прямолинейное равномерное движение;2. aτ = a = const, an = 0 – прямолинейное
равнопеременное движение.
При таком виде движения .
Если начальный момент времени t1=0 , а начальная скорость υ1 =υ0, то, обозначив t2= t и υ2 =υ, получим a = (υ - υ0)/t, откуда
Слайд 15 3. aτ = f(t), an = 0 –
прямолинейное движение с
переменным ускорением. 4. aτ = 0, an=const.
При aτ = 0 скорость по модулю не меняется, а изменяется по направлению. Из формулы an= υ2/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным.
Проинтегрировав эту формулу в пределах от нуля до произвольного момента t, найдем, что длина пути пройденного точкой, в случае равнопеременного движения
Слайд 16 5. aτ = 0, an ≠ 0 –
равномерное криволинейное движение.
6. aτ = const, an ≠ 0 – криволинейное равнопеременное
движение.
7. aτ = f(t), an ≠ 0 - криволинейное движение
с переменным ускорением.
Содержание
Слайд 17
Задачи
Маленький шарик начинает скатываться без начальной скорости с
вершины абсолютно гладкой полусферы радиуса R. На какой высоте
он оторвётся от поверхности. Ответ: 2R/3Цилиндр радиуса R лежит на двух тонких стержнях. С какой относительной скоростью V должны раздвигаться стержни, чтобы падения цилиндра происходило без контакта с ними. Ответ:
С какой скоростью шарик должен двигаться по верхней ступени лестницы, чтобы удариться о среднюю и нижнюю ступень только по одному разу. Ширина и высота ступеней - b. Ответ:
Слайд 19
Движение в поле тяжести Земли
Рассмотрим движение свободного тела
в присутствии гравитационного поля Земли на примере выстрела из
пушки. Если пушка расположена в точке с коорди-натами (0, 0, 0), то снаряд будет двигаться по траектории, которая описывается следующими уравнениями:X=(υcosϕ)t
Y = (υsinϕ)t - gt2/2,
где υ - скорость снаряда вдоль ствола пушки, ϕ - угол между стволом пушки и горизонтом (ось X), t - время, g - ускорение свободного падения в поле тяжести Земли. Подставляя t из первого уравнения во второе, находим уравнение траектории движения снаряда:
Y = X tg ϕ - (g/2 υ 2)(1 + tg2 ϕ) X2
Дальше





























