электронной теории. Работы в области электродинамики, термодинамики, оптики, теории
излучения, атомной физики.
Исходя из электромагнитной теории Максвелла–Герца и вводя в учение об электричестве атомистику, создал (1880–1909) классическую электронную теорию, основанную на анализе движений дискретных электрических зарядов. Вывел формулу, связывающую диэлектрическую проницаемость с плотностью диэлектрика, и зависимость показателя преломления вещества от его плотности (формула Лоренца–Лоренца), дал выражение для силы, действующей на движущийся заряд в магнитном поле (сила Лоренца), объяснил зависимость электропроводности вещества от теплопроводности, развил теорию дисперсии света.
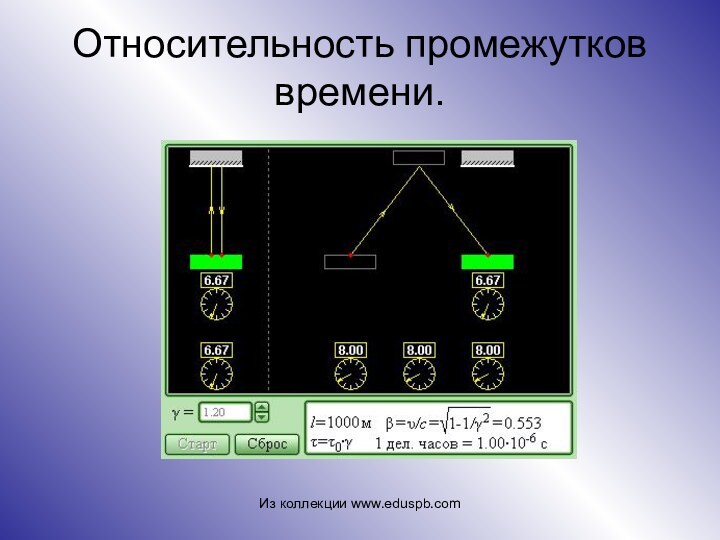
Для объяснения опыта Майкельсона–Морли выдвинул (1892) гипотезу о сокращении размеров тел в направлении их движения (сокращение Лоренца). В 1904 вывел формулы, связывающие между собой пространственные координаты и моменты времени одного и того же события в двух различных инерциальных системах отсчета (преобразования Лоренца). Подготовил переход к теории относительности.
Из коллекции www.eduspb.com