- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Синтез механизмов
Содержание
- 2. План лекции Проектирование плоских и пространственных механизмов. Синтез
- 3. Проектирование плоских и пространственных механизмов В теории механизмов
- 4. Детали, предназначенные для передачи вращательного движения, укрепляют
- 5. Передача вращательного движения между валами, оси которых
- 6. Передача вращательного движения может производиться с увеличением
- 7. Рис.1а) Передача вращательного движения между валами с параллельными осями.
- 8. Синтез трехзвенных плоских зубчатых механизмов с круглыми
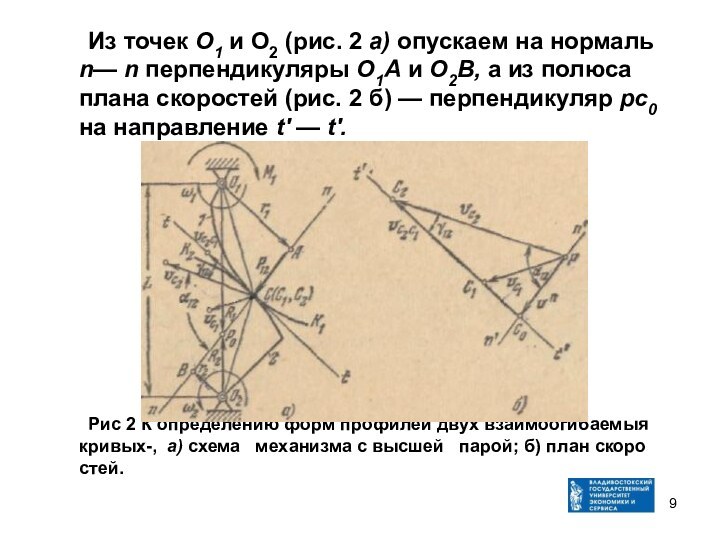
- 9. Из точек О1 и O2 (рис. 2
- 10. Отрезок (рс0) представляет собою нормальную составляющую vn
- 11. Заменяя VС1 , И VС2 их значениями,
- 12. Следовательно, передаточная функция i12 равна(2.3) Продолжим нормаль n
- 13. Эвольвенты и её свойства Эвольвента и ее свойства Эвольвента
- 14. Так как KyNy перекатывается без скольжения по
- 15. Уравнения (1) И (2) являются уравнениями эвольвенты
- 16. Рис .1
- 17. Геометрические элементы зубчатых колес Ниже даны
- 18. Геометрия эвольвентных профилей Делительной окружностью называется окружность стандартных
- 19. Модуль характеризует высоту зуба. Чем больше зуб,
- 20. Проектирование эвольвентных профилей Эвольвентную зубчатую передачу составляют, как
- 21. Линия зацепления является геометрическим местом точек контакта
- 22. Угол N1O1P = углу N2J2P = αw
- 23. Между делительными окружностями у.m – это воспринимаемое
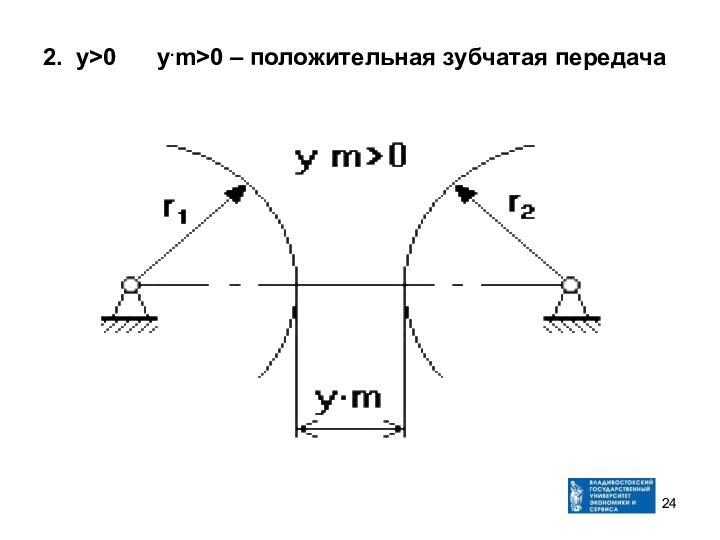
- 24. 2. у>0 у.m>0 – положительная зубчатая передача
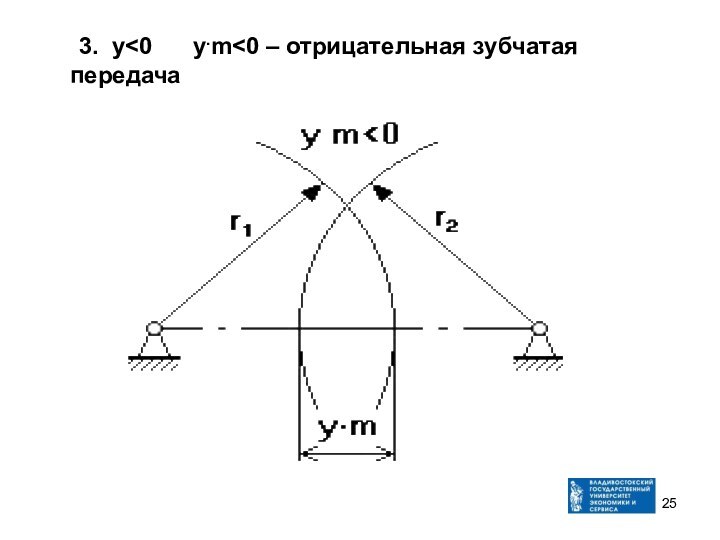
- 25. 3. у
- 26. Свойства эвольвентного зацепления. 1. Эвольвентное зацепление молочувствительно к
- 27. Винтовая передача (винт-гайка) Винтовая передача преобразует вращательное движение в поступательное. Пример винтовой передачи
- 28. Проектирование винтовой передачи ВИНТОВАЯ ПЕРЕДАЧА
- 29. Основы расчета винтовой передачи Параметры резьбы рассчитывают, исходя
- 30. В винтовых механизмах вращение винта или гайки
- 31. При малом рz1 и сравнительно большом D
- 32. Таким образом, при простой и компактной конструкции
- 33. Проектирование червячной передачи Червячная передача имеет перекрещивающиеся оси
- 34. Передаточное отношение червячной передачи находят аналогично цилиндрической
- 35. Рисунок 1 Далее расчёт проводится по формуле Герца-Беляева.
- 36. Скачать презентацию
- 37. Похожие презентации
План лекции Проектирование плоских и пространственных механизмов. Синтез трехзвенных плоских зубчатых механизмов с круглыми цилиндрическими колесами, геометрические элементы зубчатых колес, геометрия эвольвентных профилей, проектирование эвольвентных профилей. Синтез трехзвенных пространственных зубчатых механизмов, проектирование винтовой и червячной передач.































Слайд 3
Проектирование плоских и пространственных механизмов
В теории механизмов и
машин под термином синтез понимают проектирование механизмов. Для этого
сначала формулируют техническое задание, в котором должны быть отражены назначение механизма в соответствии с технологическим процессом или технологическими операциями, функции движения выходных звеньев и функции изменения сил полезных сопротивлений, а также вид источников энергии.Слайд 4 Детали, предназначенные для передачи вращательного движения, укрепляют на
валах, представляющих собой вращающиеся в опорах стержни, в большинстве
случаев цилиндрической формы. Вал, от которого передается движение, называется ведущим; вал, которому передается движение, называется ведомым.Передачу вращательного движения возможно осуществить между валами, расположенными в пространстве как угодно: оси валов могут быть параллельными, пересекаться под любым углом, а также перекрещиваться под любым углом.
Слайд 5 Передача вращательного движения между валами, оси которых параллельны,
осуществляется при помощи плоских механизмов, в остальных случаях —
при помощи пространственных механизмов.Передача вращательного движения производится одним из следующих способов:
непосредственным соприкосновением двух тел, одно из которых связано жестко с ведущим, а другое — с ведомым валом;
посредством гибких тел, сцепляющихся с телами, жестко связанными с ведущим, и ведомым валами.
Слайд 6 Передача вращательного движения может производиться с увеличением или
уменьшением угловой скорости вращения, а также без ее изменения.
Отношение
угловых скоростей вращения обоих валов называется передаточным отношением. Передаточное отношение может быть, следовательно, выражено отношением угловой скорости ведущего вала к угловой скорости ведомого вала или наоборот.Передаточное отношение в направлении силового потока, т. е. отношение угловой скорости ведущего вала к угловой скорости ведомого, называется передаточным числом*.
Слайд 8 Синтез трехзвенных плоских зубчатых механизмов с круглыми цилиндрическими
колесами
(основные сведения из теории зацепления)
Пусть передача вращения между двумя
осями 01 и 02 (рис. 2 а) с угловыми скоростями ω1 и ω2 осуществляется посредством двух взаимоогибаемых кривых К1 и К2, принадлежащих звеньям 1 и 2. Проведем в точке соприкосновения С кривых К1 и К2 нормаль n — n и касательную t — t к этим кривым.Скорости vС1 и vС2 точек С1 и С2, принадлежащих звеньям 1 и 2, связаны условием
vc1=vc1+vc2c1
План скоростей механизма, построенный по этому уравнению, показан на (рис. 2 б)
Слайд 9 Из точек О1 и O2 (рис. 2 а)
опускаем на нормаль n— n перпендикуляры О1А и О2В,
а из полюса плана скоростей (рис. 2 б) — перпендикуляр рс0 на направление t' — t'.Рис 2 К определению форм профилей двух взаимоогибаемыя кривых-, а) схема механизма с высшей парой; б) план скоростей.
Слайд 10 Отрезок (рс0) представляет собою нормальную составляющую vn векторов скоростей
vc1 и vc2
Из подобия треугольников О1АС1 и рс0с1 и
треугольников О2ВС2и рс0с2 имеем
(2.1)
Отрезки (рс1), (рc 2) и (рс0) представляют собой соответственно скорости vС1, vС2 и vn . Тогда соотношения (2.1) могут быть представлены так:
Или
Слайд 11
Заменяя VС1 , И VС2 их значениями, равными
VС1=
ω 1 (O 1 C 1) VС2= ω 2
(O 2 C 2),Получаем
vn= ω 1 (O 1 А) и vn= ω 2 (O 2 B) ,
Откуда
ω 1 (O 1 А) = ω 2 (O 2 B) . (2.2)
Слайд 12
Следовательно, передаточная функция i12 равна
(2.3)
Продолжим нормаль n —
n до пересечения в точке Р0 с отрезком (О1O2).
Тогда из подобия треугольников O1АР0 и O2ВР0 имеемИ формула (2.3) принимает окончательный вид:
(2.4)
Равенство (2.4) называется основной теоремой зацепления.
Слайд 13
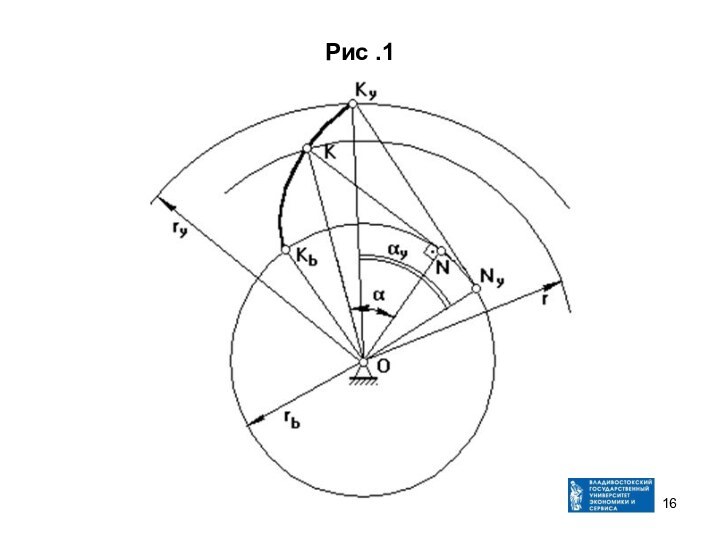
Эвольвенты и её свойства
Эвольвента и ее свойства
Эвольвента образуется
путем перекатывания производящей прямой KyNy без скольжения по основной
окружности радиуса rb (рис. 1).Радиус произвольной окружности – ry. ONy || ττ
Из треугольника ONyKy следует, что
(1)
Слайд 14 Так как KyNy перекатывается без скольжения по основной
окружности, то
(2)
rb(θy + αy) = rb.tg αy
θy =
tg αy - αy θy = inv αy
θy – инволюта;
Слайд 15 Уравнения (1) И (2) являются уравнениями эвольвенты в
параметрической форме.
αу – угол профиля эвольвенты для точки Ку,
лежащей на произвольной окружности.α – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.
Угол профиля эвольвенты для точки Кb, лежащей на основной окружности, равен нулю: αb=0.
Свойства эвольвенты:
1. Форма эвольвенты зависит от радиуса основной окружности.
2. Производящая прямая KyNy является нормалью к эвольвенте в данной тоске.
3. Эвольвента начинается от основной окружности..
Слайд 17
Геометрические элементы зубчатых колес
Ниже даны стандартные
зависимости зубчатых зацеплений, предусмотренные ГОСТ для нормального прямозубого колеса
Шаг
зацепления передачи t = πт
Высота головки зуба h' = mВысота ножки зуба h"= 1,25/72
Высота зуба h = 2,25m
Радиальный зазор е = 0,25m
Диаметр делительной окружности, выраженный в мм, de = тz
Диаметр окружности головок De — m(z -f- 2)
Диаметр окружности ножек Di=m(z— 2,5)
Слайд 18
Геометрия эвольвентных профилей
Делительной окружностью называется окружность стандартных шага
р, модуля m и угла профиля α.
Шаг – расстояние
между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:
1 ряд – наиболее предпочтительный;
2 ряд – средней предпочтительности;
3 ряд – наименее предпочтительный.
Слайд 19 Модуль характеризует высоту зуба. Чем больше зуб, тем
более шумной становится зубчатая передача.
Угол профиля – угол
между касательной к эвольвенте в данной точке и радиус-вектором данной точки.Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20о (хотя лучше 25о).
Основные расчетные зависимости:
Радиус делительной окружности
rb=r cosα; α = p cos20°
Модуль по ГОСТ
Слайд 20
Проектирование эвольвентных профилей
Эвольвентную зубчатую передачу составляют, как минимум,
из 2-х зубчатых колес, при этом в рассмотрение вводится
две начальные окружности радиусами rw1 и rw2.Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.
Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N1N2, которая одновременно касается 2-х основных окружностей rb1 и rb2.
Слайд 21 Линия зацепления является геометрическим местом точек контакта сопряженных
эвольвентных профилей.
В точке В1 пара эвольвент, которые в
данный момент времени контактируют в точке К, входят в зацепление. В точке В2 этаже пара эвольвент из зацепления выходят.На линии зацепления N1N2 все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N1N2 эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.
Слайд 22 Угол N1O1P = углу N2J2P = αw –
угол зацепления.
Для передачи, составленной из нулевых зубчатых колес
αw=20oДля передачи, составленной из положительных з. к. αw>20o
Для передачи, составленной из отрицательных з. к. αw<20o
c=c*.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.
c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).
Слайд 23
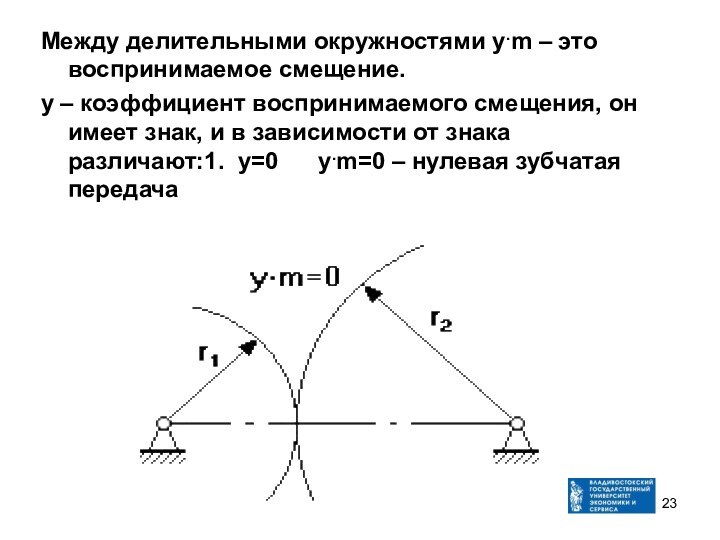
Между делительными окружностями у.m – это воспринимаемое смещение.
у
– коэффициент воспринимаемого смещения, он имеет знак, и в
зависимости от знака различают:1. у=0 у.m=0 – нулевая зубчатая передача
Слайд 26
Свойства эвольвентного зацепления.
1. Эвольвентное зацепление молочувствительно к погрешностям
изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное
отношение зубчатой передачи не изменится.2. Линия зацепления N1N2 является общей нормалью к сопряженным эвольвентным профилям.
3. Контакт эвольвент осуществляется только на линии зацепления.
Слайд 27
Винтовая передача
(винт-гайка)
Винтовая передача преобразует вращательное
движение в поступательное.
Пример винтовой передачи
Слайд 28
Проектирование винтовой передачи
ВИНТОВАЯ ПЕРЕДАЧА —
устройство, содержащее винтовую пару, у которой гайка и винт
образуют кинематические пары со стойкой или звеньями другого механизма. Причем в первом случае. Винтовая передача также называется передачей «винт—гайка».
Слайд 29
Основы расчета винтовой передачи
Параметры резьбы рассчитывают, исходя из
заданных скоростей и нагрузок на выходном звене.
Относительное перемещение гайки
и винта (ход резьбы рг) определяют в зависимости от скорости поступательного движения v и угловой скорости со винта или гайки:pz = 2πv/ω
где v — мм/с; ω — рад/с.
Слайд 30 В винтовых механизмах вращение винта или гайки осуществляется,
как правило, с помощью маховичка, шестерни и т. п.
При этом условное передаточное отношение можно выразить отношением перемещения маховичка SМ к перемещению гайки (винта)i = Sм/Sг=πD/pz,
где D —диаметр маховичка (шестерни и т. п.), pz1— ход винта.
Слайд 31 При малом рz1 и сравнительно большом D можно
получить очень большое i. Например, при рz1 = 1
мм,D = 100 мм, i = 314.
Зависимость между окружной силой Ftм на маховичке и осевой силой Fa на гайке (винте) имеет вид
Fa=Ftмiη,
где η— к. п. д. винтовой - пары.
Для i = 314 и η ≈0,3 Fa ≈ 95 Ftм
Слайд 32 Таким образом, при простой и компактной конструкции передача
винт—гайка позволяет получить большой выигрыш в силе или осуществлять
медленные и точные перемещения.-Соотношение между крутящим моментом Мк на гайке и осевой силой F a на винте имеет вид
MK = Fa d2/2 tg(γ + ρ),
где ρ — угол трения (в расчетах принимается ρ ≈ 6°, что соответствует коэффициенту трения f ≈0,1).
Слайд 33
Проектирование червячной передачи
Червячная передача имеет перекрещивающиеся оси валов,
обычно под углом 90°. Она состоит из червяка –
винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы. Движение в червячной передаче преобразуется по принципу винтовой пары. Изобретателем червячных передач считают Архимеда.
Слайд 34
Передаточное отношение червячной передачи находят аналогично цилиндрической
U
= n1 / n2 = Z2 / Z1.
Здесь Z2
– число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.В осевом сечении червячная пара (рис .1) фактически представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности "рейки" (винта червяка) ρ1 равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса ρпр = ρ2.
Слайд 35
Рисунок 1
Далее расчёт проводится по формуле Герца-Беляева. Из
проектировочного расчёта находят осевой модуль червяка, а по нему
и все геометрические параметры зацепления.Особенность расчёта на изгиб состоит в том, что принимается эквивалентное число зубьев Zэкв = Z2 / cos3γ, где γ - угол подъёма витков червяка.





























