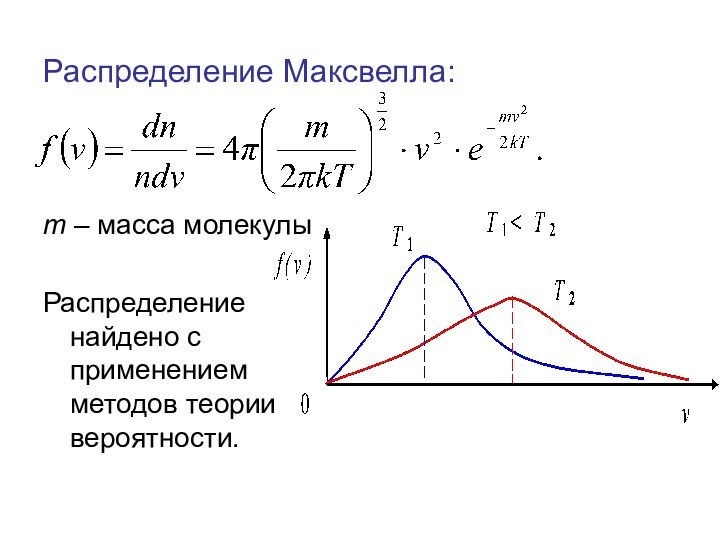
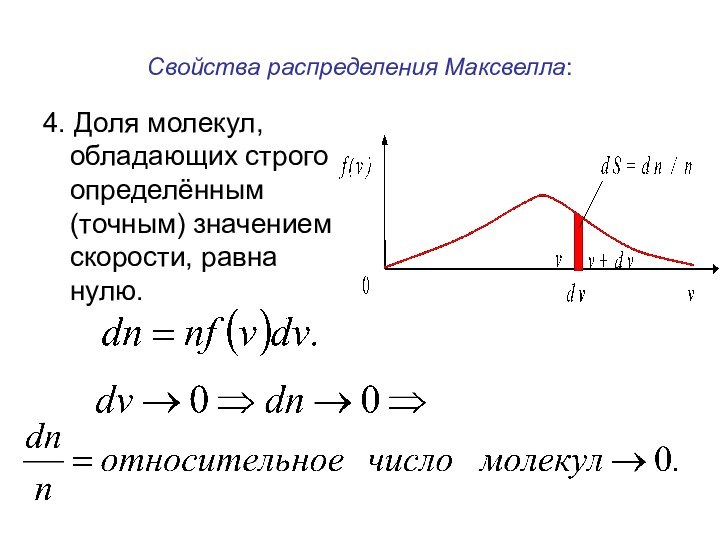
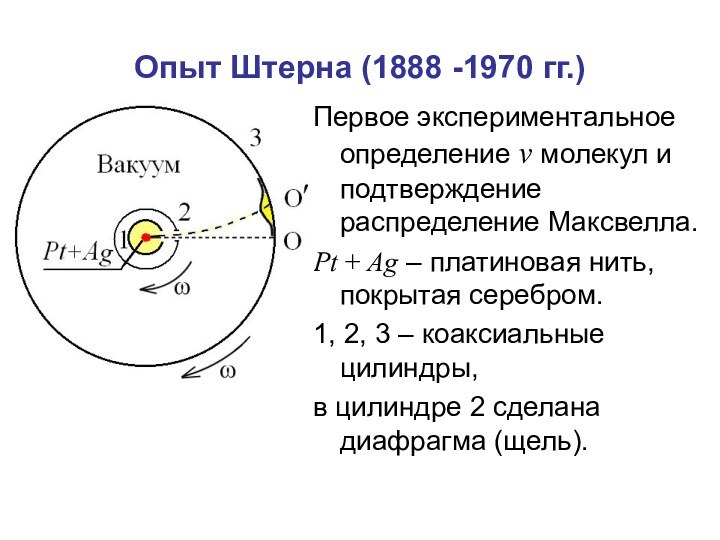
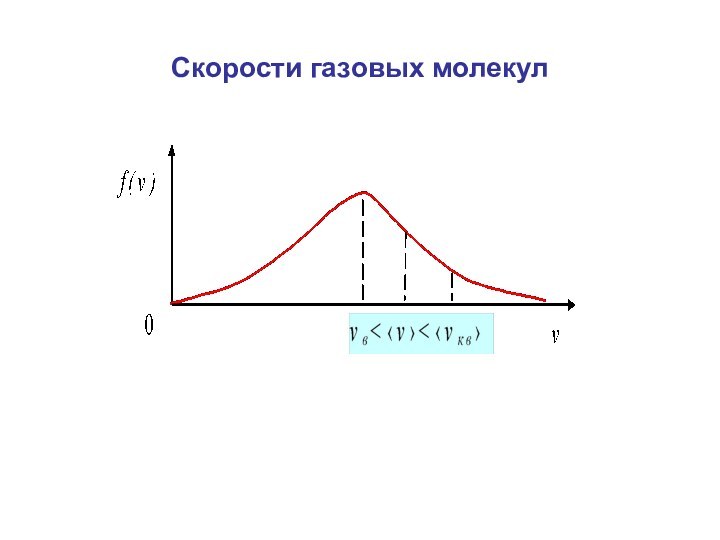
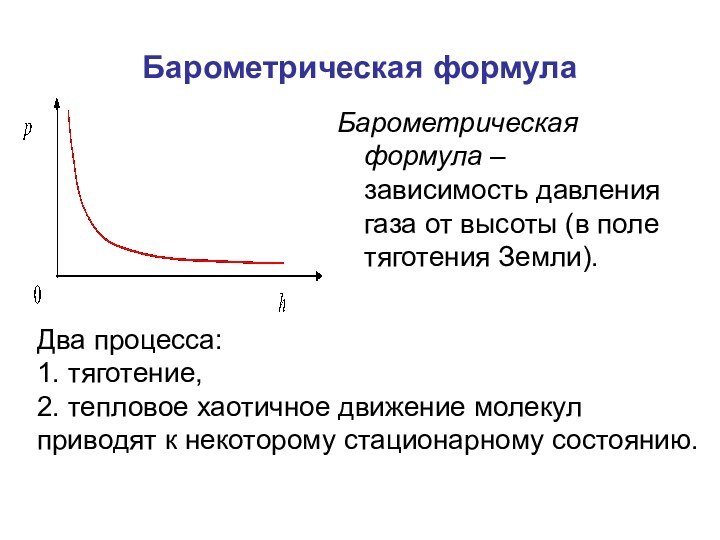
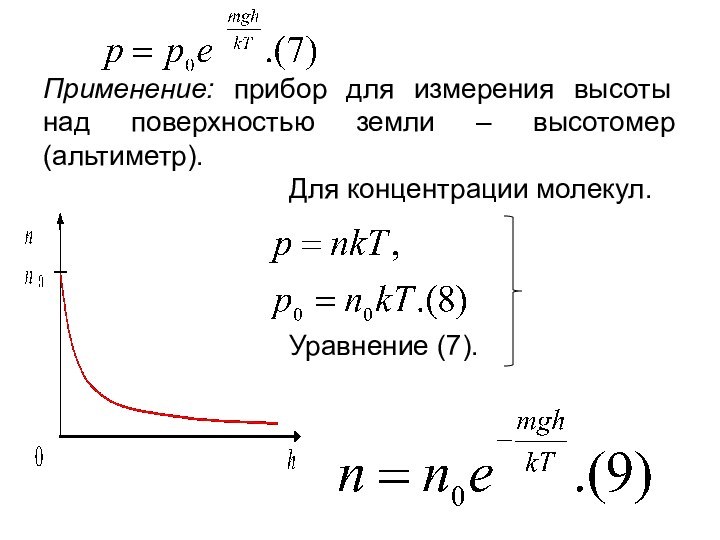
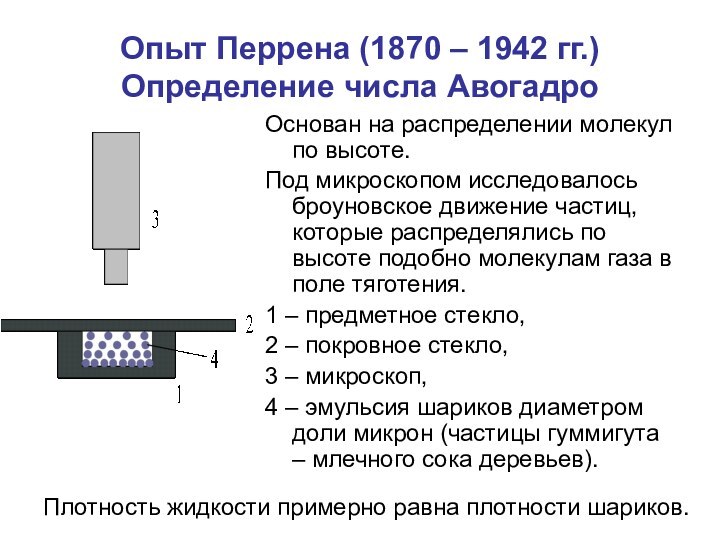
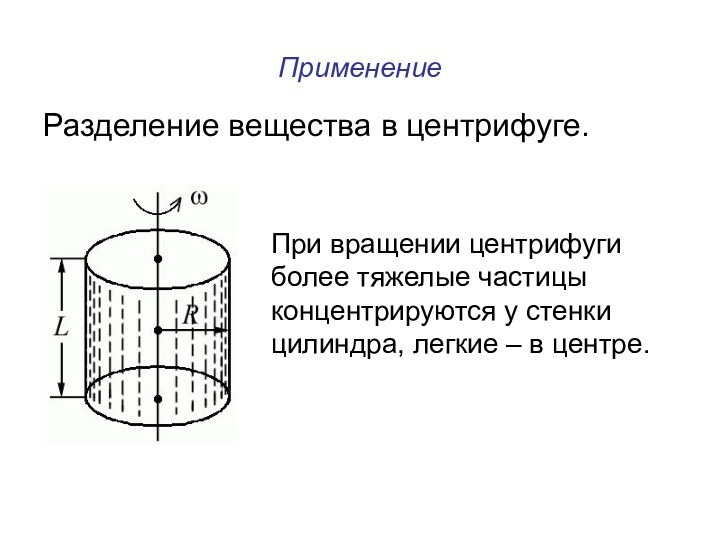
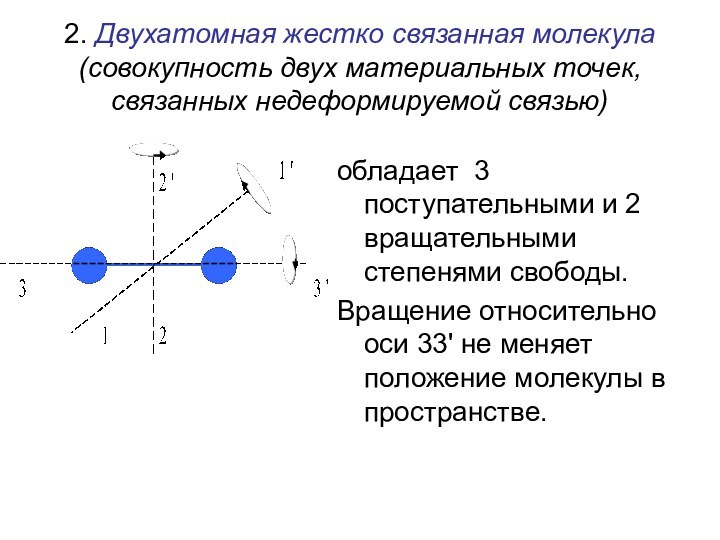
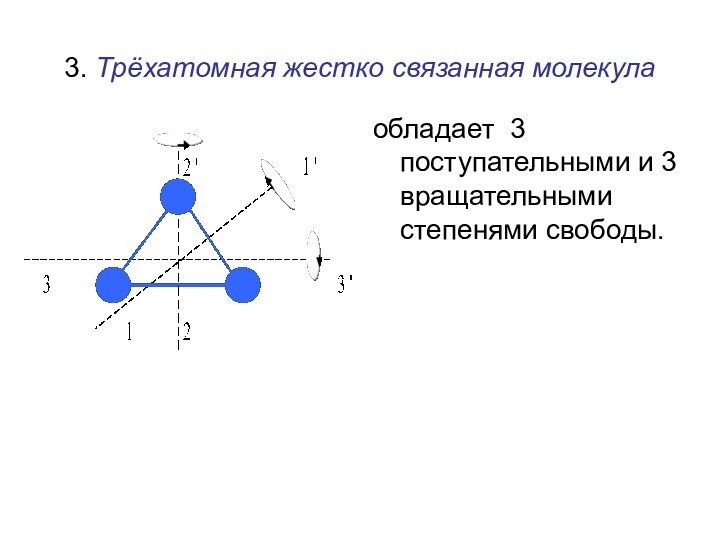
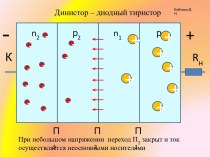
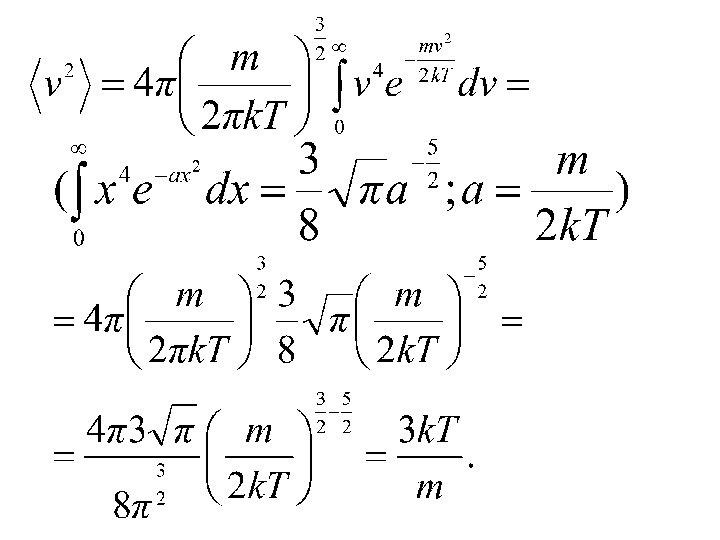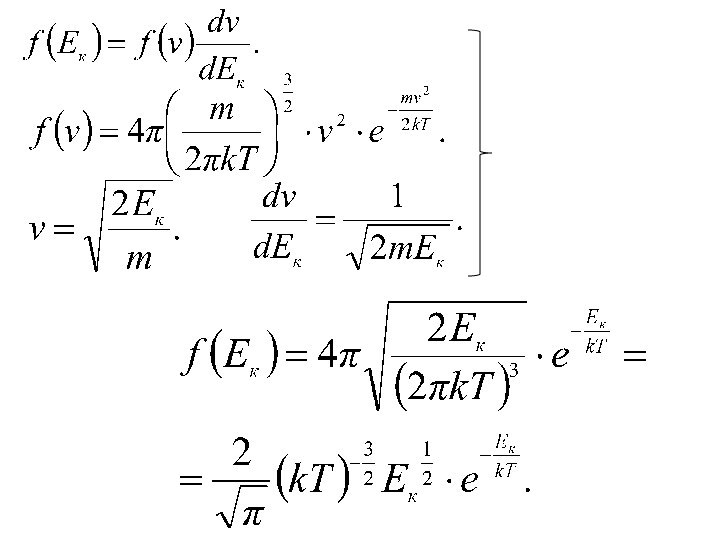времени.
Рассмотрим систему, состоящую из n тел, движущихся со скоростями
v1, v2 … vn.Скорость средняя по ансамблю:
где v1, v2 … vn измерены в
один момент времени.
Скорость средняя по времени:
где v1, v2 … vn измерены для
одной молекулы в разные моменты времени.