Слайд 2
Тема 5 УПРУГИЕ ВОЛНЫ
5.1 Распространение волн в
упругой среде
Сегодня:
5.2 Уравнение плоской и сферической волны
5.3
Фазовая скорость
5.4 Принцип суперпозиции. Групповая скорость
5.5 Стоячие волны
5.6 Волновое уравнение
5.7 Эффект Доплера
Слайд 3
5.1 Распространение волн в упругой среде
Колеблющиеся тело, помещенное
в упругую среду, является источником колебаний, распространяющихся от него
во все стороны.
Круговая волна на поверхности жидкости, возбуждаемая точечным источником
Генерация акустической волны громкоговорителем.
Процесс распространения колебаний в пространстве называется волной
Слайд 4
При распространении волны, частицы среды не движутся вместе
с волной, а колеблются около своих положений равновесия.
Вместе
с волной от частицы к частице, передается лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн независимо от их природы является перенос энергии без переноса вещества.
Слайд 5
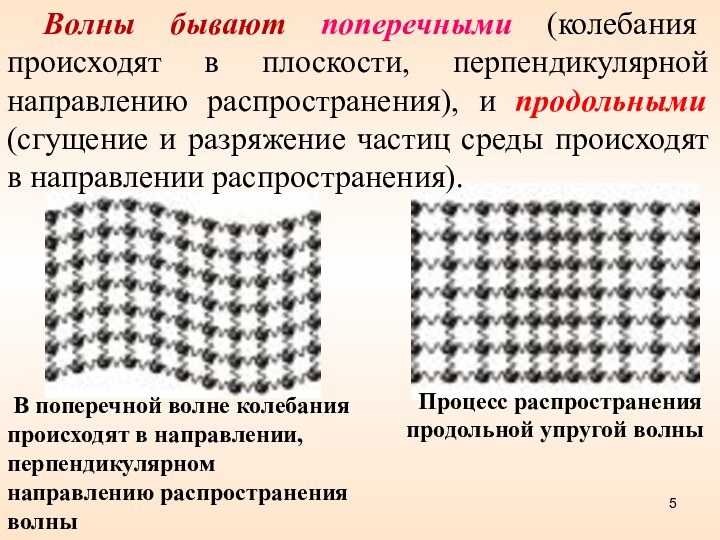
Волны бывают поперечными (колебания происходят в плоскости, перпендикулярной
направлению распространения), и продольными (сгущение и разряжение частиц среды
происходят в направлении распространения).
Процесс распространения
продольной упругой волны
В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны
Слайд 6
Если взаимосвязь между частицами среды осуществляется силами
упругости, возникающими вследствие деформации среды при передаче колебаний от
одних частиц к другим, то волны называются упругими (звуковые, ультразвуковые, сейсмические и др. волны).
Упругие поперечные волны возникают в среде, обладающей сопротивлением сдвигу,
вследствие этого:
в жидкой и газообразной средах возможно возникновение только продольных волн;
в твердой среде возможно возникновение как продольных, так и поперечных волн.
Слайд 7
Наложение продольной и поперечной волн равной амплитуды, сдвинутых
по фазе на π/2.
В результате каждая масса совершает
круговые движения.
Слайд 8
Волна на поверхности жидкости - суперпозиция продольного и
поперечного движения молекул
Слайд 9
Движение молекул в волне на поверхности
жидкости
У поверхностных волн взаимосвязь между соседними молекулами при передаче колебаний осуществляется не силами упругости, а силами поверхностного натяжения и тяжести. В случае малой амплитуды волны каждая молекула движется по окружности, радиус которой убывает с расстоянием от поверхности. Нижние молекулы находятся в покое
Слайд 10
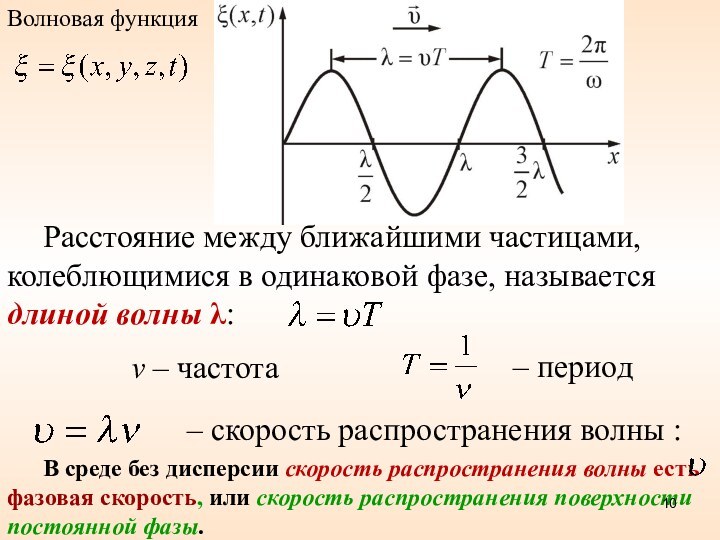
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе,
называется длиной волны :
– скорость распространения волны :
–
период
– частота
В среде без дисперсии скорость распространения волны есть фазовая скорость, или скорость распространения поверхности постоянной фазы.
Волновая функция
Слайд 11
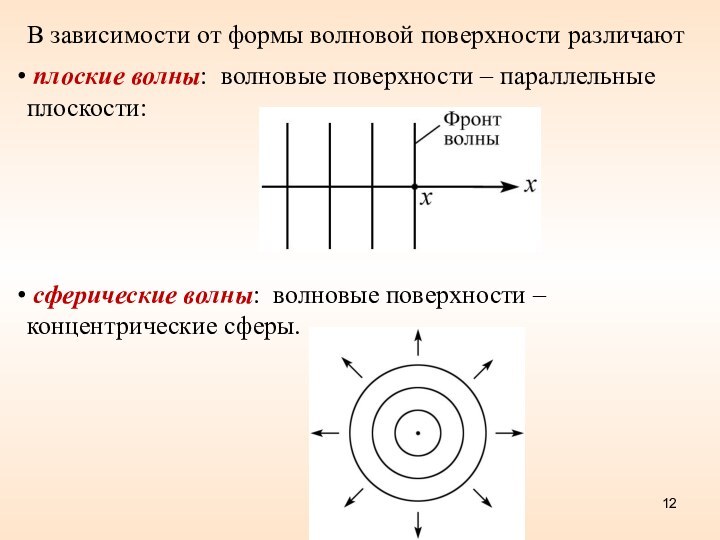
Волновая поверхность – геометрическое место точек, колеблющихся в
одинаковой фазе.
Число волновых поверхностей – бесконечно.
Фронт волны – один.
Волновые поверхности неподвижны,
Фронт волны все время перемещается
Слайд 13
5.2 Уравнение плоской и сферической волны
Уравнением волны
– называется выражение, которое дает смещение колеблющейся точки как
функцию ее координат (x, y, z) и времени t.
Слайд 14
Уравнение плоской волны
Найдем вид волновой функции,
в случае плоской волны предполагая, что колебания носят гармонический
характер:
Чтобы пройти путь x необходимо время
– это уравнение плоской волны.
Пусть
Слайд 15
Введем волновое число
или в векторной форме
Так
как
, то
Отсюда
Тогда уравнение плоской
волны запишется
так:
Слайд 16
При поглощении средой энергии волны:
-наблюдается
затухание волны (уменьшение интенсивности волны по мере удаления от
источника колебаний);
β – коэффициент затухания;
А – амплитуда.
Слайд 17
Уравнение сферической волны
Амплитуда колебаний
убывает по закону
Уравнение сферической волны:
или
Пусть
При поглощении средой энергии волны:
β
– коэффициент затухания.
Слайд 18
5.6 Волновое уравнение
Распространение
волн в однородной среде в общем случае описывается волновым
уравнением – дифференциальным уравнением в частных производных:
или
Всякая функция, удовлетворяющая этому уравнению, описывает некоторую волну, причем -фазовая скорость волны
Слайд 19
Решением волнового уравнения
является уравнение любой
волны, например
сферической:
или плоской :
Для плоской волны, распространяющейся вдоль
оси x, волновое уравнение упрощается:
Напоминаю, что =
оператор Лапласа:
Слайд 20
5.3 Фазовая скорость
– это скорость распространения фазы
волны.
– скорость распространения фазы есть
скорость распространения
волны.
Для синусоидальной волны скорость переноса
энергии равна фазовой скорости.
Слайд 21
5.4 Принцип суперпозиции. Групповая скорость
Принцип суперпозиции (наложения
волн): при распространении в среде нескольких волн каждая из
них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений частиц.
Исходя из этого принципа и разложения Фурье, любая волна может быть представлена в виде волнового пакета или группы волн.
Слайд 22
Строго монохроматическая волна представляет собой бесконечную во времени
и пространстве последовательность «горбов» и «впадин».
Фазовая скорость этой
волны
или
Слайд 23
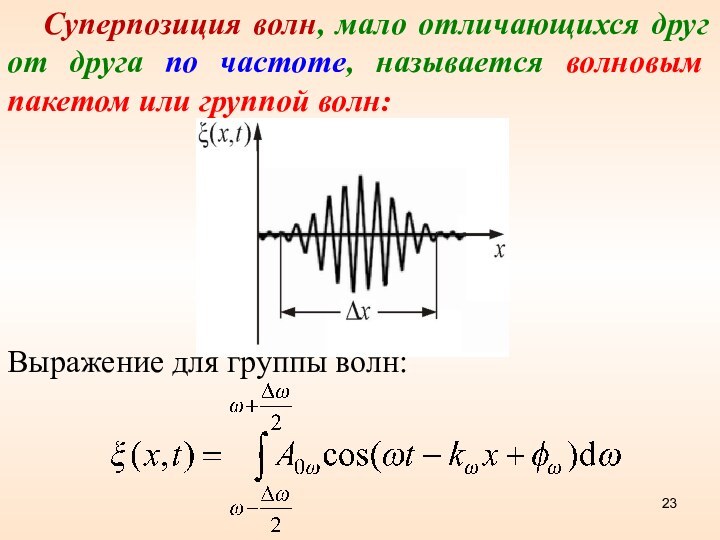
Суперпозиция волн, мало отличающихся друг от друга по
частоте, называется волновым пакетом или группой волн:
Выражение для
группы волн:
Слайд 24
Там где фазы совпадают, наблюдается усиление амплитуды,
где нет – гашение (результат интерференции).
необходимо условие
Слайд 25
Дисперсия – это зависимость фазовой скорости в
среде от частоты.
В недиспергирующей среде все плоские волны,
образующие пакет, распространяются с одинаковой фазовой скоростью υ.
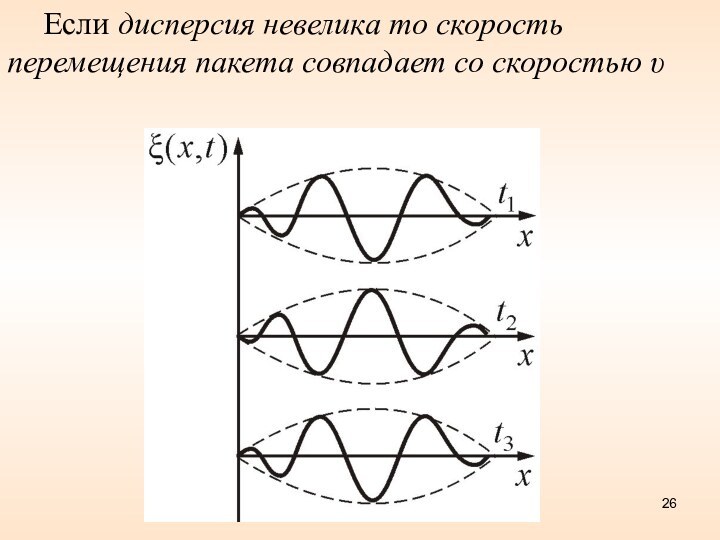
Скорость перемещения пакета u совпадает со скоростью υ:
Скорость, с которой перемещается центр пакета (точка с максимальным значением А), называется групповой скоростью u.
В диспергирующей среде
Слайд 26
Если дисперсия невелика то скорость перемещения пакета совпадает
со скоростью υ
Слайд 27
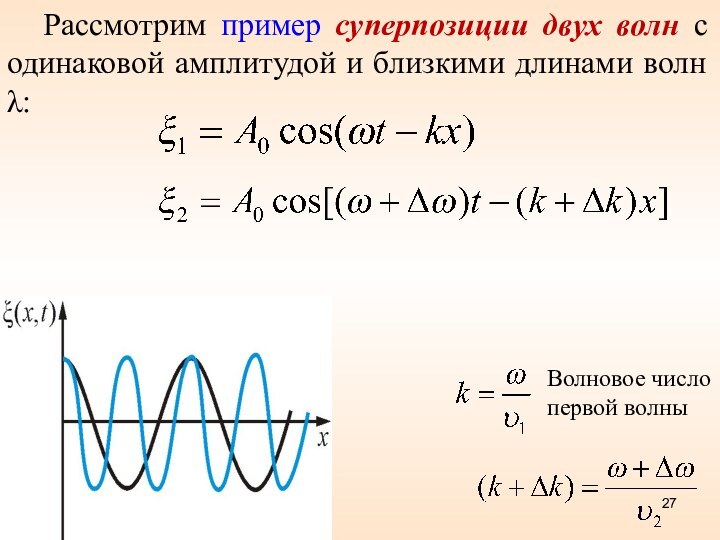
Рассмотрим пример суперпозиции двух волн с одинаковой амплитудой
и близкими длинами волн :
Волновое число
первой волны
Слайд 28
В результате суперпозиции двух волн получилась
суммарная волна (волновой пакет):
Эта волна отличается
от гармонической тем, что её амплитуда – есть медленно изменяющаяся функция х и t :
Максимум амплитуды :
- координаты максимума
Слайд 29
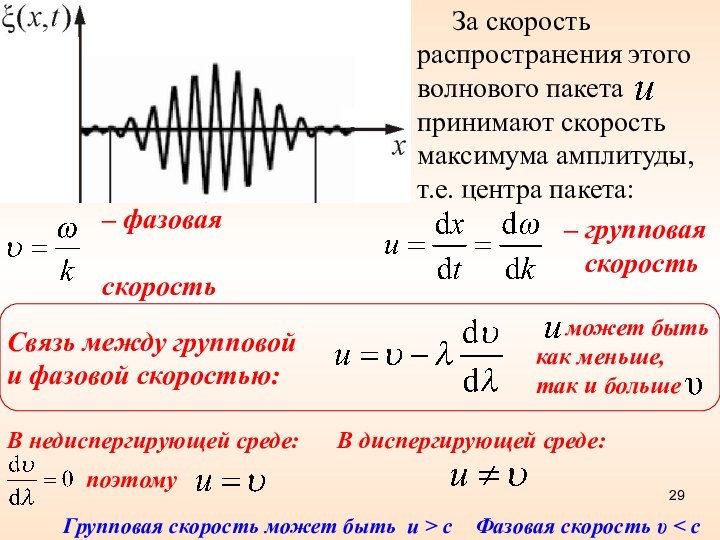
– фазовая
скорость
За скорость
распространения этого волнового пакета принимают скорость максимума амплитуды, т.е.
центра пакета:
– групповая
скорость
Связь между групповой и фазовой скоростью:
может быть как меньше, так и больше
В недиспергирующей среде: В диспергирующей среде:
Групповая скорость может быть u > c Фазовая скорость υ < c
поэтому
Слайд 30
5.5 Стоячие волны
Если в среде распространяется несколько
волн, то колебания частиц среды оказывается геометрической суммой колебаний,
которые совершали бы частицы при распространении каждой из волн в отдельности.
Волны накладываются друг на друга не возмущая (не искажая друг друга) - принцип суперпозиции волн.
Если две волны, приходящие в какую либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными.
При сложении когерентных волн возникает явление интерференции.
Слайд 31
Очень важный случай интерференции наблюдается при наложении двух
встречных плоских волн с одинаковой амплитудой.
Возникающий в результате
колебательный процесс называется стоячей волной.
Практически стоячие волны возникают при отражении от преград.
или
уравнение стоячей
волны – частный случай
интерференции
Слайд 32
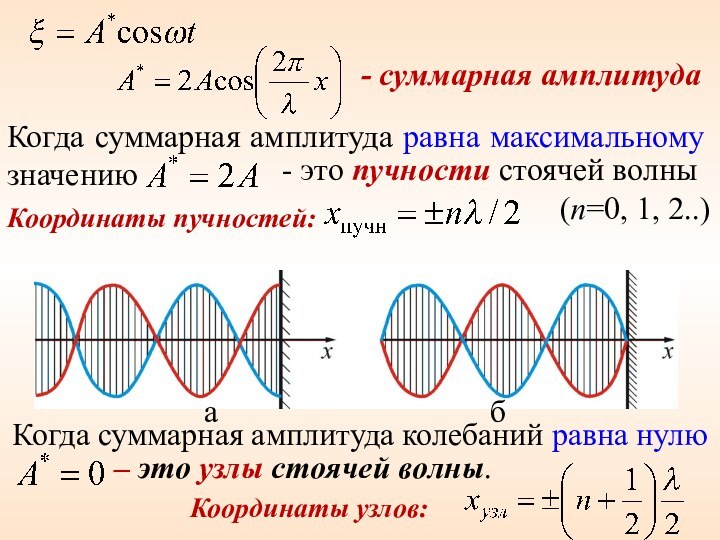
- суммарная амплитуда
Когда суммарная амплитуда равна
максимальному значению
- это пучности стоячей волны
Координаты пучностей:
а
б
Когда суммарная амплитуда колебаний равна нулю
– это узлы стоячей волны.
Координаты узлов:
(n=0, 1, 2..)
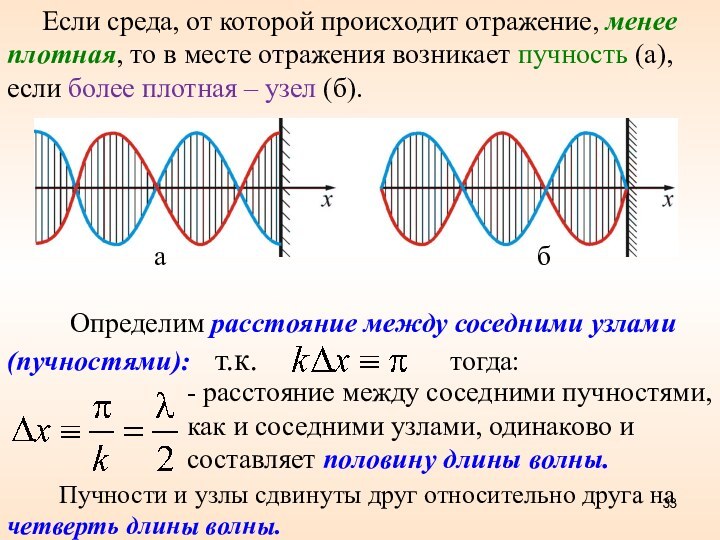
Слайд 33
- расстояние между соседними пучностями, как и соседними
узлами, одинаково и составляет половину длины волны.
Слайд 34
Если рассматривать бегущую волну, то в направлении ее
распространения переносится энергия колебательного движения.
В случае же стоячей
волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
Слайд 36
Процесс распространения продольной упругой волны
Слайд 37
ρ – плотность среды.
G –
модуль сдвига.
- плотность энергии упругой волны (как поперечной, так
и продольной) в каждый момент времени в разных точках пространства различна.
Слайд 38
Эффект Доплера
Зависимость длины волны
от относительной скорости
движения
Слайд 39
5.7 Эффект Доплера
Доплер Христиан (1803 – 1853), австрийский
физик и астроном,
член Венской АН (1848 г.).
Учился в Зальцбурге и Вене. С 1847 г. профессор Горной академии в Хемнице, с 1850 г.
профессор Политехнического института и уни-верситета в Вене. Основные труды посвящены аберрации света, теории микроскопа и оптического дальномера, теории цветов и др. В 1842 г. теоретически обосновал зависимость частоты колебаний, воспринимаемых наблюдателем, от скорости и направления движения наблюдателя относительно источника колебаний.
Слайд 41
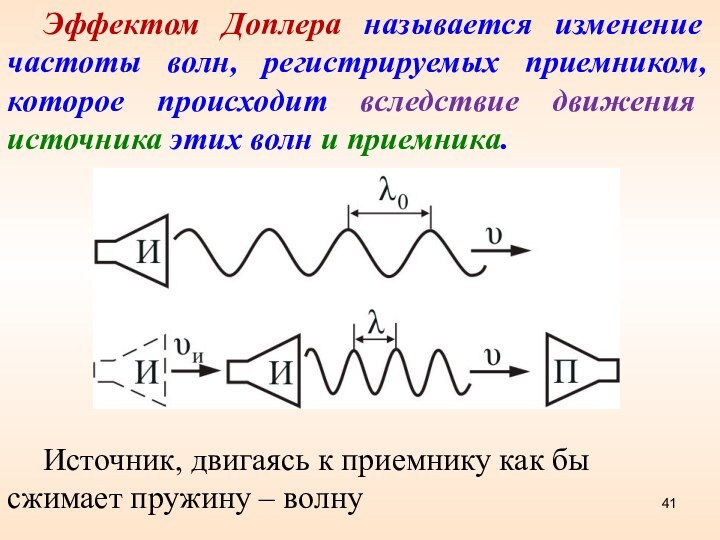
Эффектом Доплера называется изменение частоты волн, регистрируемых приемником,
которое происходит вследствие движения источника этих волн и приемника.
Источник,
двигаясь к приемнику как бы сжимает пружину – волну
Слайд 42
Волновые фронты
неподвижного источника
Слайд 45
Скорость движущегося источника
равна фазовой скорости
Слайд 46
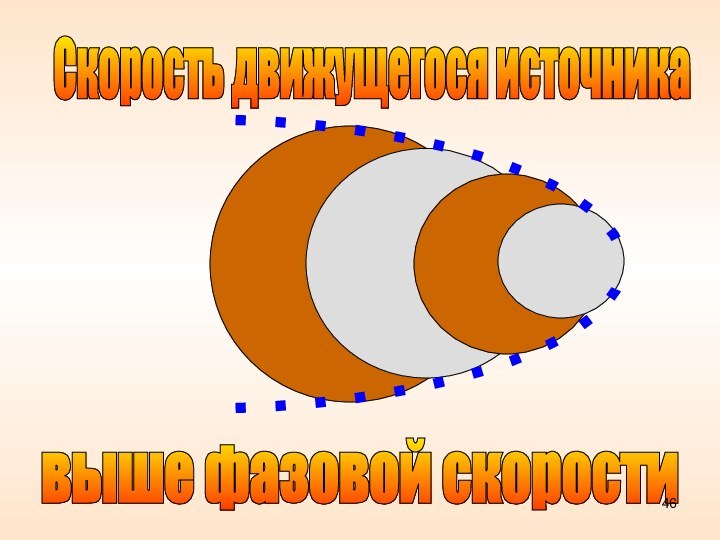
Скорость движущегося источника
выше фазовой скорости
Слайд 49
Акустический эффект Доплера
(несколько случаев проявления)
1. Источник движется
относительно приемника
Источник смещается в среде за время, равное
периоду его колебаний T0, на расстояние
где ν0 – частота колебаний источника,
υ – фазовая скорость волны
Слайд 50
Частота волны,
регистрируемая приемником,
Если вектор
скорости
источника направлен под
произвольным углом θ1 к радиус-вектору
Длина волны,
регистрируемая приемником,
Слайд 51
2. Приемник движется относительно источника
Частота волны,
регистрируемая приемником:
Если приемник движется относительно источника под углом:
Слайд 52
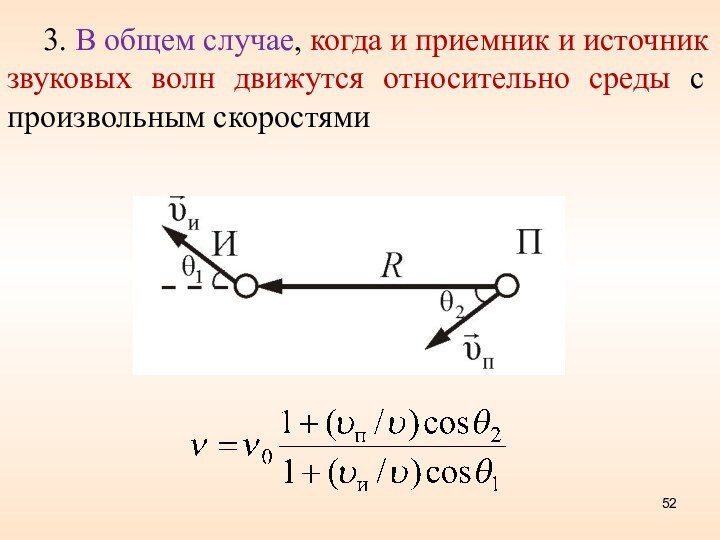
3. В общем случае, когда и приемник и
источник звуковых волн движутся относительно среды с произвольным скоростями
Слайд 53
где
– скорость источника волны относительно приемника, а
θ – угол между векторами
и
Величина
, равная проекции
на направление , называется лучевой скоростью источника.
Если
Слайд 54
Оптический эффект Доплера
Соотношение, описывающее эффект Доплера для
электромагнитных волн в вакууме, с учетом преобразований Лоренца, имеет
вид:
Если источник движется относительно приемника вдоль соединяющей их прямой, то наблюдается продольный эффект Доплера:
(1)
Слайд 55
В случае сближения источника и приемника (θ
= π)
В случае их взаимного удаления (θ
= 0)
(2)
Продольный эффект Доплера
Слайд 56
, следовательно, он значительно слабее
Поперечный эффект
пропорционален отношению
продольного, который пропорционален
Впервые экспериментальная проверка существования
эффекта Доплера и правильности релятивистской формулы (1) была осуществлена американскими физиками Г. Айвсом и Д. Стилуэллом в 30-ых гг.
Поперечный эффект Доплера
наблюдается при
Слайд 57
Эффект Доплера нашел широкое применение в науке и
технике. Особенно большую роль это явление играет в астрофизике.
На основании доплеровского смещения линий поглощения в спектрах звезд и туманностей можно определять лучевые скорости
этих объектов по
отношению к Земле: при
по формуле (1)
Слайд 58
Американский астроном Э. Хаббл обнаружил в 1929 г.
явление, получившее название космологического красного смещения и состоящее в
том, что линии в спектрах излучения внегалактических объектов смещены в сторону меньших частот (больших длин волн).
Слайд 59
Красное космологическое смещение
линий спектра водорода
65млн. св. лет
325млн. св.
лет
4 млрд. св. лет
Дева
Персей
СL 0939
Слайд 60
Космологическое красное смещение есть не что иное, как
эффект Доплера. Оно свидетельствует о том, что Метагалактика расширяется,
так что внегалактические объекты удаляются от нашей Галактики.
Под метагалактикой понимают совокупность всех звездных систем. В современные телескопы можно наблюдать часть Метагалактики, оптический радиус которой равен
Слайд 61
Хаббл установил закон, согласно которому, относительное красное смещение
растет пропорционально расстоянию r до них.
Закон Хаббла:
галактик
– постоянная
Хаббла.
которое свет проходит в вакууме за 3,27 лет
1 пк (парсек) – расстояние,
Слайд 63
На эффекте Доплера основаны радиолокационные, лазерные методы измерения
скоростей различных объектов на Земле (например, автомобиля, самолета и
др.).