Презентация на тему Теорема Гаусса

разбить эту поверхность на малые площадки ΔSi, определить элементарные

через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора

через замкнутую поверхность S

В случае замкнутой поверхности всегда выбирается внешняя нормаль.

произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри

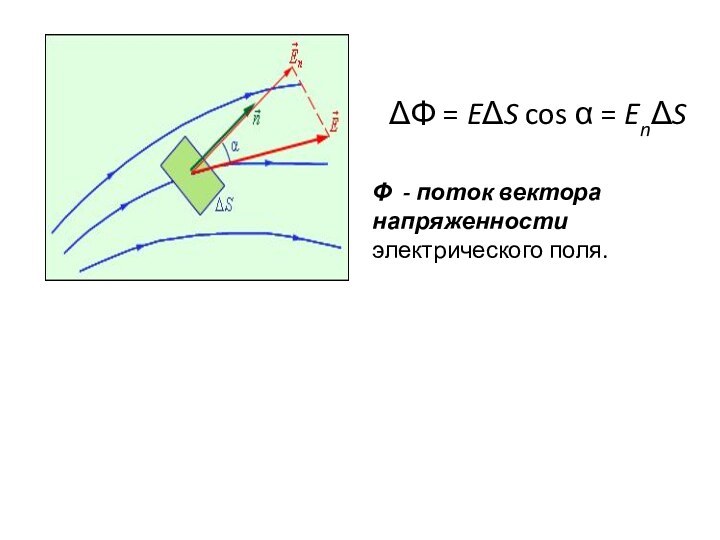
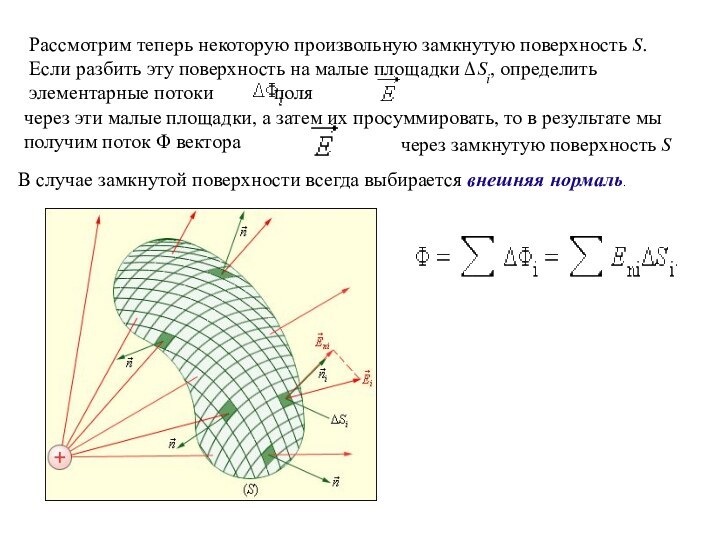
вычислить напряженность электрического поля вокруг заряженного тела, если заданное

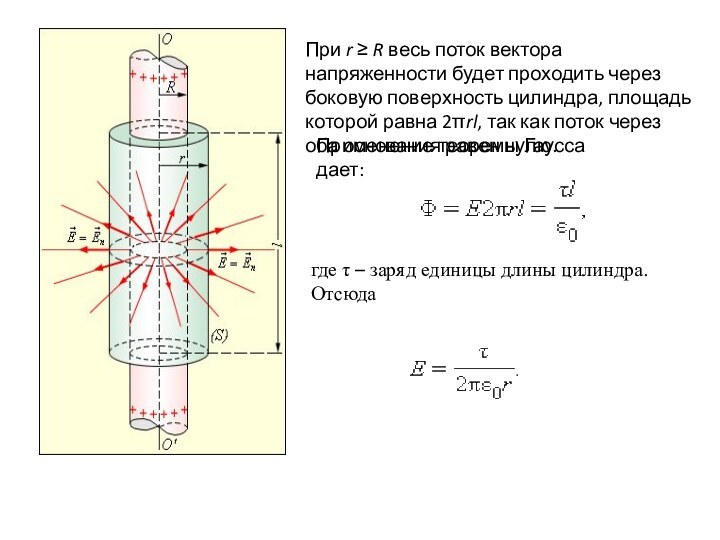
задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R.
Эта задача имеет осевую симметрию. Из соображений симметрии, электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов

через боковую поверхность цилиндра, площадь которой равна 2πrl, так

Применение теоремы Гаусса дает:

где τ – заряд единицы длины цилиндра. Отсюда