Слайд 2
1.Важнейшее свойство живых систем заключается в их способности
улавливать, преобразовывать и запасать энергию в различных формах.
Общие законы
превращения энергии изучаются термодинамикой (Т).
2. Законы термодинамики универсальны для живой и неживой природы, но Т изучает закономерности, не связанные с конкретной атомно-молекулярной структурой вещества. Т – феноменологическая наука.
Законы и методы термодинамики приложимы только к макроскопическим системам, состоящим из большого числа частиц.
Согласно I закону Т, различные виды энергии могут переходить друг в друга, но при этих превращениях энергия не исчезает и не появляется из ничего. Это закон сохранения энергии.
Слайд 3
Формулировка 1-го закона термодинамики для различных
термодинамических систем
В изолированной
системе полный запас энергии – величина постоянная и возможны
только превращения одного вида энергии в другой:
U = const ∆U = 0
В замкнутой системе изменение внутренней энергии ∆U равно сумме подведенного к системе тепла ∆Q и произведенной над данной системой работы ∆А:
∆U = ∆Q + ∆А
В открытой системе все виды работ в организме совершаются за счет эквивалентного количества энергии, выделяемой при окислении питательных веществ.
∆U = ∆Q + ∆А
1-й закон термодинамики подводит энергетический баланс организма и запрещает существование вечного двигателя 1-го рода, который мог бы производить больше энергии, чем потреблял бы в процессе своей работы (т.е. мог бы «создавать энергию»).
Слайд 4
Антуан Лоран Лавуазье
(1743-1794)
Пьер-Симон де Лаплас
(1749-1827)
Анри Лавуазье и Пьер
Лаплас показали, что дыхание животных есть медленное горение, за
счёт которого в организме поддерживается всегда постоянный запас тепла. Исследования «химии» животной теплоты, проведенные Лавуазье и Лапласом, стали первым важным шагом в борьбе с витализмом — учением, которое господствовало в биологии так же, как учение о флогистоне — в химии, и согласно которому всеми жизненными процессами управляла особая нематериальная «жизненная сила».
Применимость I закона термодинамики к живым системам
Пневматическая установка
Ледяной калориметр
Слайд 5
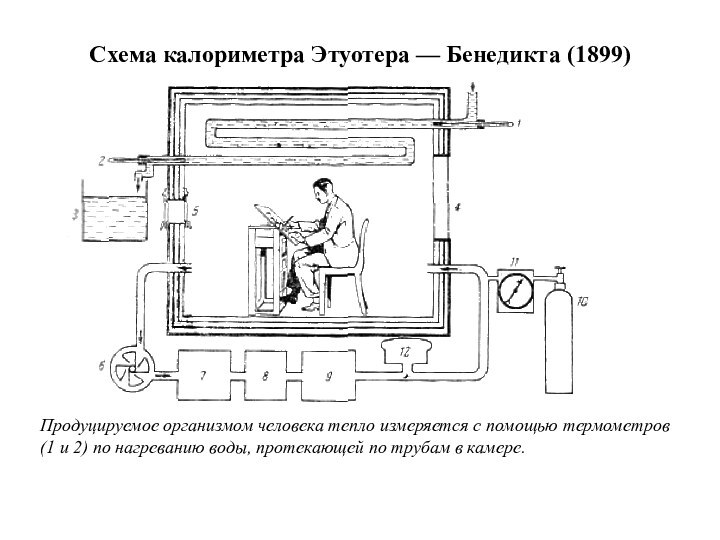
Схема калориметра Этуотера — Бенедикта (1899)
Продуцируемое организмом человека
тепло измеряется с помощью термометров (1 и 2) по
нагреванию воды, протекающей по трубам в камере.
Слайд 6
Живые организмы - открытые термодинамические системы, существующие в
условиях постоянного давления и температуры. Поэтому для оценки их
жизнедеятельности важна еще одна термодинамическая функция - энтальпия.
Энтальпия (от греч. - нагреваю) - это та энергия, которая доступна для преобразования в теплоту при определен-ных температуре и давлении.
Рассчитывается по формуле:
H=U + P∙V
где Н - энтальпия, U - внутренняя энергия, P - давление, V - объём.
Слайд 7
Второе начало термодинамики имеет несколько формулировок, но в
главном – это фундаментальный закон монотонного возрастания энтропии. Первый
закон всех наук (А.Эйнштейн), высший метафизический
закон Вселенной (А.Эддингтон).
Слайд 8
1850 г. - Немецкий физик Рудольф Клаузиус
сформулировал второе начало термодинамики.
«Теплота не может сама собою перейти
от более холодного тела к более тёплому».
В 1865г. ввёл понятие энтропии
«Энергия мира не изменяется. Энтропия мира стремится к максимуму.»
(от греч. Entropía - превращение)
Слайд 9
Невозможен вечный двигатель 2-го рода, т.е. невозможна машина,
которая изотермически превращала бы тепло в работу (У.Томсон)
Уильям Томсон
(лорд Кельвин)
Слайд 10
Первый закон утверждает
нас в мысли, что «нечто», называемое нами энергией, постоянно,
второй же закон говорит о все возрастающей недоступности этой энергии из-за другого «нечто», называемого нами энтропией (Уильямс).
Увеличение энтропии (S) является платой, взимаемой природой за каждое использование энергии (А.Г.Пасынский).
2-ой закон термодинамики – «стрела времени» самопроизвольной эволюции системы (А.Эддингтон)
Слайд 11
Под энтропией (S )
понимают количество теплоты, которое уже не может быть превращено
в механическую работу. Это некоторое количество энергии, которая остается недоступной для дальнейшего использования.
Согласно Р. Клаузиусу, энергия Вселенной постоянна (если она и теряется, то теряется не количественно, а качественно), энтропия же стремится к максимуму. И производство энтропии определяет направление течения процесса.
Слайд 12
1.Энтропия – это физическая величина, характеризующая значение связанной
энергии данной системы, приходящейся на единицу температуры (1К) .
2.Изменение
энтропии ΔS системы равно отношению количества теплоты (ΔQ), сообщенного системе, к температуре (Т):
ΔS = ΔQ/T
3.Энтропия является функцией состояния, т. е. определяется параметрами системы в данный момент и совершенно не зависит от её «истории».
4.Энтропия - это мера неупорядоченности состояния системы. Энтропия измеряется в тех же единицах, что и теплоемкость, - Дж/моль∙К, где К - температура по Кельвину.
5.Энтропия изолированной системы сохраняет постоянные значения для обратимых процессов (S=const), возрастает при необратимых (S>0) и достигает максимума при термодинамическом равновесии.
ΔS = ΔQ/T ≥ 0
dS ≥ 0
Слайд 13
1.На основе атомистической гипотезы
и кинетической теории газов Больцман впервые дал физическую трактовку
энтропии, исходя из понятий статистической физики.
2. По Больцману, энтропия – мера молекулярного хаоса и закон ее возрастания отражает возрастающую дезорганизацию системы.
3. Энтропия каждого макросостояния связана с вероятностью реализации этого состояния, т.е. с термодинамической вероятностью (W):
S=k ln W
S - энтропия
W – термодинамическая вероятность
k - константа Больцмана : k= R/ NА
Людвиг Больцман (1844-1906)
NA - число Авогадро (NА= 6,02•1023 моль-1)
R - универсальная газовая постоянная
(R= 8,3 Дж/моль*К)
Слайд 14
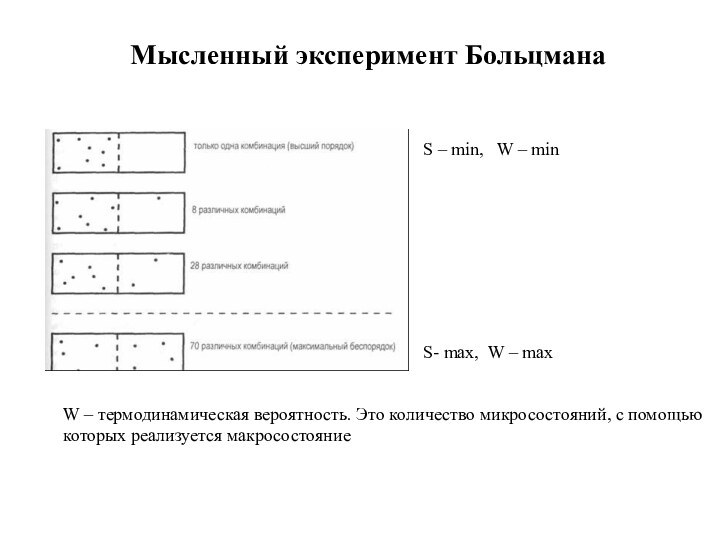
Мысленный эксперимент Больцмана
S- max, W – max
S –
min, W – min
W – термодинамическая вероятность.
Это количество микросостояний, с помощью
которых реализуется макросостояние
Слайд 15
Энтропия (S) в статистической
физике определяется как логарифмическая функция вероятности равновесного состояния системы
частиц (для которых известны вероятности распределения по энергиям).
Переходя к биологии, Больцман указывает: «Всеобщая борьба за существование живых существ не является борьбой за составные элементы, но это борьба за энтропию, которую можно использовать при переходе энергии от горячего Солнца к холодной Земле».
Слайд 16
Памятник Больцману на центральном кладбище Вены; на нем
выгравировано соотношение Больцмана
S =
k⋅logW.
(Работа Дитера Фламма)
Слайд 17
Живые организмы – открытые системы, и изменение энтропии
для них складывается из:
1)продукции энтропии внутри организма за
счет необратимых биохимических процессов
2)обмена энтропией с окружающей средой.
Формулировка второго закона термодинамики для живых организмов:
скорость изменения энтропии в организме равна алгебраической сумме производства энтропии внутри организма и скорости поступления энтропии из среды (негэнтропии) в организм: S = Si + (-Se)
Слайд 18
Свободная и связанная энергия. Обратимые и необратимые процессы.
Часть
внутренней энергии системы, которую можно использовать для совершения работы,
называется свободной энергией (G)
Остальную часть внутренней энергии системы, которую нельзя превратить в работу, называют связанной энергией (Wсв)
U = G + Wсв
Работа, совершаемая системой в любом процессе, не может быть больше, чем изменение свободной энергии: А < G
Обратимый процесс – такой процесс, при
котором при затрате работы А = δG
можно полностью вернуть систему (из
состояния B) в исходное состояние (А)
А
B
G1
G2 + Wсв
δG
Необратимый процесс – такой процесс, при
котором при затрате работы невозможно полностью вернуть систему (из состояния B) в исходное состояние (А), вследствие преобразования части свободной энергии (G) в связанную.
Это явление носит название диссипации (рассеяние) свободной энергии.
Слайд 19
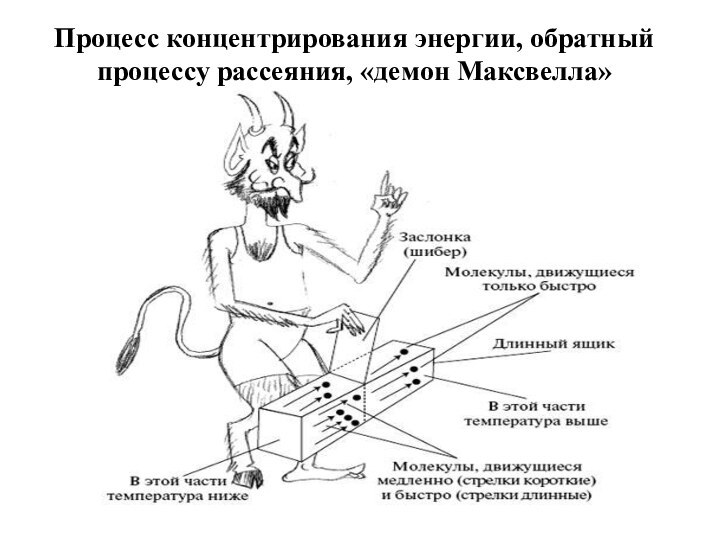
Демон Максвелла — мысленный эксперимент 1867 года, а
также его главный персонаж — воображаемое разумное существо микроскопического
размера, придуманное британским физиком Джеймсом Максвеллом с целью проиллюстрировать кажущийся парадокс Второго начала термодинамики.
Слайд 20
Смысл всех решений: для того, чтобы «демону» «отсортировать»
молекулы (быстрые от медленных) необходимо получить информацию о свойствах
молекулы, но информацию нельзя получить бесплатно, за неё приходиться платить энергией, в результате чего ЭНТРОПИЯ системы повышается на величину, по крайней мере равную её понижению за счёт получения информации.
1 бит информации = 3•10-21 Дж
Слайд 21
Связь энтропии и информации в биологических системах
Слайд 22
Информация (I) – это
возможность установить порядок.
Информация – это
снятие неопределенности знаний о чем-то.
Информация – это информация, это не материя и не энергия (Винер).
Информация – это мера упорядоченности системы.
Информация – это структурно-смысловое разнообразие мира (Эшби).
Информация – это мера сведений, содержащихся в том или ином сообщении.
Информация – это отрицательная энтропия (негэнтропия).
Приобретение информации имеет свою энергетическую цену:
1 бит информации эквивалентен 3•10-21 Дж (Harold, 1986)
Слайд 23
I = log2W = - log2p
W = 1/p,
где
W – число микросостояний
p – вероятность каждого из микросостояний
За единицу количества информации (бит) принимается информация, содержащаяся в достоверном сообщении, когда число исходных возможных состояний равно 2 (W = 2).
I = log22= 1 бит
Слайд 24
S = kБln W
I = log2W
Энтропия системы и
информация о системе являются взаимосвязанными
Энтропия (S) есть недостающая информация
(I) для полного описания системы.
или
Информация (I) есть недостающая энтропия (S), т.е. разность между максимально возможной энтропией системы и той энтропией, которой на самом деле обладает система.
Слайд 25
S(э.е.) = 2,3 • 10-24 I бит
1 э.е.
= 1 кал/град = 4,2 Дж/K
1 бит = 10-24
Дж/K
Соотношение между энтропией и информацией было установлено Бриллюэном и сформулировано в виде негэнтропийного принципа информации.
Но это справедливо только для микроинформации (Imic)
Слайд 26
Микроинформация (Imic) – это информация о реализации в
данный момент одного из возможных микросостояний системы, Imic не
может запоминаться, т.к. одно из микросостояний быстро переходит в другое.
Связана с энтропией соотношением Бриллюэна - S(э.е.) = 2,3 • 10-24 I бит – выполняется принцип эквивалентности I и физической энтропии.
Макроинформация (Imаc) – это информация, которая запоминается. Для перехода Imic → Imаc система должна произвести работу, за счет которой она перейдет в устойчивое состояние, потеряв часть энергии в процессе диссипации. В результате S системы увеличится. Это мера множества запоминаемых состояний.
Слайд 27
В чем состоит отличие биологической информации?
Организм человека
массой 70 кг содержит:
- 7 кг
белков
- 150 г ДНК
- 1013 клеток
I = 1,3 • 1026 бит
Отличие биологической информации – ценность:
1) неизбыточность
2) незаменимость
Слайд 28
Нелинейная неравновесная термодинамика
Слайд 29
Манфред Эйген
Теория добиологической эволюции
Эйген создал модель – «ящик
Эйгена», который имеет полупроницаемые перегородки. В него из среды
поступают дезоксирибонуклеотиды, фосфаты, макроэрги.
В «ящике» идет полимеризация полинуклеотидных цепей, репликация, матричный синтез; репликация идет с ошибками, возникают мутации; идет распад одних и возникновение других цепей.
Введено понятие селекционной ценности информации (Is) - соотношение константы скорости синтеза (Кс) к константе скорости распада (Кр) цепей. Чем выше соотношение Кс/Кр ,тем больше Is данной цепи.
Для существования длинных цепей с количеством звеньев > 100 необходимо возникновение гиперциклов.
Гиперцикл—это способ объединения самовоспроизводящихся макромолекул в замкнутые автокаталитические химические циклы.
Слайд 30
Гиперциклы уже обладают некоторыми
признаками живого:
1)
круговорот веществ и энергии,
2) воспроизведение с наследованием информации,
3) приспособляемость к изменяющимся условиям,
4) гиперциклы подвержены естественному отбору на уровне молекул,
5) гиперцикл, построенный из нуклеиновых кислот и белков-ферментов, обеспечивает отбор макромолекул с объемом информации, достаточным и необходимым для возникновения живой системы.
Это гипотеза о молекулярной эволюции, приведшей к созданию первой живой клетки, использующей генетический код для матричного синтеза белка.
Слайд 31
Каталитическая сеть ферментов, включающая замкнутый цикл (Е1 -
Е15). Из Eigen (1971)
Слайд 32
Наиболее поразительные «жизнеподобные» свойства гиперциклов:
могут развиваться,
проходят
через периоды неустойчивости,
создают все более высокие уровни
организации с нарастающим разнообразием и богатством компонентов и структур.
Новые гиперциклы, сформированные подобным образом, вполне могут составить конкуренцию естественному отбору.
Слайд 33
Илья Пригожин (1917-2003)
Илья Пригожин создал нелинейную неравновесную термодинамику
и ввел понятие диссипативной структуры, т.е. открытой системы, которая
живёт вдали от своего термодинамического равновесия с окружающей средой.
Нобелевская премия по химии была присуждена ученому в 1977 году "за работы по термодинамике необратимых процессов, особенно за теорию диссипативных структур".
Слайд 34
Особенности открытой системы:
1.через
открытую систему непрерывно протекает поток материи и энергии, но
2.
система поддерживает устойчивую форму и обеспечивает это автономно путем самоорганизации.
Чтобы подчеркнуть сосуществование изменений и устойчивости (текучее равновесие), Пригожин ввел термин «диссипативные структуры».
Но не все диссипативные структуры являются живыми системами.
Слайд 35
Диссипативная структура — открытая система, которая существует вдали
от термодинамического равновесия.
Свойства диссипативной структуры:
1) устойчивое состояние в
неравновесной среде на фоне диссипации (рассеивания) энергии, которая поступает извне.
2) неравновесная открытая система.
3) спонтанное появление сложной структуры.
Простым примером такой системы являются:
Ячейки Бенара
Реакция Белоусова-Жаботинского
Слайд 36
Основные положения
теории диссипативных структур:
1) базовые
структуры жизни, которые поддерживают себя в далеком от равновесия устойчивом состоянии и могут развиваться.
2) свойства: а) неравновесность, б) нелинейность,
в) неопределенность, г) устойчивость на определенном временном отрезке.
3) островки порядка в мире беспорядка, поддерживающие и даже повышающие свой порядок за счет увеличения беспорядка в окружающей среде.
4) способны к самоорганизации. Это спонтанное зарождение новых структур и новых форм поведения в далеких от равновесия открытых системах, которые характеризуются появлением внутренних петель обратной связи и математически описываются нелинейными уравнениями.
5) проходят точки бифуркации. Это порог устойчивости, где диссипативная структура может либо разрушиться, либо прорваться к одному из новых состояний порядка. Энтропия приобретает отрицательное значение и система скачком переходит в новое стационарное состояние.
Слайд 37
.
6) По мере удаления
от равновесия диссипативная структура движется от универсального к уникальному,
в направлении богатства и разнообразия.
«В детерминистком мире Ньютона нет места истории и творчеству. В живом мире диссипативных структур история играет важную роль: будущее неопределенно, и эта неопределенность служит основой творчества» (Ф.Копра «Паутина жизни»).
«Сегодня - мир, который мы видим снаружи, и мир, который мы ощущаем внутри, сближаются. Это сближение двух миров, вероятно, одно из наиболее важных культурных событий нашего мира» (И.Пригожин «Порядок из хаоса. Новый диалог человека с Природой»).
Слайд 38
Пример возникновения диссипативной структуры - «ячейки
Бенара».
Ячейки Бенара возникают при
критической разности температур между верхним и нижним слоями жидкости при ее нагревании (жидкость находится в кювете).
Слайд 39
Конвективные ячейки Бенара – пример диссипативной структуры.
В
1900 году была опубликована статья французского исследователя Бенара с
фотографией структуры, по виду напоминавшей пчелиные соты. При нагревании снизу слоя ртути, налитой в плоский широкий сосуд, весь слой неожиданно распадался на одинаковые вертикальные шестигранные призмы, которые впоследствии были названы ячейками Бенара. В центральной части каждой ячейки жидкость поднимается, а вблизи вертикальных граней опускается. Иными словами, в сосуде возникают направленные потоки, которые поднимают нагретую жидкость (с температурой T1) вверх, а холодную (с температурой T2) опускают вниз.
Слайд 40
Эксперимент с силиконовым маслом, разлитым на плоской горячей
поверхности, демонстрирует строго регулярную пространственную структуру с периодичностью, кратной
толщине жидкого слоя. На фотографии видны выходящие из центра и сходящиеся по сторонам шестигранника конвективные потоки масла. На границах соприкасающихся сторон в местах стекания сформированы затененные каналы, свидетельствующие о том, что боковая поверхность тороида криволинейная и не имеет скачкообразных переходов.
Слайд 41
Облака похожи на ячейки Бенара, хотя они из-за
потоков воздуха обладают не столь правильной формой как ячейки
в нагреваемом масле.
Слайд 42
Диссипативная структура на примере роста лишайника.
Слайд 43
Пример самоорганизованных структур
Торнадо. Вихревые диссипативные структуры
Слайд 45
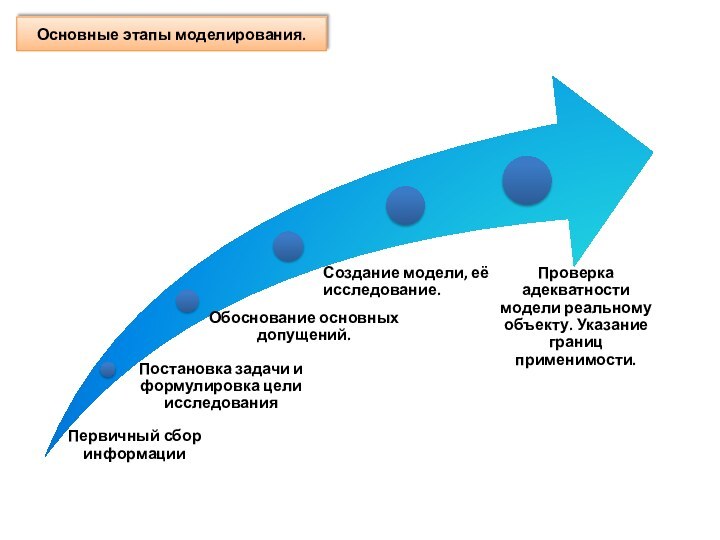
Моделирование.
Моделирование – сознательная замена некоторого
объекта, процесса, явления, вследствие
его сложности, другим
объектом, процессом, явлением, но упрощённым, сохраняющим
основные
наиболее существенные свойства.
Модель – условный образ реального объекта, отражающий признаки объекта, существенные для целей исследования.
Слайд 47
Биологические модели делят на 3 типа:
1)
Биологические (предметные) модели (лабораторные животные, изолированные органы, культуры клеток,
суспензии органелл).
2) Физические (аналоговые) модели – физические системы, обладающие аналогичным с объектом поведением (гидродинамические модели – устройства, имитирующие действие органов: искусственное сердце, почка, аппарат искусственного дыхания).
3) Математические модели – системы математических выражений, описывающие те или иные свойства изучаемого объекта.
Слайд 48
Математические модели. Метод фазовой плоскости.
Современная практика математического моделирования
показала, что
наиболее содержательные математические модели включают, как правило,
два уравнения:
dx/dt
= P (x, y)
dy/dt = Q (x, y)
В процессе изменения состояния системы во времени, переменные х, у
изменяются согласно вышеприведённым уравнениям.
Плоскость с осями координат х и у, на которой каждой точке М с координатами(х, у) соответствует определённое состояние системы, носит название
фазовой плоскости.
Если в момент времени t0 координаты
точки М (х0, у0), в каждый следующий
момент времени t точка будет двигаться в
соответствии с уравнениями и каждый раз
принимать положения М (х, у).
Слайд 49
Типы устойчивости особых точек.
Устойчивый узел на фазовой плоскости.
Неустойчивый
узел на фазовой плоскости.
Устойчивый фокус на фазовой плоскости.
Неустойчивый фокус
на фазовой плоскости.
Седло на фазовой плоскости.
Особая точка «центр» на фазовой плоскости.
Слайд 50
Модель Вольтерра хищник-жертва.
Эта модель отражает численности популяций жертв
(х) и хищников (у),
взаимодействующих друг с другом по механизму
свободных соударений.
Это значит, что численность жертв пропорциональна вероятности встречи их с
хищниками, т. е. пропорциональна ху. Естественная смертность хищников
(-ky). Жертвы размножаются со скоростью, пропорциональной их
численности, в условиях с неограниченным количеством пищи.
Dx/dt = k1х – k2ху
Dу/dt = k3ху – k4у
При различных соотношениях в системе возможно выживание только жертвы, только хищника и сосуществование обоих видов. В этом случае численности видов совершают колебания, причём колебания численности хищника в модели запаздывают по отношению к колебаниям численности жертвы (Рисунок Б).
Слайд 51
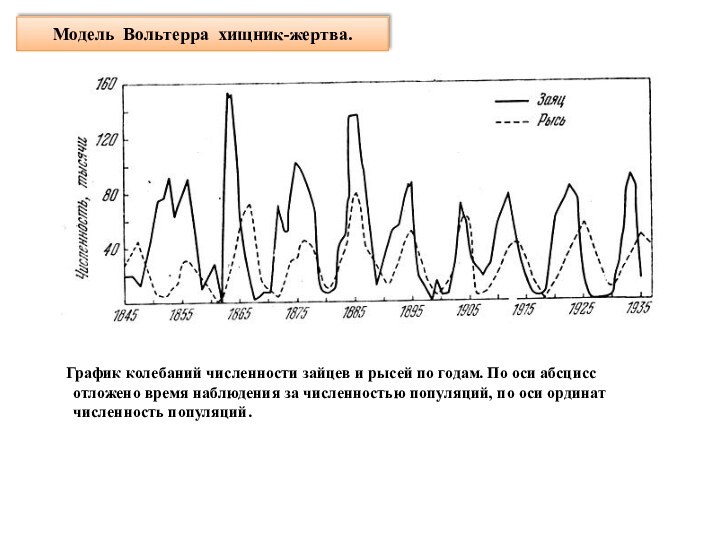
Модель Вольтерра хищник-жертва.
График колебаний численности
зайцев и рысей по годам. По оси абсцисс отложено
время наблюдения за численностью популяций, по оси ординат численность популяций.
Слайд 52
Точка типа «центр» на фазовой плоскости.
Стационарные значения координат
стационарной системы
x = k1 /k2 и у
= k 4/k3
соответствуют особой точке «центр», которая отражает колебания численности популяций.
Слайд 53
Реакция Белоусова-Жаботинского (BZ reaction)
Борис Павлович Белоусов (1893-1970)
Белоусов Борис
Павлович– российский и советский химик и биофизик. Как военный
химик Белоусов занимался разработкой способов борьбы с отравляющими веществами, составами для противогазов, газовыми анализаторами, препаратами, снижающими воздействие радиации на организм.
В 1951 г. при исследовании окисления лимонной кислоты броматом в присутствии катализатора (сульфат церия), обнаружил концентрационные колебания ионов церия (BZ-реакция), т.е. открыл первую колебательную реакцию.
В 1980 г. Б.П. Белоусову посмертно была присуждена Ленинская премия.
Реакция Белоусова-Жаботинского вошла в золотой фонд науки XX века.
Слайд 54
Анатолий Маркович Жаботинский
(1938 — 2008)
Жаботинский Анатолий Маркович
– cоветский биофизик, физико-химик. Один из основателей нелинейной химической
динамики, исследовал и описал с помощью математической модели реакцию Белоусова-Жаботинского, лауреат Ленинской премии (1980). С 1991 года работал в США.
Реакция Белоусова-Жаботинского стала базовой моделью для
исследования процессов самоорганизации, включая образование неоднородных распределений концентраций реагирующих веществ, распространение пятен (patches), спиральных волн и других автоволновых процессов.
Она исследована в сотнях лабораторий мира в сосудах различной формы, в протоке, на пористых средах, при различных воздействиях – изменении температуры, световом и радиационном воздействии.
Слайд 55
А. Н. Заикин, Г. Р. Иваницкий, А. М.
Жаботинский, В. И. Кринский — лауреаты Ленинской премии. Апрель
1980 г.
Слайд 56
Реакция Белоусова-Жаботинского. Упрощённая схема
Слайд 57
Реакция Белоусова-Жаботинского.
Ниже представлена сложная структура
реакции:
Слайд 58
Изменение цвета реакционной смеси в реакции Белоусова – Жаботинского
(«химический маятник», модель автоколебательных процессов)
Слайд 59
Одна из первых осциллограмм периодической реакции, полученная Б.П. Белоусовым
Класс
реакций Белоусова служит удобной моделью для изучения колебательных и
волновых процессов в активных средах. Сюда относятся:
периодические процессы клеточного метаболизма;
2) волны активности в сердечной ткани и ткани мозга;
3) процессы, происходящие на уровне морфогенеза и на уровне экологических систем.
Слайд 60
Различные пространственные режимы в реакции Белоусова-Жаботинского
Слайд 61
1.Можно ли с помощью внешних воздействий влиять на
самоорганизацию во времени и пространстве?
Воздействия:
а) изменение скорости
притока конечных и промежуточных веществ в сферу реакции,
б) различные режимы освещения,
в)радиоактивное облучение.
Такие исследования имеют большой практический смысл. Они позволяют находить способы управления автоволновой активностью и помогают искать режимы воздействия на спиральные волны в активной ткани сердца, распад которых приводит к фибрилляциям.
Слайд 62
C помощью BZ реакции можно моделировать большое разнообразие
процессов, в том числе формирование спиральных волн – в
терминологии кардиологов – реентри (re-entry), появление которых в миокарде связывают с фибрилляциями и различными
аритмиями – опасными сердечными заболеваниями
Слайд 63
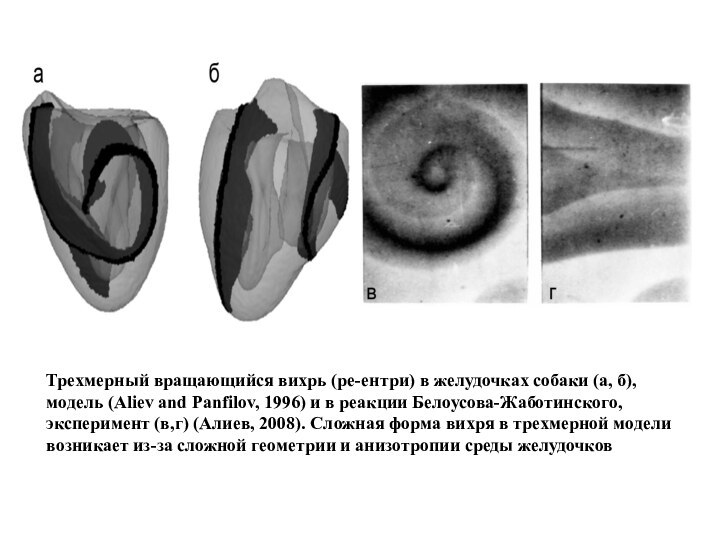
Трехмерный вращающийся вихрь (ре-ентри) в желудочках собаки (а,
б), модель (Aliev and Panfilov, 1996) и в реакции
Белоусова-Жаботинского, эксперимент (в,г) (Алиев, 2008). Сложная форма вихря в трехмерной модели возникает из-за сложной геометрии и анизотропии среды желудочков
Слайд 64
Мерцательная аритмия (мерцание предсердий, фибрилляция предсердий) — аритмия, при
которой по предсердиям постоянно и беспорядочно циркулируют волны возбуждения, вызывающие
хаотические сокращения отдельных мышечных волокон предсердий. Стенки предсердий не сокращаются ритмично, а «мерцают», как пламя на ветру.
Слайд 65
Полосы на шкуре тигра вызваны близкими к реакции
Белоусова—Жаботинского колебательными биохимическими реакциями с диффузией, существование которых предположил
математик
Алан Тьюринг.
Слайд 66
Процесс концентрирования энергии, обратный процессу рассеяния, «демон Максвелла»