Презентация на тему Центр тяжести. (Тема 1.6)

через которую проходит линия действия их равнодействующей при любом

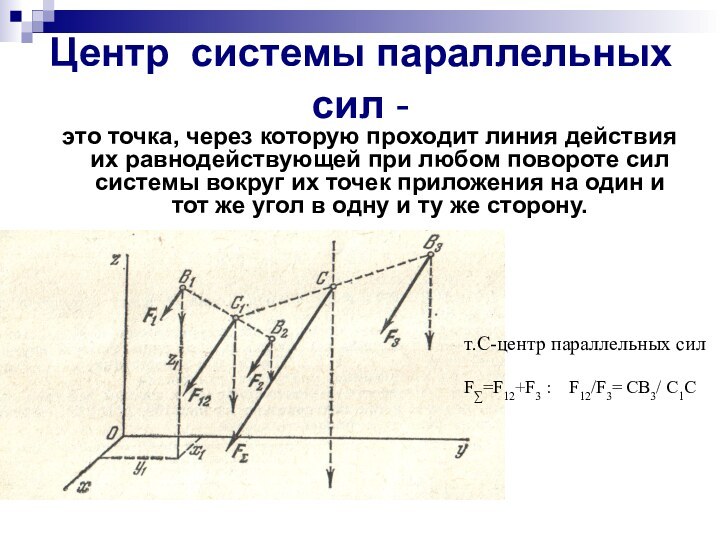
повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону.

т.С-центр параллельных сил

F∑=F12+F3 : F12/F3= CВ3/ С1C

Пространственная система n параллельных сил и

равнодействующая этой системы

F2

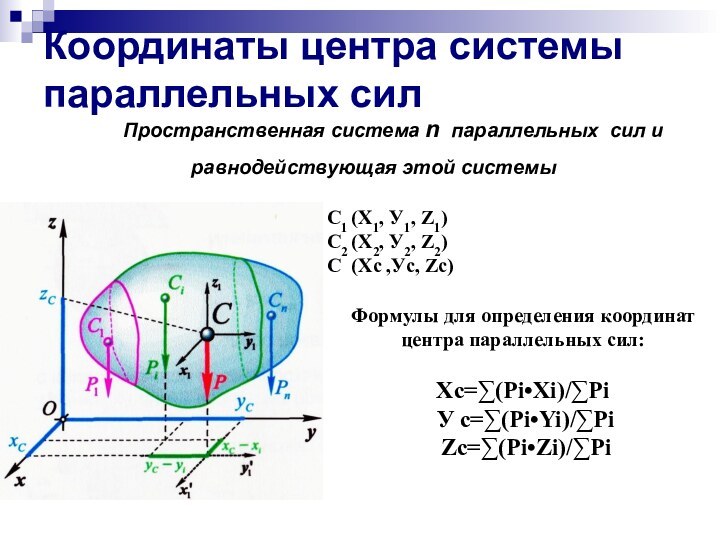
Формулы для определения координат центра параллельных сил:

Xc=∑(Рi•Xi)/∑Рi
У c=∑(Рi•Yi)/∑Рi
Zc=∑(Рi•Zi)/∑Рi

С1 (Х1, У1, Z1)
С2 (Х2, У2, Z2)
C (Хc ,Уc, Zc)

тела- сила, с которой тело притягивается к земле.
Любое

тело можно представить в виде элементарных частиц, которые имеют определенный вес.
Сила тяжести каждой элементарной частицы направлена к центру земли и образует систему параллельных сил.
Таким образом центр тяжести тела- есть цент параллельных сил тяжести всех элементарных частиц тела.
Центр тяжести- геометрическая точка, которая может быть расположена в самом теле или вне тела( цилиндр с отверстием).
В этой точке условно считают сосредоточенным вес всего тела.

ромб, параллелограмм) - центр тяжести в точке пересечения диагоналей.

лежит на пересечении медиан (на расстоянии 1/3 высоты от

каждого основания)

в точке с координатами:

а) Xc= R, Уc=4R/3π (рис. а)
б) Xc=4R/3π , Уc=R (рис. б)

пирамида — центр тяжести на высоты от основания

в точке с координатами Xc =0,

Уc=h/2

с координатами

где h — высота швеллера;

Z0 — расстояние от центра тяжести и оси Уc до наружной грани стенки

точке с координатами

метод используется для определения центра тяжести однородных симметричных тел

и симметричных плоских фигур.
Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси
Если две оси симметрии, то центр тяжести находится в точке их пересечения.
Центр тяжести тела вращения лежит на оси вращения.

неправильную геометрическую форму, то центр тяжести такой фигуры можно

определить двумя способами:
1) практическим методом - подвешивания фигуры на острие;
2) теоретическим методом

том, что тело разбивают на фигуры простейшей геометрической формы.

Затем определяется положение центра тяжести и площади каждой элементарной фигуры. Для того чтобы найти координаты центра тяжести заданной сложной фигуры, используются следующие формулы:






Где Ai — площади элементарных фигур, на которые разбита сложная фигура;
Xi, Yi— координаты центра тяжести каждой элементарной фигуры относительно случайных осей x и у.

тело имеет полости или плоская фигура вырезы, то тело

вначале рассматривают как единое целое, а затем при подстановке в формулы полости и вырезы будем подставлять со знаком минус.