Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Виды поляризации

Содержание

Поляризация светаСогласно теории Максвелла, свет представляет собой поперечные электромагнитные колебания. Возможны различные типы таких колебаний в зависимости от ориентации светового вектора – вектора напряжённости электрического поля Е
Лекции по физике. ОптикаПоляризация света. Законы теплового излучения Поляризация светаСогласно теории Максвелла, свет представляет собой поперечные электромагнитные колебания. Возможны различные Поляризация светаЕсли в волнах, составляющих световой пучок с одинаковой вероятностью встречаются различные Поляризация светаИз естественного света можно выделить волны, в которых колебания светового вектора Поляризация светаВ эллиптически поляризованной волне конец светового вектора описывает эллипсПри циркулярной (круговой) Поляризация светаРазличают правую и левую круговую и эллиптическую поляризации. В первом случае Поляризация светаСтепенью поляризации называется величина: где Imax и Imin – соответственно максимальная и Поляризация светаЕстественно поляризованный свет можно преобразовать в поляризованный с помощью поляризаторов – Поляризация светаВ качестве поляризаторов можно использовать естественные анизотропные кристаллы: исландский шпат, турмалин Поляризация светаЧтобы разделить лучи с разным состоянием поляризации используют не просто двулучепреломляющие Поляризация светаКристаллы турмалина действуют иначе чем исландский шпат. Они имеют различный коэффициент Изменение состояния поляризации при отражении/преломленииУстановлено, что соотношение интенсивностей отражённых/преломлённых лучей на границе Изменение состояния поляризации при отражении/преломленииКоэффициент отражения света, поляризованного перпендикулярно плоскости падения монотонно Поляризация светаВеличина угла Брюстера определяется соотношением: tgϕБ=n где n – относительный Закон МалюсаЕсли на пути луча естественного света установить два поляризатора и исследовать Искусственная оптическая анизотропияЯвление искусственной оптической анизотропии заключается в том, что оптически изотропные Вращение плоскости поляризацииНекоторые вещества (сахар, кварц, скипидар и др.), называемые оптически активными Вращение плоскости поляризацииДля кристаллов и чистых жидкостей: ϕ=αdДля растворов: ϕ=αСdРазделяют право- и левовращающие Применение поляризации светаИсследования в поляризованном свете имеют большое техническое значениеНа моделях деталей Тепловое излучениеНагретые тела излучают электромагнитные волны. При достаточно высокой температуре тел (свыше Тепловое излучениеЭта величина зависит также от температуры R(ν,T)Каждое вещество обладает также характерной Тепловое излучениеКак и R(ν,T) А(ν,T) зависит от частоты и температурыАбсолютно чёрное тело Законы теплового излученияВ замкнутой системе нагретые тела должны находиться в равновесии со Законы теплового излученияСогласно закону Стефана-Больцмана интегральная энергетическая светимость абсолютно чёрного тела Re Законы теплового излученияСогласно закону смещения Вина зависимость длины волны λmax, соответствующей максимуму Законы теплового излученияИспользуя термодинамический подход можно получить следующую формулу для функции r(ν,T) Законы теплового излученияВыражение (1) находится в противоречии с опытными данными и с Конец лекции
Слайды презентации

Слайд 2 Поляризация света
Согласно теории Максвелла, свет представляет собой поперечные

Поляризация светаСогласно теории Максвелла, свет представляет собой поперечные электромагнитные колебания. Возможны

электромагнитные колебания. Возможны различные типы таких колебаний в зависимости

от ориентации светового вектора – вектора напряжённости электрического поля Е

Слайд 3 Поляризация света
Если в волнах, составляющих световой пучок с

Поляризация светаЕсли в волнах, составляющих световой пучок с одинаковой вероятностью встречаются

одинаковой вероятностью встречаются различные направления светового вектора то такой

свет называется естественным
Если в световом пучке существует направление преимущественной ориентации светового вектора, то такой свет называется частично поляризованным

Слайд 4 Поляризация света
Из естественного света можно выделить волны, в

Поляризация светаИз естественного света можно выделить волны, в которых колебания светового

которых колебания светового вектора происходят в одной плоскости. Такой

свет называют плоскополяризованным или линейно поляризованным
При сложении двух линейно-поляризованных колебаний в общем случае получается эллиптически поляризованная волна, частным случаем которой является циркулярно поляризованное колебание

Слайд 5 Поляризация света
В эллиптически поляризованной волне конец светового вектора

Поляризация светаВ эллиптически поляризованной волне конец светового вектора описывает эллипсПри циркулярной

описывает эллипс
При циркулярной (круговой) поляризации конец светового вектора описывает

окружность. Циркулярно поляризованную волну можно представить как сумму двух линейно поляризованных колебаний одинаковой амплитуды происходящих в перпендикулярных друг другу плоскостях и сдвинутых по фазе на угол ±π/2

Слайд 6 Поляризация света

Различают правую и левую круговую и эллиптическую

Поляризация светаРазличают правую и левую круговую и эллиптическую поляризации. В первом

поляризации. В первом случае конец светового вектора вращается по

часовой стрелке, а во втором случае против часовой стрелки

Слайд 7 Поляризация света
Степенью поляризации называется величина:



где Imax и Imin

Поляризация светаСтепенью поляризации называется величина: где Imax и Imin – соответственно максимальная

– соответственно максимальная и минимальная интенсивности линейно поляризованных компонент

волны
Для естественного и циркулярно-поляризованного света Р=0, а для плоскополяризованного Р=1

Слайд 8 Поляризация света
Естественно поляризованный свет можно преобразовать в поляризованный

Поляризация светаЕстественно поляризованный свет можно преобразовать в поляризованный с помощью поляризаторов

с помощью поляризаторов – устройств, пропускающих колебания, имеющие преимущественное

направление светового вектора
В поляризаторах используют два эффекта:
Различие коэффициентов пропускания
Различие в отражении/преломлении колебаний с различной поляризацией

Слайд 9 Поляризация света
В качестве поляризаторов можно использовать естественные анизотропные

Поляризация светаВ качестве поляризаторов можно использовать естественные анизотропные кристаллы: исландский шпат,

кристаллы: исландский шпат, турмалин и др.
В кристалле исландского шпата

показатель преломления лучей с разной поляризацией различен (двулучепреломление), поэтому при прохождении сквозь кристалл происходит их пространственное разделение

Слайд 10 Поляризация света
Чтобы разделить лучи с разным состоянием поляризации

Поляризация светаЧтобы разделить лучи с разным состоянием поляризации используют не просто

используют не просто двулучепреломляющие кристаллы, а их комбинации –

поляризационные призмы
Призма Николя состоит из двух склеенных между собой кристаллов исландского шпата, определённой формы и кристаллографической ориентации. Один из лучей выводится в сторону благодаря полному внутреннему отражению от прослойки, соединяющей кристаллы

Слайд 11 Поляризация света
Кристаллы турмалина действуют иначе чем исландский шпат.

Поляризация светаКристаллы турмалина действуют иначе чем исландский шпат. Они имеют различный

Они имеют различный коэффициент поглощения лучей разной поляризации (дихроизм).

Поэтому после прохождения кристалла интенсивность одного из лучей оказывается выше чем другого
Можно изготовить полимерные материалы, обладающие таким же свойством

Слайд 12 Изменение состояния поляризации при отражении/преломлении
Установлено, что соотношение интенсивностей

Изменение состояния поляризации при отражении/преломленииУстановлено, что соотношение интенсивностей отражённых/преломлённых лучей на

отражённых/преломлённых лучей на границе двух диэлектриков различно для волн

различной поляризации
Различают луч, поляризованный в плоскости падения и перпендикулярно к ней. В первом случае световой вектор лежит в плоскости, проходящей через перпендикуляр к поверхности раздела двух сред и падающий луч

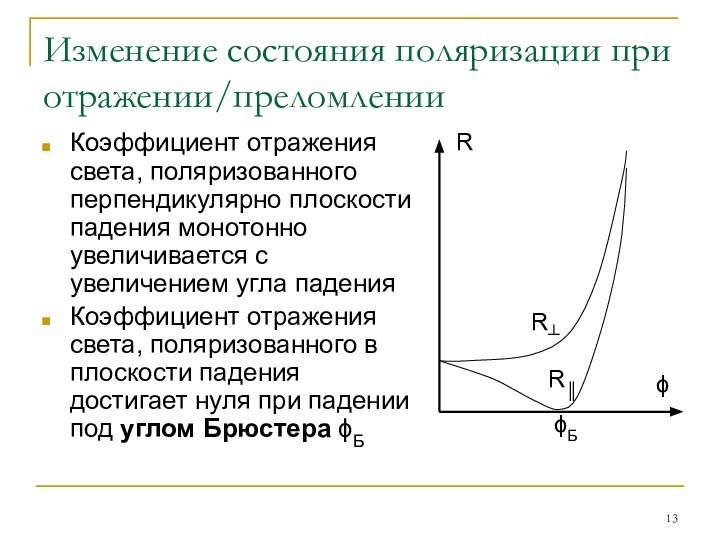
Слайд 13 Изменение состояния поляризации при отражении/преломлении
Коэффициент отражения света, поляризованного

Изменение состояния поляризации при отражении/преломленииКоэффициент отражения света, поляризованного перпендикулярно плоскости падения

перпендикулярно плоскости падения монотонно увеличивается с увеличением угла падения
Коэффициент

отражения света, поляризованного в плоскости падения достигает нуля при падении под углом Брюстера ϕБ

Слайд 14 Поляризация света
Величина угла Брюстера определяется соотношением:

Поляризация светаВеличина угла Брюстера определяется соотношением: tgϕБ=n где n – относительный

tgϕБ=n
где n – относительный показатель преломления двух сред
Изменение состояния

поляризации при отражении/преломлении используется для создания поляризаторов света
Стопа Столетова представляет собой 8-10 стеклянных пластинок устанавливаемых под углом Брюстера. Она даёт практически полную поляризацию падающего и прошедшего лучей

Слайд 15 Закон Малюса
Если на пути луча естественного света установить

Закон МалюсаЕсли на пути луча естественного света установить два поляризатора и

два поляризатора и исследовать зависимость интенсивности I прошедшего света

от угла α между осями поляризаторов, то можно получить закон Малюса:
I=I0cos2α
где I0 – интенсивность падающего света

Слайд 16 Искусственная оптическая анизотропия
Явление искусственной оптической анизотропии заключается в

Искусственная оптическая анизотропияЯвление искусственной оптической анизотропии заключается в том, что оптически

том, что оптически изотропные вещества становятся анизотропными в результате

внешних воздействий: сжатия/растяжения, наложения электрического (эффект Керра) и магнитного полей

Слайд 17 Вращение плоскости поляризации
Некоторые вещества (сахар, кварц, скипидар и

Вращение плоскости поляризацииНекоторые вещества (сахар, кварц, скипидар и др.), называемые оптически

др.), называемые оптически активными обладают способностью поворачивать плоскость поляризации

проходящего сквозь них света
Величина угла поворота ϕ пропорциональна расстоянию d, пройденному светом в веществе и концентрации С раствора в случае растворов. Коэффициент пропорциональности α называется удельным вращением

Слайд 18 Вращение плоскости поляризации
Для кристаллов и чистых жидкостей:
ϕ=αd
Для растворов:

Вращение плоскости поляризацииДля кристаллов и чистых жидкостей: ϕ=αdДля растворов: ϕ=αСdРазделяют право- и

ϕ=αСd
Разделяют право- и левовращающие оптически активные вещества
Под действием

магнитного поля оптически неактивные вещества могут становиться оптически активными. Это явление называется эффектом Фарадея

Слайд 19 Применение поляризации света
Исследования в поляризованном свете имеют большое

Применение поляризации светаИсследования в поляризованном свете имеют большое техническое значениеНа моделях

техническое значение
На моделях деталей из материалов с искусственной анизотропией

можно выявлять участки на которые приходится наибольшая нагрузка
Поляризационные устройства позволяют управлять световыми потоками, записывать информацию, проводить оптические исследования и измерения физических параметров

Слайд 20

Слайд 21 Тепловое излучение
Нагретые тела излучают электромагнитные волны. При достаточно

Тепловое излучениеНагретые тела излучают электромагнитные волны. При достаточно высокой температуре тел

высокой температуре тел (свыше 500 0С) наблюдается их свечение

в видимом диапазоне
Для каждого вещества характерна своя зависимость мощности излучения с единичной площади, отнесённая к частотному интервалу от частоты (или длины волны) – спектральная плотность энергетической светимости R

Слайд 22 Тепловое излучение
Эта величина зависит также от температуры R(ν,T)
Каждое

Тепловое излучениеЭта величина зависит также от температуры R(ν,T)Каждое вещество обладает также

вещество обладает также характерной для него способностью поглощать падающее

излучение. Это свойство характеризуется величиной спектральной поглощательной способности А(ν,T), показывающей какая доля мощности излучения падающего на единицу площади поглощается телом. Эта мощность так же должна быть отнесена к малому спектральному интервалу в пределах которого производится облучение

Слайд 23 Тепловое излучение
Как и R(ν,T) А(ν,T) зависит от частоты

Тепловое излучениеКак и R(ν,T) А(ν,T) зависит от частоты и температурыАбсолютно чёрное

и температуры
Абсолютно чёрное тело поглощает всё падающее на него

излучение. Для него А(ν,T)=1
Моделью абсолютно чёрного тела может служить небольшое отверстие в теле, содержащем замкнутую полость

Слайд 24 Законы теплового излучения
В замкнутой системе нагретые тела должны

Законы теплового излученияВ замкнутой системе нагретые тела должны находиться в равновесии

находиться в равновесии со своим излучением. Из этого факта

следует, что между способностью тел излучать и поглощать свет должно существовать фундаментальное соотношение (закон Кирхгофа):



где r(ν,T) - спектральная плотность энергетической светимости абсолютно чёрного тела

Слайд 25 Законы теплового излучения
Согласно закону Стефана-Больцмана интегральная энергетическая светимость

Законы теплового излученияСогласно закону Стефана-Больцмана интегральная энергетическая светимость абсолютно чёрного тела

абсолютно чёрного тела Re пропорциональна четвёртой степени его термодинамической

температуры:
Re=σT4
где σ - постоянная Стефана-Больцмана
Функция r(ν,T) – имеет максимум, положение которого зависит от температуры тела

Слайд 26 Законы теплового излучения
Согласно закону смещения Вина зависимость длины

Законы теплового излученияСогласно закону смещения Вина зависимость длины волны λmax, соответствующей

волны λmax, соответствующей максимуму функции r(ν,T), от температуры тела

описывается формулой:
λmax=b/T
где b – постоянная Вина

Слайд 27 Законы теплового излучения
Используя термодинамический подход можно получить следующую

Законы теплового излученияИспользуя термодинамический подход можно получить следующую формулу для функции

формулу для функции r(ν,T) (Формула Рэлея-Джинса):

(1)
Эта формула показывает, что

интегральная излучательная способность Re=∞ т.к. интеграл от (1) расходится

Слайд 28 Законы теплового излучения
Выражение (1) находится в противоречии с

Законы теплового излученияВыражение (1) находится в противоречии с опытными данными и

опытными данными и с законом Стефана-Больцмана. Этот результат получил

название «ультрафиолетовой катастрофы» т.к. он показал, что в рамках классической физики невозможно объяснить законы теплового излучения

Слайд 29

  • Имя файла: vidy-polyarizatsii.pptx
  • Количество просмотров: 155
  • Количество скачиваний: 0
- Предыдущая шар цилиндр конус
Следующая - Подростковый возраст

Похожие презентации

Сила упругости Сила упругости 143
Движение и сила Движение и сила 192
Comparison of Competitors’ Evaporative Light Scattering Detectors Comparison of Competitors’ Evaporative Light Scattering Detectors 169
Презентация по физике на тему : Материал для подготовке научных работ Презентация по физике на тему : Материал для подготовке научных работ 143
Сила физика Сила физика 369
Цепь Цепь 143
Модели негауссовых случайных блужданий с конечной дисперсией Модели негауссовых случайных блужданий с конечной дисперсией 157
Подготовка к ЕГЭ Электродинамика Подготовка к ЕГЭ Электродинамика 242
Кинетическая и потенциальная энергия Кинетическая и потенциальная энергия 136
Теоретические основы ИК-спектроскопии и применение в фармации Теоретические основы ИК-спектроскопии и применение в фармации 149
Испарение. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара Испарение. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара 150
Гидравлические машины Гидравлические машины 212
Презентация по физике на тему Плавление и отвердевание вещества 8 класс Презентация по физике на тему Плавление и отвердевание вещества 8 класс 131
Солнечные батареи Солнечные батареи 145
Преломление света физика Преломление света физика 132
Задачи и ответы по физике Задачи и ответы по физике 155
Бытовая техника Бытовая техника 132
Период полураспада. Закон радиоактивного распада Период полураспада. Закон радиоактивного распада 116
Радиолокация Радиолокация 200
Температурные шкалы и их модели Температурные шкалы и их модели 141
Кристаллические и аморфные тела Кристаллические и аморфные тела 129
Презентация Диссипативные структуры в вязкой жидкости Презентация Диссипативные структуры в вязкой жидкости 139
Плазма Плазма 112
Экономия электроэнергии в школе Экономия электроэнергии в школе 145
Электростатика 10-11 класс Электростатика 10-11 класс 189
Презентация Физические олимпиады школьников Презентация Физические олимпиады школьников 179
Ускорение свободного падения в условиях Крайнего Севера Ускорение свободного падения в условиях Крайнего Севера 120
Закон всемирного тяготения Закон всемирного тяготения 124
Трансформатор Трансформатор 125
Техническая механика Техническая механика 169