- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Волны в среде
Содержание
- 2. Вступление Если в каком-нибудь месте
- 3. Механические волны Механические волны бывают
- 4. Если смещение частиц среды
- 5. Особенность Характерной особенностью механических волн
- 6. В этой модели инертные
- 7. Если в одномерной модели
- 8. Если механическая
- 9. В стоячей волне нет потока
- 10. При распространении
- 11. Презентацию выполнил Ученик 10 Б классаТутаев АлександрГеннадьевич
- 12. Скачать презентацию
- 13. Похожие презентации
Вступление Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний











Слайд 3
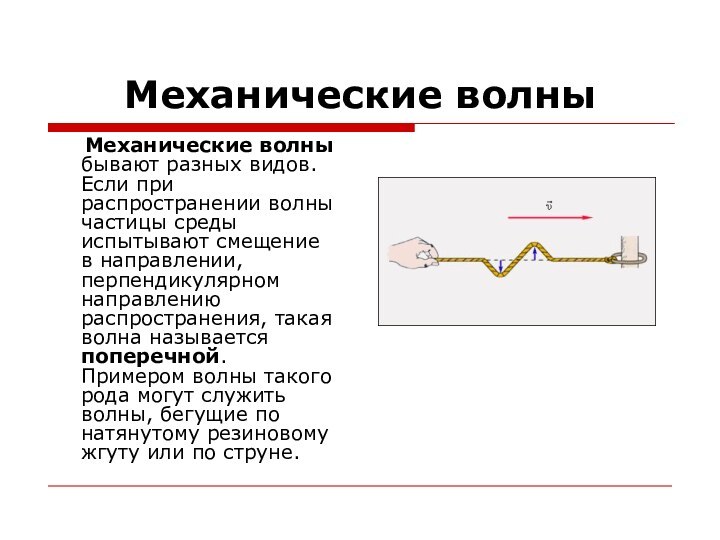
Механические волны
Механические волны бывают разных
видов. Если при распространении волны частицы среды испытывают смещение
в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне.Слайд 4 Если смещение частиц среды происходит
в направлении распространения волны, такая волна называется продольной. Волны
в упругом стержне или звуковые волны в газе являются примерами таких волн.
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Слайд 5
Особенность
Характерной особенностью механических волн является
то, что они распространяются в материальных средах (твердых, жидких
или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок.Слайд 6 В этой модели инертные и
упругие свойства разделены. Шарики обладают массой m, а пружинки
– жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных
Слайд 7 Если в одномерной модели твердого
тела один или несколько шариков сместить в направлении, перпендикулярном
цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появляется. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.
Слайд 8 Если механическая волна,
распространяющаяся в среде, встречает на своем пути какое-либо препятствие,
то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.
Слайд 9 В стоячей волне нет потока энергии.
Колебательная энергия, заключенная в отрезке струны между двумя соседними
узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота струна обладает бесчисленным количеством собственных (резонансных) частот fn. На рис. изображены несколько типов стоячих волн в струне, закреплённой на обоих концах.В соответствии с принципом суперпозиции стоячие волны различных типов (то есть с разными значениями n) могут одновременно присутствовать в колебаниях струны.
Слайд 10 При распространении бегущей
волны возникает поток энергии, пропорциональный скорости волны и квадрату
ее амплитуды.Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы μ (то есть массы единицы длины) и силы натяжения T:
Скорость распространения продольных волн в безграничной среде определяется плотностью среды ρ (то есть массой единицы объема) и модулем всестороннего сжатия B, который равен коэффициенту пропорциональности между изменением давления Δp и относительным изменением объема ΔV / V, взятому с обратным знаком:
Выражение для скорости распространения продольных волн в безграничных средах имеет вид
Например, при температуре 20 °С скорость распространения продольных волн в воде υ ≈ 1480 м/с, в различных сортах стали υ ≈ 5–6 км/с.
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия B входит модуль Юнга E:
Для стали отличие E от B невелико, для других материалов оно может составлять 20–30 % и даже больше.





























