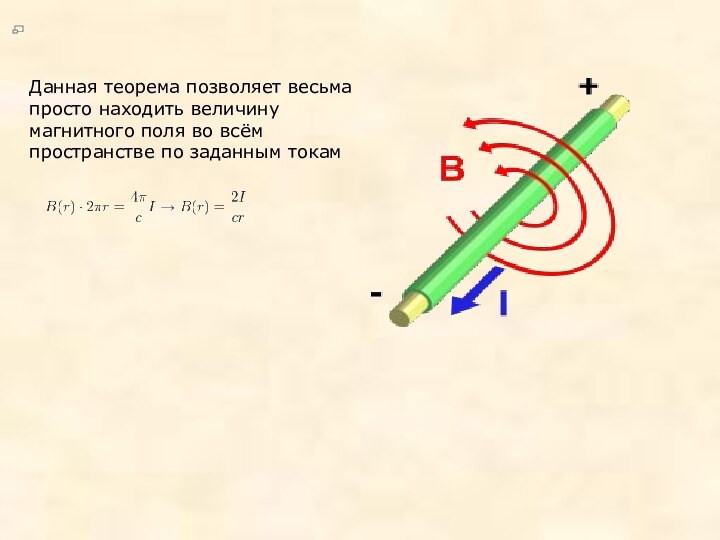
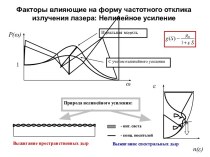
с током на магнитную стрелку является движущееся электричество; магнетизм—лишь
одно из его многочисленных проявлений. Не проводник, по которому течет ток, становится магнитом, а наоборот, магнит представляет собой совокупность токов. В магните есть множество элементарных круговых токов, текущих в плоскостях, перпендикулярных к его оси.Андре-Мари Ампер высказал гениальную идею: единственной причиной действия проводника с током на магнитную стрелку является движущееся электричество; магнетизм—лишь одно из его многочисленных проявлений. Не проводник, по которому течет ток, становится магнитом, а наоборот, магнит представляет собой совокупность токов. В магните есть множество элементарных круговых токов, текущих в плоскостях, перпендикулярных к его оси.
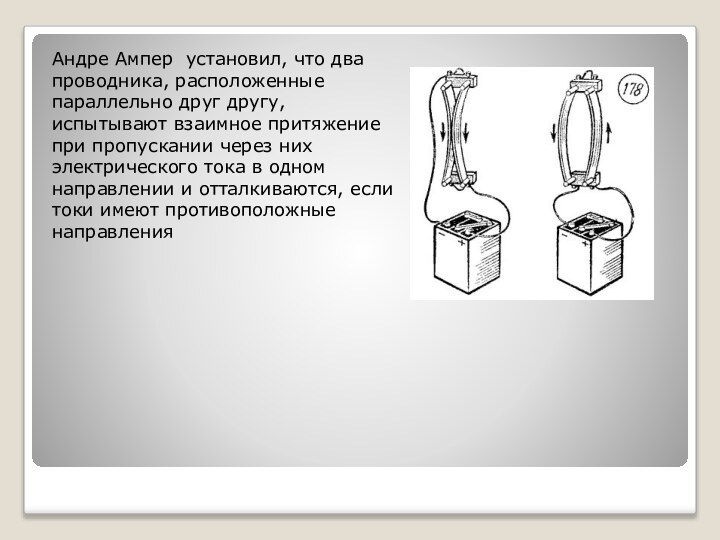
АВ — неподвижный проводник, ECDF — подвижный проводник, укрепленный на стеклянной оси EF.
Для зашиты от воздушных колебаний прибор накрыт стеклянным колпаком. (Рисунок Ампера).






![Закон Ампера В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]: Здесь — вектор](/img/tmb/11/1082877/3e23527ffa870da0b81bf5a5e989cccc-720x.jpg)
![Закон Ампера Тогда теорема о циркуляции запишется в форме[6] где под](/img/tmb/11/1082877/6673e9ad1e004f6b1fdd152261d09db7-720x.jpg)