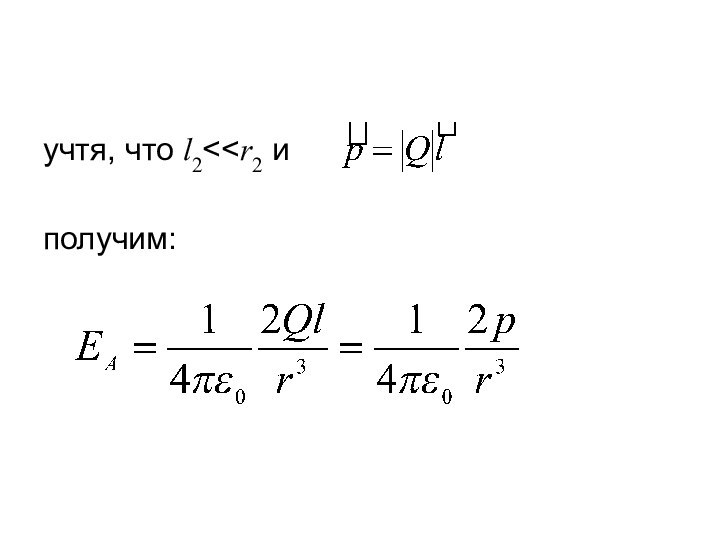пара, ауд. 1411
Практика и лабораторные
суббота 3-я пара ауд. 1402
ДЦАС-1-1,
I неделя,ДЦИМ -1-1, II неделя,
вторник ДЦИС-1-1, I неделя, 3-я пара ауд. 1402
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Заряд
Содержание
- 2. Лекции – ДЦ(АС,ИС, ИМ) - 1 каждый
- 3. 1. Электростатическое поле и его характеристики 1.1. Электрический заряд и закон его сохранения.
- 4. Примеры обнаружения явления статического электричества и электростатического
- 5. Было обнаружено, что часть заряженных тел притягивается,
- 6. 1.1.2.Свойства электрического заряда. Единица электрического заряда
- 7. Элементарный электрический заряд существует в двух видах.
- 8. Свойства электрического заряда Все тела в природе
- 9. Закон сохранения электрического заряда:алгебраическая сумма электрических зарядов
- 10. 1.2. Закон кулона1.2.1. Понятие точечного заряда.Для описания взаимодействия
- 11. 1.2.2. Эмпирическая природа открытия закона Кулона.Силы взаимодействия
- 12. Формулировка закона Кулона Сила взаимодействия F между
- 13. Векторная форма закона Кулона. Сила F направлена
- 14. Силы кулоновского взаимодействия и III закон Ньютона.
- 15. Электрическая постоянная ε0=8,85×10-12 Кл2/(Н⋅м2)ε0=8,85×10-12 Ф/м =9×109 (Н⋅м2)/Кл2= 9×109 м/Ф
- 16. Экспериментальная проверка закона Кулона на макро и
- 17. Физических смысл величин в законе Кулона Из
- 18. Напряженность электростатического поля. Электрический заряд создает электрическое
- 19. Электромагнитные поля распространяются в пространстве со скоростью
- 20. Для обнаружения и опытного исследования электростатического поля
- 21. Напряженность электростатического поля в данной
- 22. Отношение не зависит от Q0 и характеризует
- 23. Напряженность поля точечного заряда в вакууме подставив в формулу определения напряженности закон Кулона получим
- 24. Направление вектора Е совпадает с направлением силы,
- 25. Графическое изображение электростатических полей. Линии, касательные к
- 26. Так как в каждой данной точке пространства
- 27. Линии напряженности электростатического поля начинаются на положительных
- 28. Линии напряженности электростатического поля для двух одинаковых по модулю одноименных и разноименных точечных зарядов.
- 29. Системы из двух положительных и двух отрицательных точечных зарядов (заряды по модулю одинаковы).
- 30. Принцип суперпозиции электростатических полей Рассмотрим систему неподвижных
- 31. Согласно определению напряженности получим
- 32. Эта формула выражает принцип суперпозиции (наложения) электростатических
- 33. Рассмотрим пример применения принципа
- 34. Отметим, что принцип суперпозиции является обобщением опытных
- 35. Поле электрического диполя в вакууме Электрический диполь
- 36. Вектор совпадающий по направлению с плечом диполя
- 37. Применяя принцип суперпозиции электростатических полей, напряженность Е
- 38. Рассмотрим два случая 1. Напряженность поля на
- 39. Обозначив расстояние от точки А до середины оси диполя через r, используя соотношение получим
- 40. учтя, что l2
- 41. 2-й случай. Напряженность поля на перпендикуляре, восстановленном к оси из его середины, в точке В.
- 42. Точка В равноудалена от зарядов,
- 43. Из подобия равнобедренных треугольников, опирающихся
- 44. Скачать презентацию
- 45. Похожие презентации
Лекции – ДЦ(АС,ИС, ИМ) - 1 каждый вторник, 2-ая пара, ауд. 1411Практика и лабораторныесуббота 3-я пара ауд. 1402ДЦАС-1-1, I неделя,ДЦИМ -1-1, II неделя, вторник ДЦИС-1-1, I неделя, 3-я пара ауд. 1402
Слайд 2 Лекции – ДЦ(АС,ИС, ИМ) - 1 каждый вторник, 2-ая
пара, ауд. 1411
I неделя,ДЦИМ -1-1, II неделя,
вторник ДЦИС-1-1, I неделя, 3-я пара ауд. 1402
Слайд 3
1. Электростатическое поле и его характеристики
1.1. Электрический заряд и
закон его сохранения.
Слайд 4 Примеры обнаружения явления статического электричества и электростатического взаимодействия
а. Возникновение притяжения при причесывании. Волосы прилипают к расческе.
б.
Возникновение «прилипания» двух кусков синтетической ткани в. Натирание стекла шелком.
г. Натирание шестью эбонитового стержня.
Слайд 5 Было обнаружено, что часть заряженных тел притягивается, а
часть отталкивается.
Выбор знака заряда был произвольным. Бенджамин Франклин
предложил различать заряженные тела как положительные и отрицательные. Заряд на стекле договорились считать положительным, а на эбоните отрицательным.
В ходе экспериментов обнаружили, что тела, заряженные одноименным знаком отталкиваются, а разноименным притягиваются.
Слайд 6
1.1.2.Свойства электрического заряда.
Единица электрического заряда Кулон (Кл).
В СИ эта единица производная.
Заряд существует в двух видах.
Тела, заряженные одноименным знаком отталкиваются, а разноименным притягиваются.Электрический заряд инвариантен. Его величина не зависит от системы отсчета, т.е. не зависит от того движется он или покоится.
Электрический заряд дискретен. Заряд не может уменьшаться до бесконечно малого значения, Заряд любого тела представляет собой кратное от наименьшего электрического заряда – элементарного заряда.
Электрический заряд аддитивен. Заряд системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему.
Слайд 7 Элементарный электрический заряд существует в двух видах. Элементарный
положительный электрический заряд равен элементарному отрицательному электрическому заряду.
Элементарный электрический
заряд равен 1,6×10-19 Кл
Носителем элементарного положительного электрического заряда является протон.
mp = 1,67×10-27 кг.
Носителем элементарного отрицательного электрического заряда является электрон.
me = 9,11×10-31 кг.
Слайд 8
Свойства электрического заряда
Все тела в природе способны
наэлектризовываться или электризоваться, т.е. заряжаться или приобретать электрический заряд.
Всякий процесс заряжения сводится к разделению (поляризации) зарядов, когда на одном из тел или части тела возникает избыток положительного заряда, а на другом конце отрицательного.
Общее количество зарядов обоих знаков находящихся в телах не меняется. Заряды только перераспределяются в системе.
Так проявляется фундаментальный закон природы - закон сохранения электрического заряда.
Слайд 9
Закон сохранения электрического заряда:
алгебраическая сумма электрических зарядов любой
замкнутой системы остается неизменной, какие бы процессы в этой
системе не происходили.Замкнутой называют систему, не обменивающуюся зарядами с внешними телами.
Слайд 10
1.2. Закон кулона
1.2.1. Понятие точечного заряда.
Для описания взаимодействия электрических
зарядов вводится понятие точечный заряд
заряд, сосредоточенный на теле, линейные
размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует. Понятие точечного заряда, как и материальной точки, является физической абстракцией
Слайд 11
1.2.2. Эмпирическая природа открытия закона Кулона.
Силы взаимодействия неподвижных
точечных зарядов описываются законом, экспериментально установленным Ш. Кулоном (1785)
с помощью крутильных весов. Этот закон был открыт Г. Кавендишем, однако его забота оставалась неизвестной более 100 лет.
Слайд 12
Формулировка закона Кулона
Сила взаимодействия F между двумя
неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1,
Q2 и обратно пропорциональна квадрату расстояния r между ними:
Слайд 13
Векторная форма закона Кулона.
Сила F направлена по
прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и
соответствует притяжению (F < 0) в случае разноименных зарядов и отталкиванию (F > 0) в случае одноименных. Эту силу называют кулоновской.
Слайд 14
Силы кулоновского взаимодействия и III закон Ньютона.
Кулоновские
силы подчиняются третьему закону Ньютона, они равны по модулю;
направлены противоположно друг другу вдоль прямой, соединяющей точечные заряды. Силы действуют парами; являются силами одной природы; приложены к разным телам (зарядам)
Слайд 15
Электрическая постоянная
ε0=8,85×10-12 Кл2/(Н⋅м2)
ε0=8,85×10-12 Ф/м
=9×109 (Н⋅м2)/Кл2= 9×109 м/Ф
Слайд 16 Экспериментальная проверка закона Кулона на макро и микро
дистанциях.
Точность выполнения закона Кулона на больших расстояниях, вплоть
до 107 м, установлена с помощью спутников в околоземном пространстве. Считается, что закон Кулона должен соблюдаться и для больших расстояний, однако прямых экспериментов не проводилось.
Этот закон выполняется и для малых расстояний, вплоть до 10-5 м (доказано в опытах Резерфорда).
Дальнейшие эксперименты по упругому рассеянию электронов с энергией ( 109 эВ) убедительно доказали выполнимость закона Кулона на расстояниях ( 10-17 м).
Слайд 17
Физических смысл величин в законе Кулона
Из формулировки
закона Кулона
следует, что два точечных заряда по 1 Кл
каждый, расположенных в вакууме на расстоянии 1 м друг от друга, взаимодействуют с силой 9⋅109 Н.На практике пользуются дольными единицами 1 мкКл (10-6 Кл), 1 нКл, (10-9 Кл) или 1 пКл (10-12 Кл).
Слайд 18
Напряженность электростатического поля.
Электрический заряд создает электрическое поле
(на этот факт впервые указал Фарадей). Посредством этого поля
электрические заряды взаимодействуют между собой.Электрические поля, которые создаются неподвижными электрическими зарядами называются электростатическими.
В настоящее время в физике принята теория близкодействия, согласно которой взаимодействие электрических зарядов результат действия поля одного заряда на другой заряд и поля второго заряда на первый.
Взаимодействие между зарядами осуществляется посредством электрического поля, непрерывно распределенного в пространстве.
Слайд 19 Электромагнитные поля распространяются в пространстве со скоростью света.
Электромагнитное поле - особая форма материи, посредством которой осуществляются
электромагнитные взаимодействия заряженных тел, в общем случае движущихся относительно данной системы отсчета.Электрическое поле - составная часть единого электромагнитного поля.
Слайд 20 Для обнаружения и опытного исследования электростатического поля используется
пробный точечный положительный заряд — такой заряд, который не
искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле).Если в поле, создаваемом зарядом Q, поместить пробный заряд Qo, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q0
Слайд 21
Напряженность электростатического поля
в данной точке
есть физическая величина, определяемая силой, действующей на пробный единичный
положительный заряд, помещенный в эту точку поля:Единица напряженности электростатического поля в СИ ньютон на кулон (Н/Кл)
1 Н/Кл - напряженность такого поля, которое на точечный заряд 1 Кл действует силой в 1 Н
Обычно в таблицах используют размерность напряженности В/м (1 Н/Кл = 1 В/м),
Слайд 22 Отношение не зависит от Q0 и характеризует электростатическое
поле в той точке, где пробный заряд находится. Напряженность
является силовой характеристикой электростатического поля.
Слайд 23
Напряженность поля точечного заряда в вакууме
подставив в
формулу определения напряженности закон Кулона получим
Слайд 24 Направление вектора Е совпадает с направлением силы, действующей
на положительный заряд.
Если поле создается положительным зарядом, то
вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство.(отталкивание пробного положительного заряда)
Если поле создается отрицательным зарядом, то вектор Е направлен к заряду
(притяжение пробного положительного заряда)
Слайд 25
Графическое изображение электростатических полей.
Линии, касательные к которым
в каждой точке совпадают с направлением вектора поля. называются
силовые линии поля. Онм описывают напряженность поля.В этом случае их можно называть - линиями напряженности
Линиям напряженности приписывают направление, совпадающее с направлением вектора Е в рассматриваемой точке линии.
Слайд 26 Так как в каждой данной точке пространства вектор
напряженности имеет лишь одно направление, то силовые линии векторного
поля напряженности никогда не пересекаются.В случае однородного поля (вектор напряженности в любой точке постоянен по модулю и направлению) - линии напряженности параллельны вектору напряженности.
Если поле создается точечным положительным зарядом, то линии напряженности - радиальные прямые, выходящие из заряда.
Если поле создается точечным отрицательным зарядом, то линии напряженности - радиальные прямые, входящие в заряд
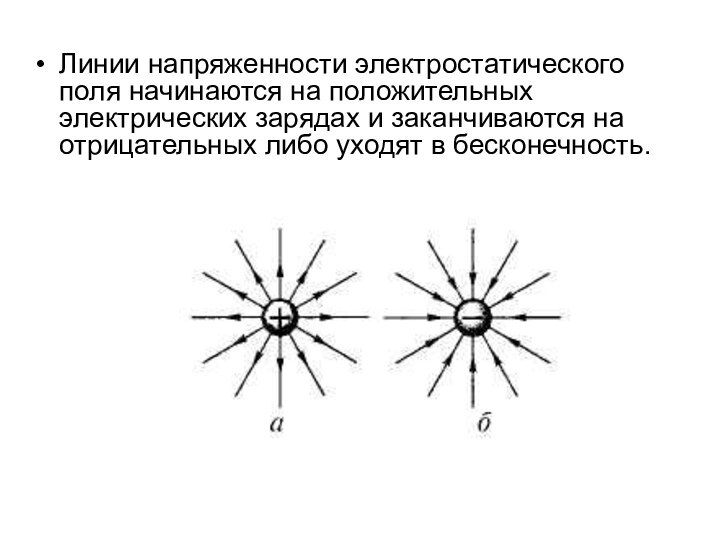
Слайд 27 Линии напряженности электростатического поля начинаются на положительных электрических
зарядах и заканчиваются на отрицательных либо уходят в бесконечность.
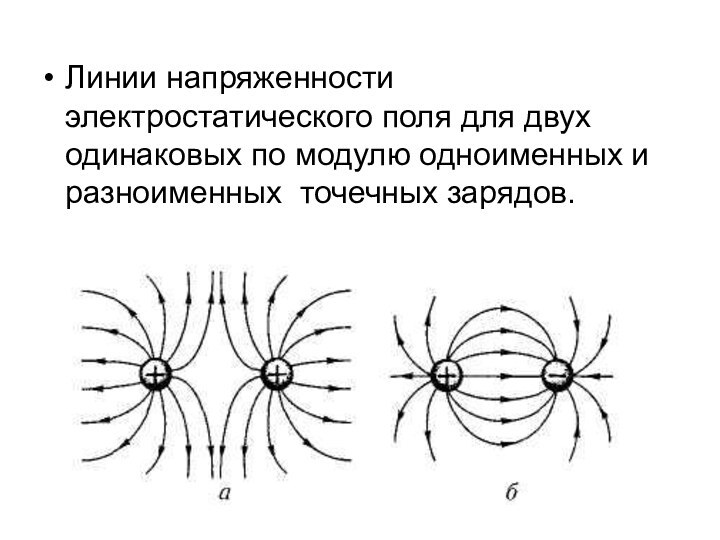
Слайд 28 Линии напряженности электростатического поля для двух одинаковых по
модулю одноименных и разноименных точечных зарядов.
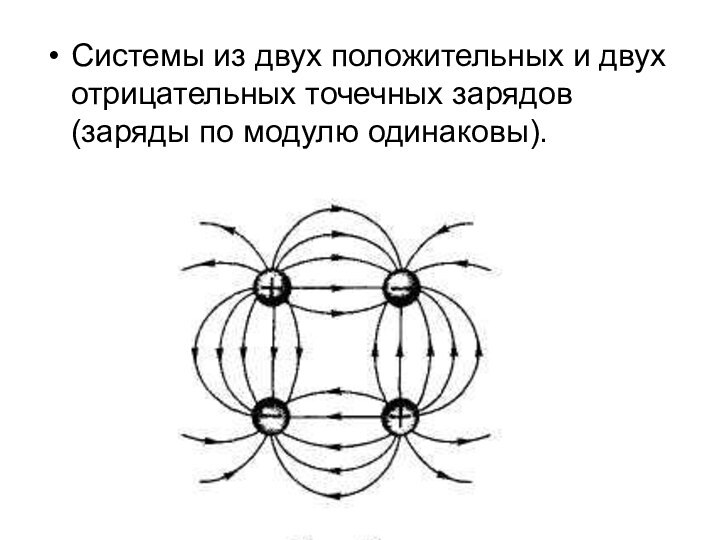
Слайд 29 Системы из двух положительных и двух отрицательных точечных
зарядов (заряды по модулю одинаковы).
Слайд 30
Принцип суперпозиции электростатических полей
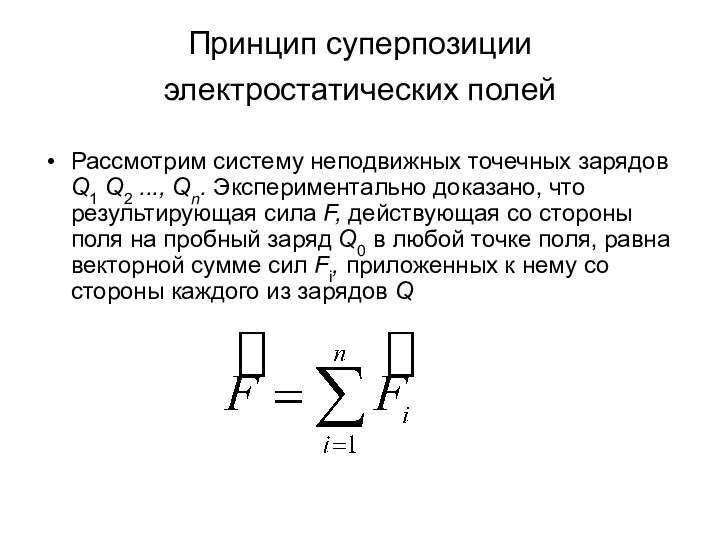
Рассмотрим систему неподвижных точечных
зарядов Q1 Q2 ..., Qn. Экспериментально доказано, что результирующая
сила F, действующая со стороны поля на пробный заряд Q0 в любой точке поля, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Q
Слайд 31
Согласно определению напряженности
получим
F = Q0E и Fi = Q0Ei
E-
напряженность результирующего поля,Ei - напряженность поля, создаваемого зарядом Qi.
Подставив эти выражения в формулу
получим:
Слайд 32
Эта формула выражает принцип суперпозиции (наложения) электростатических полей
напряженность
результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей
полей, создаваемых в данной точке каждым из зарядов в отдельности.
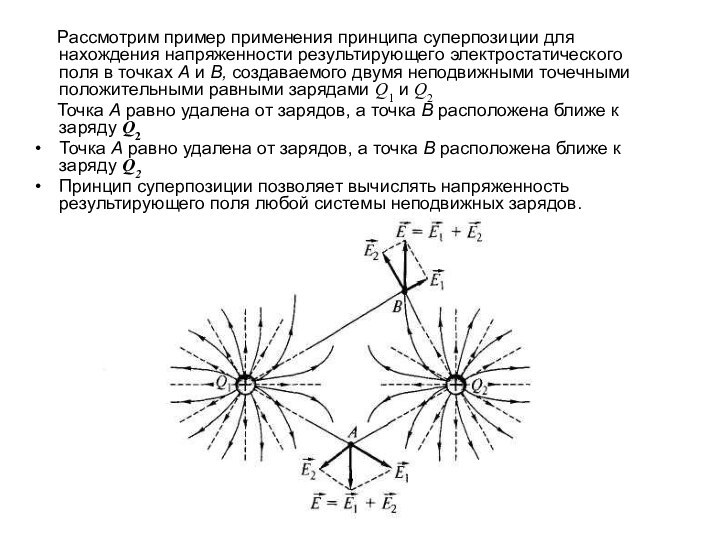
Слайд 33 Рассмотрим пример применения принципа суперпозиции
для нахождения напряженности результирующего электростатического поля в точках А
и В, создаваемого двумя неподвижными точечными положительными равными зарядами Q1 и Q2Точка А равно удалена от зарядов, а точка В расположена ближе к заряду Q2
Точка А равно удалена от зарядов, а точка В расположена ближе к заряду Q2
Принцип суперпозиции позволяет вычислять напряженность результирующего поля любой системы неподвижных зарядов.
Слайд 34 Отметим, что принцип суперпозиции является обобщением опытных данных
и, возможно, нарушается на малых расстояниях менее 10-15 м.
Принцип
суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда мысленно разделить на малые части, считая каждую из них точечным зарядом.
Слайд 35
Поле электрического диполя в вакууме
Электрический диполь —
система двух равных по модулю разноименных точечных зарядов (+Q,
—Q),расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля.
Вектор, направленный по оси диполя (прямой, проходящей через оба заряда)
от отрицательного заряда к положительному
и равный расстоянию между ними,
называют плечом диполя l .
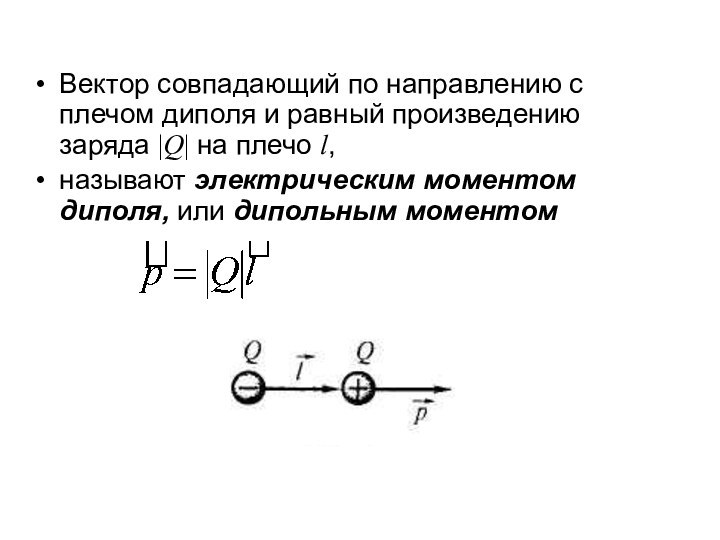
Слайд 36 Вектор совпадающий по направлению с плечом диполя и
равный произведению заряда |Q| на плечо l,
называют электрическим
моментом диполя, или дипольным моментом
Слайд 37 Применяя принцип суперпозиции электростатических полей, напряженность Е поля
диполя в произвольной точке
где Е+ и Е_ — напряженности
полей, создаваемых соответственно положительным и отрицательным зарядами.
Слайд 38
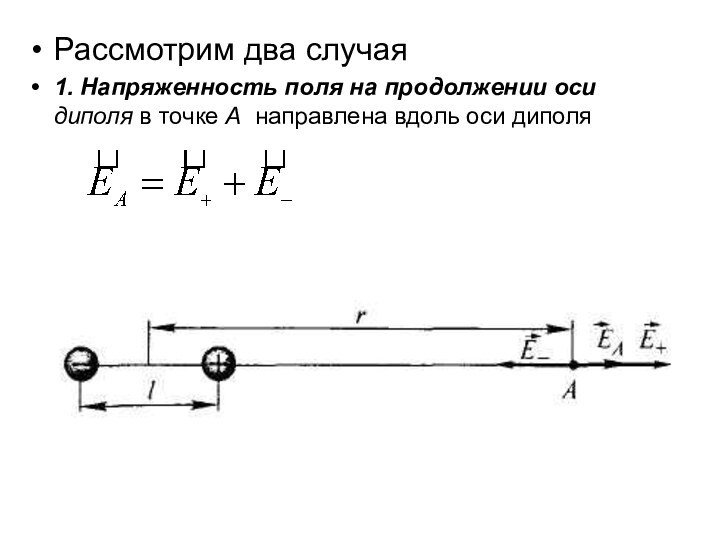
Рассмотрим два случая
1. Напряженность поля на продолжении
оси диполя в точке А направлена вдоль оси диполя
Слайд 39 Обозначив расстояние от точки А до середины оси
диполя через r, используя соотношение
получим
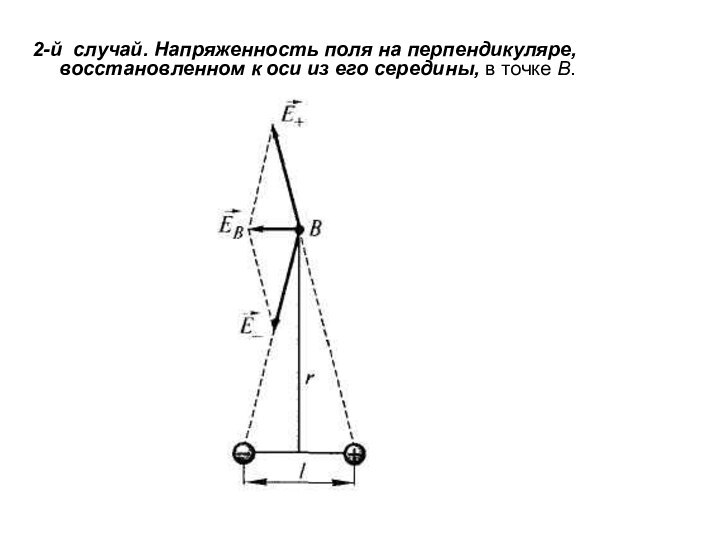
Слайд 41 2-й случай. Напряженность поля на перпендикуляре, восстановленном к
оси из его середины, в точке В.
Слайд 42
Точка В равноудалена от зарядов, поэтому
где r - расстояние от точки
В до середины плеча диполя.
Слайд 43 Из подобия равнобедренных треугольников, опирающихся на
