- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
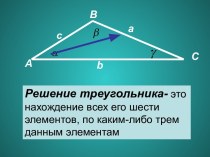
Презентация на тему ГИА 2013 Модуль Геометрия № 11
Содержание
- 2. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ: 6.Найти площадь треугольника.В С А 8 3 30⁰
- 3. ПовторениеПлощадь треугольника равна половине произведения двух сторон на синус угла между ними
- 4. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ: 31,5.Катет АС на
- 5. ПовторениеПлощадь прямоугольного треугольника равна половине произведения катетов
- 6. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ: .Найти площадь треугольникаВ А С 4
- 7. ПовторениеПлощадь треугольника равна половине произведения двух сторон
- 8. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: 13,5.АВ=3CH.Найти площадь треугольника АВСВ С А 3 H АВ=3CH=3∙3=9
- 9. ПовторениеВысота треугольника – это отрезок, проведенный из
- 10. Модуль «ГЕОМЕТРИЯ» №11Повторение (1)Ответ:1,5 .P∆ABC =6. Найти S∆ABC В С А O
- 11. ПовторениеЕсли в треугольник вписана окружность, то площадь
- 12. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: .Найти S∆ABCВ А D С 8 5
- 13. ПовторениеПлощадь параллелограмма равна произведению двух сторон на
- 14. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: 42.Диагонали ромба равны 12 и 7.Найти площадь ромба.В А D С
- 15. ПовторениеПлощадь ромба равна половине произведения его диагоналейРомб – это параллелограмм с равными сторонами
- 16. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: 73,5.ABCD – трапеция.
- 17. ПовторениеПлощадь трапеции равна произведению полусуммы оснований на высотуТрапеция – это четырехугольник, две стороны которого параллельны
- 18. Модуль «ГЕОМЕТРИЯ» №11Повторение (5)Ответ:
- 19. ПовторениеДиагонали прямоугольника равны и делятся точкой пересечения
- 20. Модуль «ГЕОМЕТРИЯ» №11Повторение (4)Ответ:
- 21. ПовторениеПлощадь трапеции равна произведению полусуммы оснований на
- 22. Модуль «ГЕОМЕТРИЯ» №11Повторение (4)Ответ: 168.P∆ABC =98.
- 23. ПовторениеПериметр треугольника – это сумма длин сторон
- 24. Модуль «ГЕОМЕТРИЯ» №11Повторение (4)Ответ: 9.В прямоугольном треугольнике
- 25. ПовторениеЕсли высота треугольника является и медианой, то
- 26. Модуль «ГЕОМЕТРИЯ» №11Повторение (4)Ответ:
- 27. ПовторениеКосинус острого угла прямоугольного треугольника равен отношению
- 28. Модуль «ГЕОМЕТРИЯ» №11Повторение (4)Ответ: 90.Четырехугольник АВСD описан
- 29. ПовторениеЕсли в четырехугольник можно вписать окружность, то
- 30. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ:
- 31. ПовторениеДиагонали ромба перпендикулярны и делят углы ромба
- 32. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: 12.Найти площадь параллелограммаВ
- 33. ПовторениеТреугольник, в котором стороны равны 3,4,5 называется
- 34. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: 192π .Дуга сектора
- 35. ПовторениеДлина окружности равна удвоенному произведению числа π на радиус окружностиПлощадь кругового сектора вычисляется по формуле
- 36. Модуль «ГЕОМЕТРИЯ» №11Повторение (2)Ответ: .Найти площадь кольца3 5 ⇒
- 37. ПовторениеПлощадь круга равна произведению числа π на
- 38. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ:
- 39. ПовторениеСторона правильного треугольника, в который вписана окружность,
- 40. Модуль «ГЕОМЕТРИЯ» №11Повторение (3)Ответ:
- 41. ПовторениеСторона правильного четырехугольника, в который вписана окружность,
- 42. Скачать презентацию
- 43. Похожие презентации







































Слайд 3
Повторение
Площадь треугольника равна половине произведения двух сторон на
синус угла между ними
Слайд 4
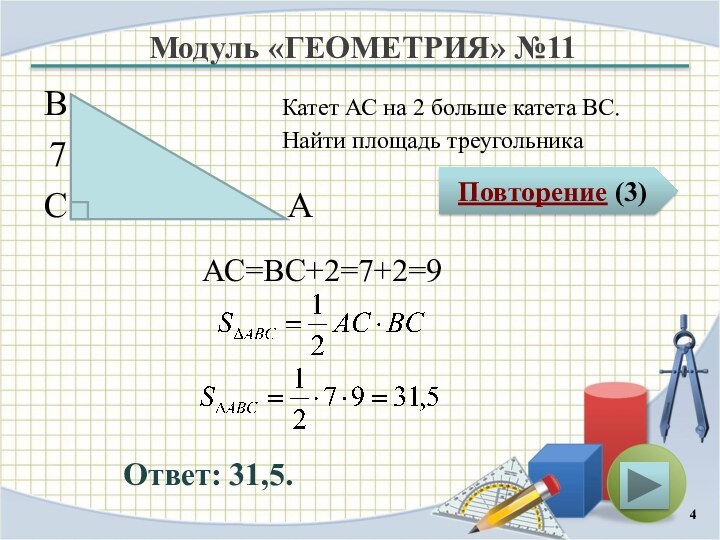
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: 31,5.
Катет АС на 2
больше катета ВС.
Найти площадь треугольника
В
С
А
7
АС=ВС+2=7+2=9
Слайд 7
Повторение
Площадь треугольника равна половине произведения двух сторон на
синус угла между ними
Сумма квадратов синуса и косинуса одного
и того же угла равна единице
Слайд 8
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 13,5.
АВ=3CH.
Найти площадь треугольника АВС
В
С
А
3
H
АВ=3CH=3∙3=9
Слайд 9
Повторение
Высота треугольника – это отрезок, проведенный из вершины
к противоположной стороне под прямым углом
Площадь треугольника равна половине
произведения основания на высоту
Слайд 11
Повторение
Если в треугольник вписана окружность, то площадь треугольника
равна произведению полупериметра треугольника на радиус вписанной окружности
Вписанной в
треугольник окружностью называется окружность, которая касается всех сторон треугольника
Слайд 13
Повторение
Площадь параллелограмма равна произведению двух сторон на синус
угла между ними
Сумма квадратов синуса и косинуса одного и
того же угла равна единице
Слайд 14
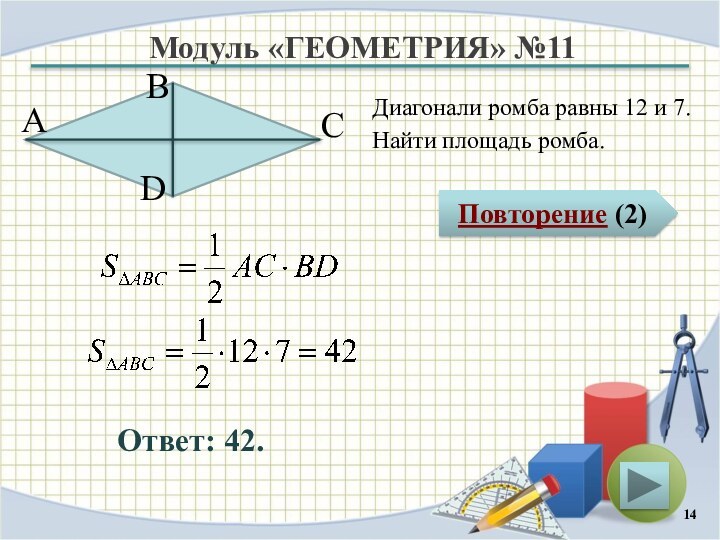
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 42.
Диагонали ромба равны 12
и 7.
Найти площадь ромба.
В
А
D
С
Слайд 15
Повторение
Площадь ромба равна половине произведения его диагоналей
Ромб –
это параллелограмм с равными сторонами
Слайд 16
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 73,5.
ABCD – трапеция. ВС
в 2 раза меньше AD. Найти площадь трапеции
В
А
D
С
14
H
ВС=14:2=7
BC=DH=7
Слайд 17
Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Трапеция
– это четырехугольник, две стороны которого параллельны
Слайд 18
Модуль «ГЕОМЕТРИЯ» №11
Повторение (5)
Ответ:
.
АС=10.
Найти площадь прямоугольника
В
А
D
С
60⁰
О
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰
⇒
АВ=5
По теореме Пифагора в ∆АВD
Слайд 19
Повторение
Диагонали прямоугольника равны и делятся точкой пересечения пополам
В
равнобедренном треугольнике углы при основании равны
Если угол разбит на
части, то его градусная мера равна сумме его частейВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению соседних сторон
Слайд 20
Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ:
.
ABCD – равнобедренная трапеция MK=8, боковая сторона равна
5.Найти площадь трапеции.
В
А
D
С
8
135⁰
H
К
М
⇒
По теореме Пифагора в ∆АВH, где AH=BH=х
∠АВH=90⁰=135⁰-90⁰=45⁰
⇒
∠ВАH= ∠АВC=45⁰
⇒
Слайд 21
Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Средняя
линия трапеции равна полусумме оснований
Если в прямоугольном треугольнике острый
угол равен 45⁰, то и другой острый угол равен 45⁰ В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 22
Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 168.
P∆ABC =98.
Найти S∆ABC
В
С
А
25
H
АВ=P∆ABC –2ВС=98–2∙25=48
Т.к. ∆АВС равнобедренный, то АH=HB=48:2=24
По теореме Пифагора в ∆АСH
Слайд 23
Повторение
Периметр треугольника – это сумма длин сторон треугольника
Высота
в равнобедренном треугольнике, проведенная к основанию является медианой
В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетовПлощадь треугольника равна половине произведения основания на высоту
Слайд 24
Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 9.
В прямоугольном треугольнике высота,
проведенная из вершины прямого угла, равна медиане, проведенной из
того же угла, АВ=6. Найти S∆ABCВ
С
А
H
Если высота треугольника равна медиане, то ∆АВС – равнобедренный с основанием АВ
⇒
∠А=∠В=45⁰
∆HBC прямоугольный и равнобедренный, так как∠В=45⁰
⇒
CH=HВ=AB:2=3
Слайд 25
Повторение
Если высота треугольника является и медианой, то такой
треугольник равнобедренный
Если прямоугольный треугольник равнобедренный, то его острые углы
равны 45⁰В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту
Слайд 26
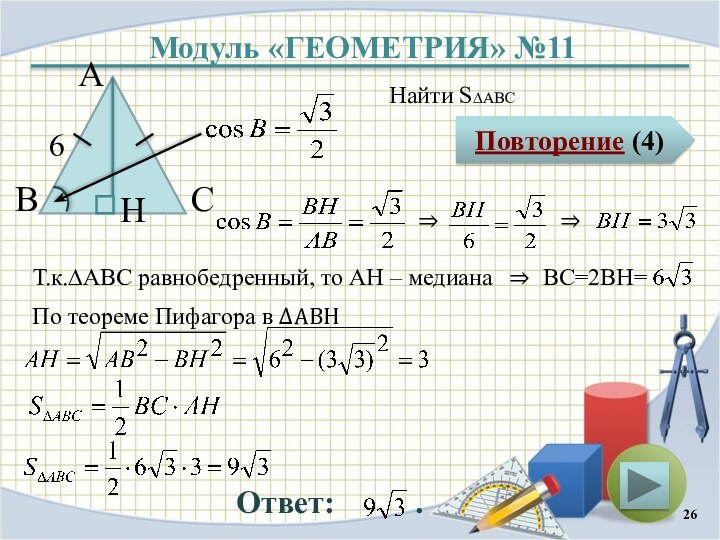
Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ:
.
Найти S∆ABC
В
С
А
6
H
⇒
⇒
Т.к.∆АBC равнобедренный, то AH – медиана ⇒
BC=2BH=
По теореме Пифагора в ∆АВH
Слайд 27
Повторение
Косинус острого угла прямоугольного треугольника равен отношению прилежащего
катета к гипотенузе
Высота прямоугольного треугольника, проведенная к основанию, является
медианойВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту
Слайд 28
Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 90.
Четырехугольник АВСD описан около
четырехугольника, радиуса 4,5.
Найти S∆ABCD.В
А
D
С
5
15
4,5
О
Соединим центр окружности с вершинами четырехугольника
Получим треугольники, высоты которых равны радиусу окружности
AB+DC=AD+BC
⇒
S∆AОB +S∆BOC =S∆COD +S∆AOD
SABCD =2(S∆AОB +S∆BOC)
⇒
Слайд 29
Повторение
Если в четырехугольник можно вписать окружность, то суммы
противоположных сторон четырехугольника равны
Если фигура разбита на части, то
площадь фигуры равна сумме площадей ее частейРадиус, проведенный в точку касания перпендикулярен касательной
Площадь треугольника равна половине произведения основания на высоту
Слайд 30
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ:
.
ABCD – ромб.
Найти площадь ромба.
В
А
D
С
60⁰
18
O
В ∆АОB ∠ВОА=30⁰
⇒
По теореме Пифагора в ∆АВО
BD=2BO=18,
Слайд 31
Повторение
Диагонали ромба перпендикулярны и делят углы ромба пополам
В
прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь ромба
равна половине произведения его диагоналей
Слайд 32
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 12.
Найти площадь параллелограмма
В
А
D
С
5
4
3
В
А
D
С
5
4
3
Так как ∆АВС – прямоугольный, то параллелограмм трансформируется в прямоугольник
Слайд 33
Повторение
Треугольник, в котором стороны равны 3,4,5 называется Пифагоровым
(т.е. треугольник является прямоугольным)
Площадь прямоугольника равна произведению его измерений
Слайд 34
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 192π .
Дуга сектора равна
8π. Найти площадь сектора.
30⁰
O
А
В
Сокр.=360⁰:30⁰∙ 8π=96π
Сокр.=2πr
⇒
Слайд 35
Повторение
Длина окружности равна удвоенному произведению числа π на
радиус окружности
Площадь кругового сектора
вычисляется по формуле
Слайд 37
Повторение
Площадь круга равна произведению числа π на квадрат
радиуса круга
Если фигура разделена на части, то его площадь
равна сумме площадей его частей
Слайд 38
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ:
.
Найти площадь круга, вписанного в равносторонний треугольник
В
С
А
⇒
⇒
Слайд 39
Повторение
Сторона правильного треугольника, в который вписана окружность, равна
Радиусы вписанной и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна произведению числа π на квадрат радиуса круга
Слайд 40
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: .
Найти
площадь круга, вписанного в квадрат со стороной 18.
18
⇒
⇒
Слайд 41
Повторение
Сторона правильного четырехугольника, в который вписана окружность, равна
Радиусы вписанной и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна произведению числа π на квадрат радиуса круга