- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по дисциплине Элементы математической логики
Содержание
- 2. Вопросы для освоения1? Понятие таблицы истинности. Таблицы истинности для всех логических операций.2? Приоритет выполнения логических операций.
- 3. « Стремление к истине — единственное занятие,
- 4. . Опр. Таблица истинности – это
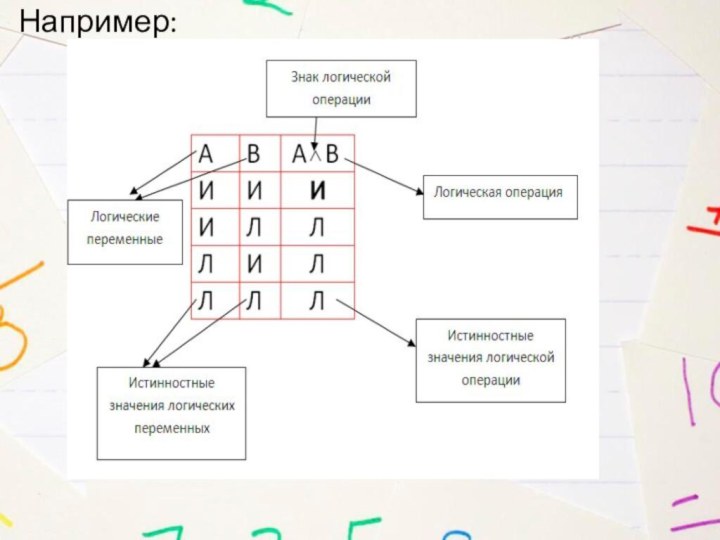
- 5. Например:
- 6. Приведем таблицы истинности логических операций для
- 7. 2)Конъюнкцияэто логическая операция А٨В, которая принимает истинное
- 8. 3)Дизъюнкция -
- 9. 4) Импликация- это логическая операция А →В,
- 10. 5) Эквиваленция - это логическая операция А
- 11. 6)Штрих Шеффера - это логическая операция А
- 12. 7) Стрелка Пирса - это логическая
- 13. 8) Сумма по модулю 2- это логическая
- 14. Таблица истинности для 3х аргументов Количество
- 15. При наличии нескольких логических операций в выражении,
- 16. Алгоритм построения таблицы истинности Подсчитать n- количество
- 17. Пример работы по алгоритму:Задание: Построить таблицу истинности
- 18. 6. Выписать наборы входных переменных7. Провести заполнение
- 19. Скачать презентацию
- 20. Похожие презентации
Вопросы для освоения1? Понятие таблицы истинности. Таблицы истинности для всех логических операций.2? Приоритет выполнения логических операций.

















Слайд 2
Вопросы для освоения
1? Понятие таблицы истинности.
Таблицы истинности
для всех логических операций.
Слайд 3 « Стремление к истине — единственное занятие, достойное
героя. »
Джордано Бруно
итальянский монах-доминиканец,
философ и поэт,
1548 г.-
1600 г.
Слайд 4
.
Опр. Таблица истинности – это табличное представление логической
операции, в которой перечислены все возможные сочетания значений истинности
входных операндов (логических переменных). Вместе со значением истинности результата логических операций для каждого из этих сочетаний.Таблицы истинности
Слайд 6 Приведем таблицы истинности логических операций для 1 и
2 логических переменных: 1) Отрицание - это логическая операция, которая
принимает истинное значение, когда значение логической переменной ложно.
Таблица истинности имеет вид:
Где А - логическая переменная,
Ā – отрицание
логической переменной, (не А).
Слайд 7
2)Конъюнкция
это логическая операция А٨В, которая принимает истинное значение,
когда обе А и В (все) логические переменные принимают
истинное значение.Таблица истинности имеет вид:
Где А и В – логические
переменные,
А٨В – логическая операция
конъюнкция.
Слайд 8
3)Дизъюнкция
- логическая операция
А٧В ложна тогда и только тогда, когда значения обеих
логических переменных А и В – ложны.Таблица истинности имеет вид:
Где А и В – логические
переменные,
А٧В –логическая операция
дизъюнкция.
Слайд 9
4) Импликация
- это логическая операция А →В, которая
принимает ложное значение, тогда и только тогда, когда первая
логическая переменная А принимает истинное значение, а вторая переменная В принимают ложное значение.Таблица истинности имеет вид:
Где А и В –логические
переменные,
А →В - импликация
Слайд 10
5) Эквиваленция
- это логическая операция А
↔В, которая принимает истинное значение, тогда и только тогда,
когда истинностные значения логических переменных совпадают.Таблица истинности имеет вид:
А и В – логические
переменые,
А ↔В – логическая
операция
эквиваленция
Слайд 11
6)Штрих Шеффера
- это логическая операция А
/В, которая принимает ложное значение, тогда и только тогда,
когда обе логические переменные принимают истинные значения.Таблица истинности имеет вид:
Где А и В – логические
переменные,
А /В – логическая
операция
штрих Шеффера
Слайд 12
7) Стрелка Пирса
- это логическая операция А↓В,
которая принимает истинное значение, тогда и только тогда, когда
обе логические переменные принимают значения «ложь».Таблица истинности имеет вид:
Где А и В – логические
переменные,
А ↓В – логическая
операция
стрелка Пирса
Слайд 13
8) Сумма по модулю 2
- это логическая операция
А В, которая принимает ложное значение, тогда и
только тогда, когда обе логические переменные принимают истинные значения.Таблица истинности имеет вид:
Где А и В – логические
переменные,
А В – логическая
операция
сумма по модулю 2
Слайд 14
Таблица истинности для 3х аргументов
Количество сочетаний для
логических операций рассчитывается по формуле 2N, где N- количество
аргументов. Для трех аргументов (логических переменных) 23=8. Следовательно, 8 наборов истинностных значений (число строк) будет в таблице истинности.Где А,В,С – логические
переменные.
Слайд 15 При наличии нескольких логических операций в выражении, приоритет
в решении будет следующий:
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
Штрих
Шеффера, стрелка Пирса, сумма по модулю 2.Приоритет выполнения логических операций
Слайд 16
Алгоритм построения таблицы истинности
Подсчитать n- количество переменных в
формуле.
Определить число строк в таблице m=2n.
Подсчитать количество логических операций
в формуле.Установить последовательность выполнения логических операций с учетом скобок и приоритетов.
Определить количество столбцов в таблице: число переменных плюс число операций.
Выписать наборы входных переменных с учетом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2n-1.
Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии установленной в п.4 последовательности.
Слайд 17
Пример работы по алгоритму:
Задание: Построить таблицу истинности по
следующей формуле А→ Ā٨В.
Решение:
Количество переменных в формуле
А и
В =2.2. Число строк в таблице истинности
m=4.
3. Количество логических операций в формуле-
отриц., импликация, конъюнкция – 3
4. Последовательность
-1.отрицание,2.конъюнкция.,3.импликация
5. Количество столбцов в таблице: число переменных плюс число операций
= 2+3 =5столбцов.