Презентация на тему к уроку информатики Формы мышления. Алгебра высказываний.

логическое высказывание, логические операции;
способствовать формированию умений переводить высказывания

на язык алгебры логики, определять истинность (ложность) высказываний;
способствовать развитию познавательного интереса;
воспитывать культуру общения, взаимопомощь учащихся.

и способах мышления.
Законы логики отражают в сознании человека свойства,

связи и отношения объектов окружающего мира.

существенные признаки объекта.
Две стороны понятия:
Содержание (Совокупность существенных свойств, которые

мыслятся в данном понятии)
Объем (Совокупность предметов, которые мыслятся в данном понятии)

Приведите пример понятия, раскройте его содержание и определите объём.

?

понятия некоторого нового с более широким объемом
Ограничение

Переход от понятия с большим объемом к понятию с меньшим объемом
Определение Раскрытие содержания понятия
Деление Распределение объема понятия на классы с точки зрения некоторого признака
Классификация Многоступенчатое, разветвленное деление.

что-либо утверждается или отрицается о свойствах реальных предметов и

отношениях между ними.
Логическое высказывание— это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.

Все рыбы дышат жабрами

Волга впадает в Каспийское море

если никакая его часть сама не является высказыванием.

      

Аристотель - основоположник логики

Сегодня холодно и идет дождь

Высказывание, состоящее
из простых высказываний,
называется составным (сложным).

одного или нескольких истинных суждений, называемых посылками, по определенным

правилам получают суждение-заключение.

раздел математической логики, изучающий строение (форму, структуру) сложных логических

высказываний и способы установления их истинности с помощью алгебраических методов .

Джордж Буль
считается отцом математической логики. Его именем назван раздел математической логики - булева алгебра.

Чтобы подключиться к Интернету с домашнего компьютера, необходим модем

.
Если высказывание А истинное, то будем писать
«А = 1»
и говорить «А – истинно».
Если высказывание А ложное,
то будем писать «А = 0»
и говорить «А – ложно».

высказывания из данных высказываний, при котором значение истинности сложного

высказывания полностью определяется значениями истинности исходных высказываний.
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция

в естественном языке соответствует союзу и;
обозначение: &;
в

языках программирования обозначение: and;
иное название: логическое умножение.
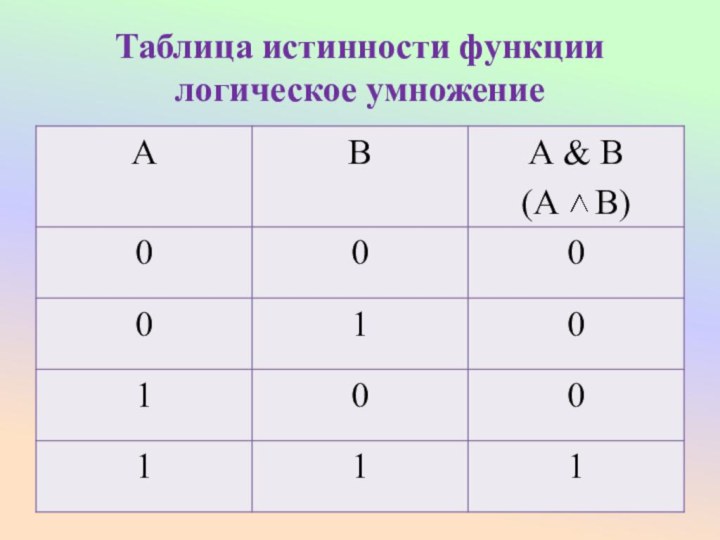
      Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

естественном языке соответствует союзу или;
обозначение:

;
в языках программирования обозначение: or;
иное название: логическое сложение.
       Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

(лат. inversio — переворачиваю):
в естественном языке

соответствует словам "Неверно, что... " и частице не;

обозначение: ;
в языках программирования обозначение: not;
иное название: отрицание.
        Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

высказываниями:
1)      Какого цвета этот дом?
2)      Число Х

не превосходит единицы.
3)      4Х+3
4)      Посмотрите в окно.
5)      Пейте томатный сок!
6)      Вы были в театре?
7)      Сумма числа 5 и Х равна 10.

а какие ложными высказываниями?
1) Город Париж — столица Франции.

2) Число 2 является делителем числа 7.
3) 3 + 5 = 2 ´ 4.
4) 2 + 6 > 10.
5) Сканер — это устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.
6) II + VI > VIII.
7) Сумма чисел 2 и 6 больше числа 8.
8) Мышка — устройство ввода информации.

высказываний из:
1)      биологии;
2)      географии;
3)      информатики;
4)     

истории;
5)      литературы;
6)      математики;
7)      русского языка.

составное число.
2) Натуральные числа, оканчивающиеся цифрой 0, являются простыми

числами.
3) Неверно, что число 3 не является делителем числа 198.
4) Неверно, что любое число, оканчивающееся цифрой 4, делится на 4.
5) Некоторые млекопитающие не живут на суше.  

отрицаниями друг друга:
1)   “1999 < 2000”, “1999

> 2000”, “1999 <= 2000”;

2)   “Луна — спутник Земли”,
“Неверно, что Луна спутник Земли”,
“Неверно, что Луна не является спутником Земли”;

3)   “Прямая m не параллельна прямой с”,
“Прямая m перпендикулярна прямой с”,
“Прямые m и с не пересекаются” (считаем, что прямые m и с лежат в одной плоскости);

4)  “Мишень поражена первым выстрелом”,
“Мишень поражена не первым выстрелом”,
“Неверно, что мишень поражена не первым выстрелом”.

есть орудие доказательства»

А. Пуанкаре