- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к року Технологии информационного моделирования.
Содержание
- 2. ПЛАН:Моделирование зависимостей между величинамиМодели статистического прогнозированияМоделирование корреляционных зависимостейМодели оптимального планирования
- 3. Применение математического моделированияПримеры зависимостей:время падения тела на
- 4. Методы представления зависимостейВеличина – количественная характеристика исследуемого
- 5. Виды зависимостейФункциональной зависимостью называется связь между двумя величинами,
- 6. Виды зависимостейИная зависимость носит более сложный характер,
- 7. Математические моделиМатематические модели — это совокупность количественных
- 8. Табличные и графические моделиЭкспериментальным путем проверим закон
- 9. Динамические моделиИнформационные модели, которые описывают развитие систем
- 10. Самое основноеВеличина – количественная характеристика исследуемого объекта.Характеристики
- 11. Статистика- наука о сборе, измерении и анализе
- 12. Сведения о средней концентрации угарного газа в
- 13. 2 варианта построения графической зависимости по экспериментальным
- 14. Два этапа получения регрессионной модели 1) подбор
- 15. Графики функций, построенные по МНК, - трендыR2 – коэффициент детерминированности (от 0 до 1)
- 16. Алгоритм построения регрессионной модели по МНК
- 17. Построение регрессионной модели по МНК с помощью MS Excel 2007 (линейный тренд)
- 18. Прогнозирование по регрессивной модели:Восстановление значений – прогноз
- 19. Корреляционная зависимость — зависимость между величинами, каждая из которых подвергается не контролируемому полностью разбросу.
- 20. Корреляционный анализ — Раздел математической статистики,
- 21. Какие задачи решает корреляционный анализ?Определить, оказывает ли
- 23. Коэффициент корреляции (ρ) — количественная мера
- 24. Как вычислить коэффициент корреляции?В MS Excel для
- 25. Опт. планированиеЭто определение значений плановых показателей с учетом ограниченности ресурсов при условии достижения заданной цели
- 26. ЗАДАЧАШкольный кондитерский цех готовит пирожки и пирожные.
- 27. Математическая модельX – пирожковУ- пирожныхДлительность рабочего дня
- 28. Математическая модель (x+4y)t
- 29. Стратегическая цель Требуется найти значения х и
- 30. Скачать презентацию
- 31. Похожие презентации




























Слайд 2
ПЛАН:
Моделирование зависимостей между величинами
Модели статистического прогнозирования
Моделирование корреляционных зависимостей
Модели
оптимального планирования
Слайд 3
Применение математического моделирования
Примеры зависимостей:
время падения тела на землю
зависит от его первоначальной высоты;
давление газа в баллоне зависит
от его температуры;уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе.
Применение математического моделирования постоянно требует учета зависимостей одних величин от других.
Реализация математической модели требует владения приемами представления зависимостей между величинами.
Слайд 4
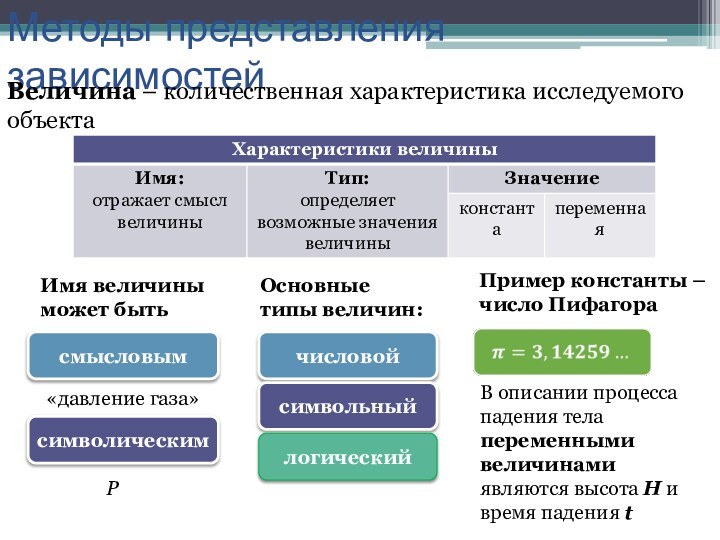
Методы представления зависимостей
Величина – количественная характеристика исследуемого объекта
Имя
величины может быть
символическим
«давление газа»
Р
Основные типы величин:
числовой
символьный
логический
Пример константы – число
Пифагора В описании процесса падения тела переменными величинами являются высота H и время падения t
смысловым
Слайд 5
Виды зависимостей
Функциональной зависимостью называется связь между двумя величинами, при
которой изменение одной из них вызывает изменение другой.
Зависимость между
величинами является полностью определенной.Пример 1: t (c) – время падения; H (m) – высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха; ускорение свободного падения g (м/с2) будем считать константой.
Пример 2: P (н/м2) – давление газа (в единицах системы СИ давление измеряется в ньютонах на квадратный метр); t °C – температура газа. Давление при нуле градусов P0 будем считать константой для данного газа.
Слайд 6
Виды зависимостей
Иная зависимость носит более сложный характер, одна
и та же величина может принять разные значения, поскольку
на нее могут оказывать влияния и другие показатели.Зависимость между величинами является полностью определенной.
Пример 3: Загрязненность воздуха характеризуется концентрацией примесей – С (мг/м3). Единица измерения – массы примесей, содержится в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будет характеризовать числом хронических больных астмой, приходящихся на 1000 жителей данного города P (бол./тыс.)
Слайд 7
Математические модели
Математические модели — это совокупность количественных характеристик
некоторого объекта (процесса) и связей между ними, представленных на
языке математики.Математические модели отражают физические законы и представляются в виде формул:
В сложных задачах математические модели представляют в виде уравнений или систем уравнений.
Корневая зависимость (время пропорционально квадратному корню высоты)
Линейная зависимость
Слайд 8
Табличные и графические модели
Экспериментальным путем проверим закон свободного
падения тела
Эксперимент: стальной шарик сброшен с 6-метровой, 9-метровой
высоты и т.д. (через 3 метра), замеряя высоту начального положения шарика и время падения Результат эксперимента представлен в таблице и графике
Табличное и графическое представление зависимости времени падения тела от высоты
Слайд 9
Динамические модели
Информационные модели, которые описывают развитие систем во
времени, имеют специальное название: динамические модели.
В физике это движение
тел, в биологии – развитие организмов или популяций животных, в химии – протекание химических реакций.
Слайд 10
Самое основное
Величина – количественная характеристика исследуемого объекта.
Характеристики величины:
Имя
– отражает смысл величины
Тип – определяет возможные значения величин
Значение:
постоянная величина (константа) или переменнаяФункциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой.
Существует три способа моделирования величин: функциональный (формула), табличный и графический
Формула более универсальна; имея формулу, можно легко создать таблицу и построить график.
Описание развития систем во времени – динамическая модель.
Слайд 11 Статистика- наука о сборе, измерении и анализе массовых
количественных данных
медицинская статистика
математический аппарат - экономическая статистика математическая статистика
социальная статистика …
Зависимости устанавливается экспериментальным путем:
сбор данных
анализ
обощение
Слайд 12 Сведения о средней концентрации угарного газа в атмосфере
C и о заболеваемости астмой (число хронических больных на
1000 жителей P.
Слайд 13
2 варианта построения графической зависимости по экспериментальным данным
Основные
требования к искомой функции:
- она должна быть достаточно простой
для использования ее в дальнейших вычислениях;график функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек о графика были минимальны и равномерны.
Полученная таким образом функция называется в статистике регрессионной моделью.
Слайд 14
Два этапа получения регрессионной модели
1) подбор вида
функции:
y = ax + b - линейная функция;
y =
ax2 + bx + c - квадратичная функция (полиномиальная);y=a ln(x) +b - логарифмическая функция;
y = aebx- экспоненциальная функция;
y = axb - степенная функция.
вычисление параметров функции:
метод наименьших квадратов - сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции должна быть минимальной.
Слайд 15
Графики функций, построенные по МНК, - тренды
R2 –
коэффициент детерминированности (от 0 до 1)
Слайд 16 Алгоритм построения регрессионной модели по МНК с помощью
MS Excel (линейный тренд)
Ввести табличные данные зависимости заболеваемости P
от концентрации угарного газа С .Построить точечную диаграмму. (В качестве подписи к оси OX выбрать название тренда - «Линейный», остальные надписи и легенду можно игнорировать).
Щелкнуть мышью по полю диаграммы; выполнить команду Диаграмма – Добавить линию тренда;
В открывшемся окне на вкладке Тип выбрать Линейный тренд;
Перейти на вкладку Параметры и установит галочки на флажках показывать уравнения на диаграмме и поместить на диаграмме величину достоверности ампроксикации R^2
щелкнуть OK.
Слайд 18
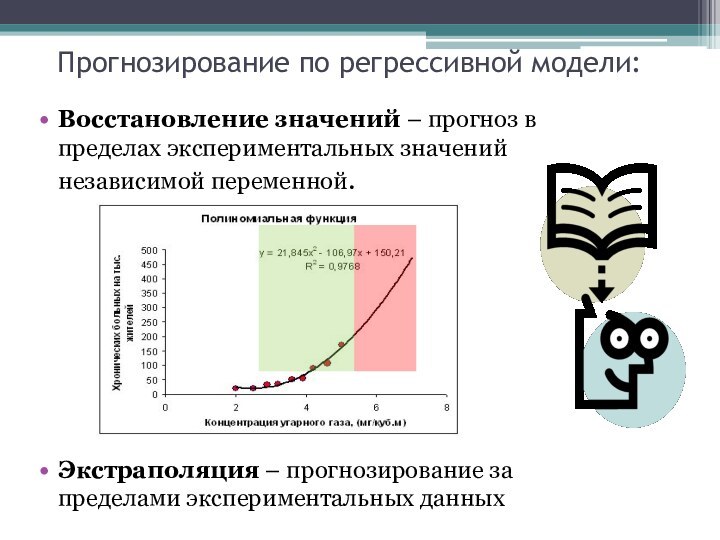
Прогнозирование по регрессивной модели:
Восстановление значений – прогноз в
пределах экспериментальных значений независимой переменной.
Экстраполяция – прогнозирование за пределами
экспериментальных данных
Слайд 19
Корреляционная зависимость
— зависимость между величинами, каждая из
которых подвергается не контролируемому полностью разбросу.
Слайд 20
Корреляционный анализ —
Раздел математической статистики, который
исследует корреляционные зависимости.
Изучает усреднённый закон поведения каждой
из величин в зависимости от значений другой величины, а также меру такой зависимости.
Слайд 21
Какие задачи решает корреляционный анализ?
Определить, оказывает ли один
фактор существенное влияние на другой фактор;
Из нескольких факторов выбрать
наиболее существенный.
Слайд 23
Коэффициент корреляции (ρ) —
количественная мера корреляции
двух величин.
- 1 ≤ ρ ≥ + 1;
если lρ
l≈ 1, то корреляция сильная;если lρ l≈ 0, то корреляция слабая;
значение ρ легко найти с помощью Excel.
Слайд 24
Как вычислить коэффициент корреляции?
В MS Excel для определения
коэффициента корреляции используется функция КОРРЕЛ из группы статистических функций.
Слайд 25
Опт. планирование
Это определение значений плановых показателей с учетом
ограниченности ресурсов при условии достижения заданной цели
Слайд 26
ЗАДАЧА
Школьный кондитерский цех готовит пирожки и пирожные. В
силу ограниченности условий можно приготовить не более 700 штук
изделий. Рабочий день длится 8 часов. За день можно произвести не более 250 пирожных, пирожков – 1000 (по отдельности).Стоимость пирожного вдвое выше стоимости пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку.
Слайд 27
Математическая модель
X – пирожков
У- пирожных
Длительность рабочего дня –
8 часов
Склад – на 700 мест
t - время на
1 пирожок4t – на 1 пирожное
tx+4ty = (x+4y)t
(x+4y)t <=8*60
(x+4y)t <=480
480/1000 = 0,48 мин – на 1 пирожок
Слайд 29
Стратегическая цель
Требуется найти значения х и у,
удовлетворяющих системе неравенств и придающих максимальное значение целевой функции
Получение
максимальной выручки!r- цена 1 пирожка
2r- цена 1 пирожного
rx +2ry = r(x+2y) – целевая функция
r=const, x+2y = max





























