нулей и единиц, которыми закодирована различная информация (числовая, текстовая,
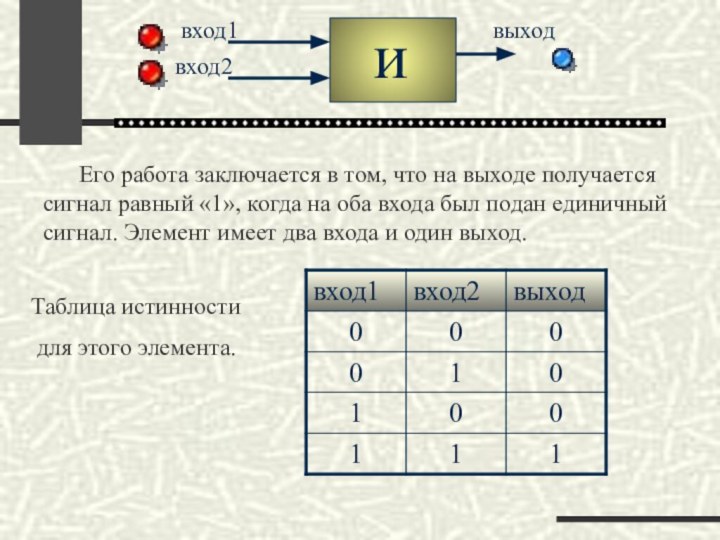
графическая, звуковая), и пересылки этой информации. Такую обработку производит арифметико- логическое устройство, являющееся частью процессора. Состоит оно из логических элементов. Логические элементы- это электронные схемы, реализующие логические операции. Эти элементы могут иметь один или несколько входов и один выход, через которые проходят электрические сигналы. Эти сигналы принято обозначать цифрами 1 и 0.
Логические элементы