Презентация на тему Системы счисления

шестнадцатеричная системы
счисления
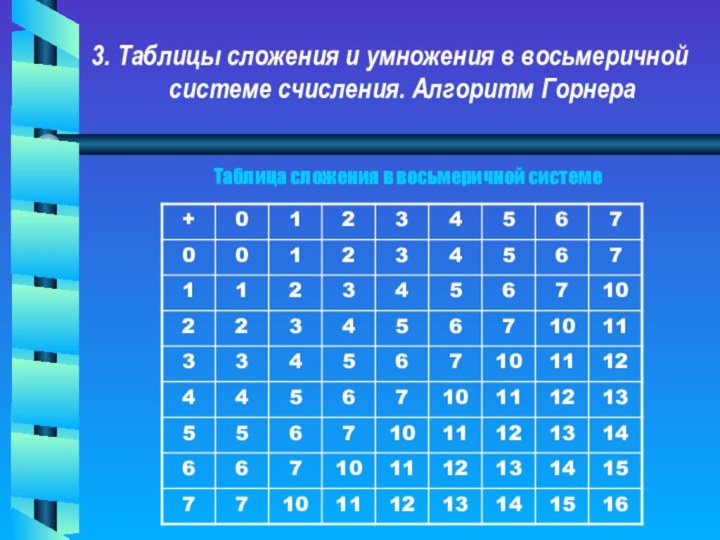
3. Таблицы сложения и

умножения в восьмеричной
системе счисления. Алгоритм Горнера

«Системы счисления»

Тема :

- основные понятия
- двоичная система счисления
- восьмеричная и шестнадцатеричная
системы счисления
- алгоритм Горнера

записи чисел цифровыми знаками или символами.

Все системы счисления можно

разделить на два класса: позиционные и непозиционные.

1. Системы счисления. Двоичная система счисления

величина числа определяется значениями входящих в него цифр и

их относительным положением в числе.
ПРИМЕР: 10-я и др.
Непозиционная система счисления – значение знака не зависит от того места, которое он занимает в числе.
В этой системе используется 7 знаков ( I, V, X, L, C, D, M ) , которые соответствуют следующим величинам:
I(1) V(5) X(10) L(50) C(100) D(500) M(1000)
ПРИМЕР: III (три), LIX (пятьдесят девять).

информатике определяется тем, что внутреннее представление любой информации в

компьютере является двоичным, т.е. описываемым набором только из двух знаков (0 и 1).

счисления, надо число делить на 2 ( в остатке

только 0 и 1 ).
Число 2510
25/2=12 (1)
12/2=6 (0)
6/2=3 (0)
3/2=1 (1)
1/2=0 (1)
Ответ: (25)10 = (11001)2

4 3 2 1 0
= 1 • 24 + 1 • 23 + 0 • 22 + 0 • 21 + 1 • 20 =
= 16 + 8 + 1 = (25)10

у которого «0» целых) надо умножить её на 2.
Число

0,73 10
0,73 • 2 = 1,46 ( целая часть 1 )
0,46 • 2 = 0,92 ( целая часть 0 )
0,92 • 2 = 1,84 ( целая часть 1 )
1,84 • 2 = 1,68 ( целая часть 1 ) и т.д.
Ответ: 0.7310 = 0,10112

Конечная десятичная дробь
стала бесконечной (периодической) двоичной

счисления –
метод вычитания степеней.
Число 11410

114 – 26 = 114 – 64 = 50
50 – 25 = 50 – 32 = 18
18 – 24 = 2
2 – 21 = 0
26 25 24 23 22 21 20
1 1 1 0 0 1 0

Ответ: 11410 = 11100102

счисления, часто с целью уменьшения количества записываемых на бумаге

или вводимых с клавиатуры ПК знаков бывает удобнее пользоваться восьмеричными или шестнадцатеричными числами.

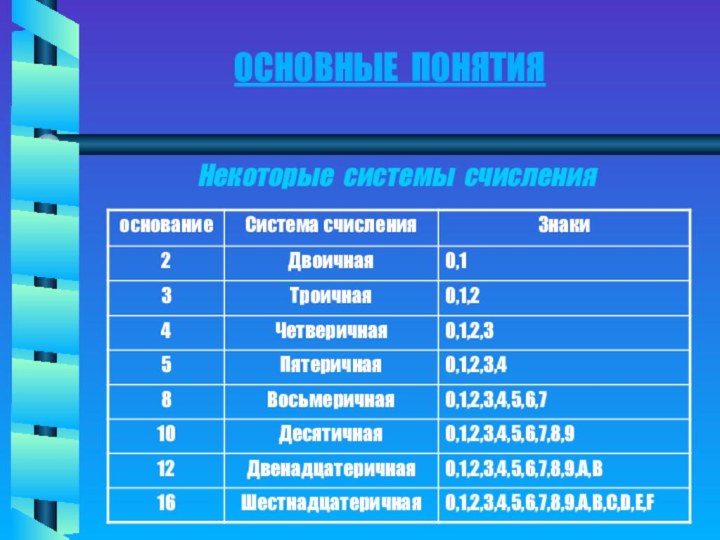
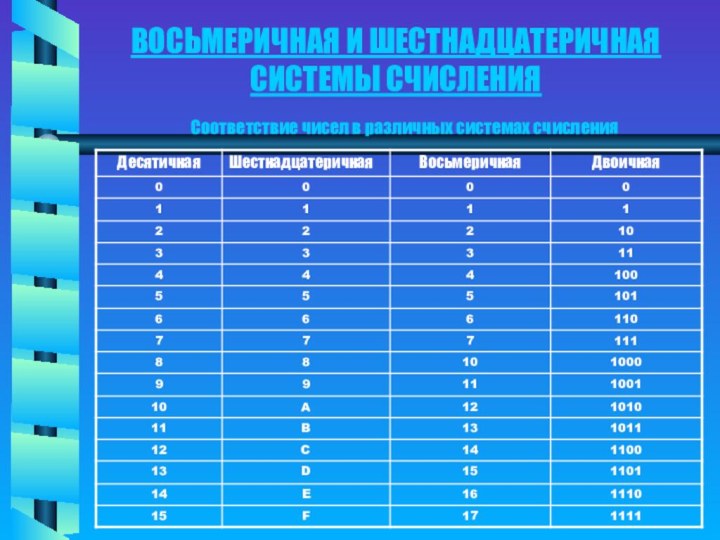
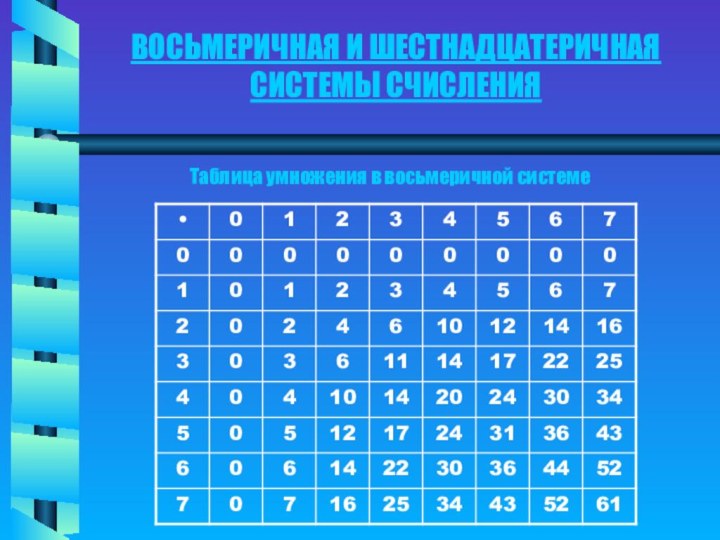
2. Восьмеричная и шестнадцатеричная системы
счисления

системы счисления в восьмеричную ( по аналогии с

двоичной системой счисления ) с помощью деления и умножения на 8 (в остатке только 0, 1, 2, 3, 4, 5, 6, 7 ).
Число 58,32 10
58/2=7 ( 2 в остатке)
7/8=0 ( 7 в остатке)
0,32•8=2,56
2,56•8=4,48
0,48•8=3,84 ...
Ответ: 58,3210 = 72,243...
Из конечной дроби в одной системе счисления получиться бесконечная дробь в другой.

системы счисления в шестнадцатеричную производиться аналогично ( в остатке

только 0,1,2,3,4,5,6.7,8,9,A,B,C,D,E,F ).
Число 58,410
58/16 = 3 ( 10 в остатке )
3/16 = 0 ( 3 в остатке )
0,4 • 16 = 6,4
0,4 • 16 = 6,4...
Ответ: 58,410 = 8 А, 66...16

Из конечной дроби в десятичной системе счисления получиться бесконечная дробь в шестнадцатеричной системе счисления.

системах счисления

в 8-е необходимо разбить его справа налево на группы

по 3 цифры, а затем каждой группе поставить в соответствие её 8-й эквивалент.

Пример: 110110012 = 11 011 001 ,
3 3 1
т.е. 110110012 = 3318
Ответ: 110110012 = 3318

Группу из трёх двоичных цифр называют «двоичной триадой».

в 16-е производиться путём разбиения данного числа на
группы

по 4 цифры – «двоичные тетрады».

Пример: 11000110110012 = 1 1000 1101 1001 ,
8 D 9
т.е. 11000110110012 = 18D916

Ответ: 11000110110012 = 18D916

чисел в 2-е производится обратным путём – сопоставлением каждому

знаку числа в соответствующей тройки (четвёрки) двоичных цифр.
Число 3318 и 18D916
Пример: 3318 38 - 112
38 - 0112
18 - 0012
Пример: 18D98 18 - 12
88 - 10002
D8 - 11012
98 - 10012

системе счисления. Алгоритм Горнера
Таблица сложения в восьмеричной системе

системе

а в строке ниже будем получать число в нужной

нам системе счисления.
Для этого первую цифру перепишем без изменения, а под каждой следующей цифрой будем писать число полученное сложением этой цифры с произведением слева стоящего числа на основание системы счисления.

100111011
0 0 1

1 1 0 1 1
1 2 4 9 19 39 78 157 315
1•2+0=2
2•2+0=4
4•2+1=9
9•2+1=19
19•2+1=39
39•2+0=78
78•2+1=157
157•2+1=315

системе счисления мы легко получим с помощью алгоритма Горнера

двоичные числа десятичных.