Презентация на тему Векторное программирование в планировании сельскохозяйственного производства

программирования
Пример задачи:
Товарищество, образованное тремя учредителями, имеет целью максимизацию дохода

каждого из учредителей.
Первый учредитель за свой счёт арендует для товарищества землю (b1), а присваивает только выручку от реализации зерна.
Второй приобретает за свой счёт удобрения (b2), а присваивает только выручку от реализации картофеля.
Третий получает и оплачивает кредит (b3), присваивает выручку от реализации капусты.
Известны потребности культур в удобрениях и в оборотном капитале (A), цены культур (c) и ресурсов (d).
Площади под названными культурами – x1, x2 и x3 соответственно.
Найти план, при котором каждый из участников товарищества получает максимальный доход.

программирования
x1+x2+x3 ≤ b1 – баланс земельных угодий, га
a21x1+a22x2+a22x3 ≤

b2 – баланс удобрений, т
a31x1+a32x2+a33x3 ≤ b3 – баланс оборотного капитала, тыс.руб.
max c1x1 – d1b1 – доход первого учредителя, тыс.руб.
max c2x2 – d2b2 – доход второго учредителя, тыс.руб.
max c3x3 – d3b3 – доход третьего учредителя, тыс.руб.
При таких обстоятельствах почти всегда существует множество решений, при которых каждая целевая функция оказывается в оптимуме.
Но эти решения не равноценны с позиций каждого из участников товарищества. Один из них предпочтёт одно решение, другой – другое. Не существует формального правила разрешения этого конфликта, если только участники сами не договорятся о каком-нибудь правиле.

программирования
Задача векторного программирования – это задача о нахождении оптимума

двух или более функций, удовлетворяющего условиям, заданным в форме уравнений и неравенств.
Решением задачи векторного программирования считается вектор таких значений её переменных, при которых нельзя улучшить значение ни одной целевой функции иначе, чем за счёт ухудшения другой целевой функции.

программирования
Решение задачи векторного программирования часто (особенно в экономических приложениях)

называют оптимумом по Парето
(в честь выдающегося итальянского экономиста XIX века, впервые сформулировавшего такую задачу и предложившего принцип неухудшения целевых функций).
Всю совокупность разных оптимумов по Парето одной и той же задачи векторного программирования часто называют множеством Парето или поверхностью Парето.

программирования в общем виде
Задача математического программирования:
max z(x)
f(x) ≤ b
x

≥ 0

Задача векторного программирования:
max z(x)
f(x) ≤ b
x ≥ 0

Скаляр

Вектор

программирования в общем виде
Задача линейного программирования:

max cx
Ax ≤ b
x

≥ 0

Линейная задача векторного программирования:
max Cx
Ax ≤ b
x ≥ 0

по Парето путём ранжирования целей
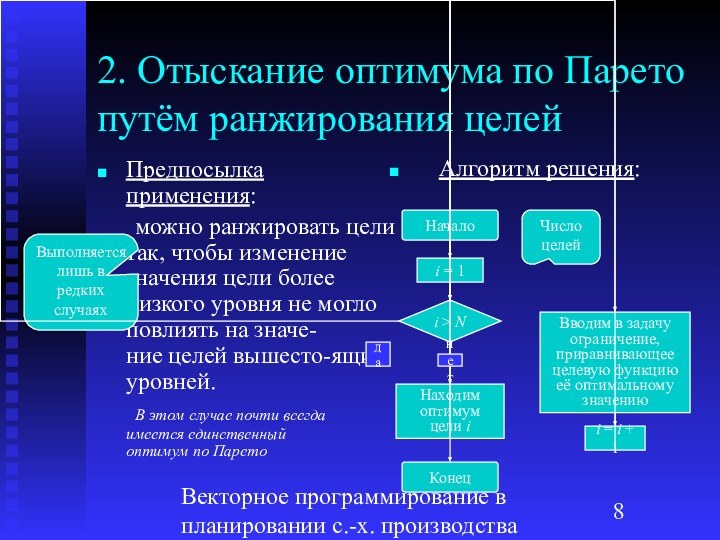
Предпосылка применения:
можно ранжировать цели так,

чтобы изменение значения цели более низкого уровня не могло повлиять на значе- ние целей вышесто-ящих уровней.
В этом случае почти всегда имеется единственный оптимум по Парето

Выполняется лишь в редких случаях

Алгоритм решения:

Число целей

по Парето путём ранжирования целей
Пример. Руководитель предприятия, выходящего из

кризиса, имеет следующие приоритеты:
Возвратить максимально возможную часть долгосрочного кредита.
Минимизировать сокращение поголовья коров основного стада.
Достичь максимально возможного уровня заработной платы одного работника.

по Парето путём ранжирования целей
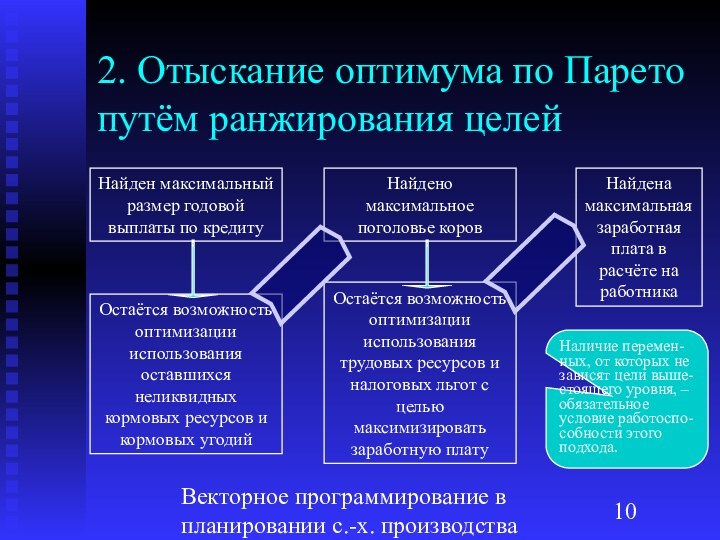
Найден максимальный размер годовой выплаты

по кредиту

Наличие перемен-ных, от которых не зависят цели выше-стоящего уровня, – обязательное условие работоспо-собности этого подхода.

по Парето путём ранжирования целей
Анализ двойственных оценок
Экономический смысл имеют

двойственные оценки, полученные после решения последней из N задач оптимизации.
Двойственные оценки дополнительных ограничений, отражающих цели более высоких уровней:
означают величину прироста цели уровня N при единичном сокращении значения данной цели;
не означают величину сокращения цели уровня N при единичном росте значения данной цели.
Двойственные оценки обычных ограничений отражают их влияние на целевую функцию самого низкого уровня.
Влияние ограничений на остальные целевые функции можно определить, поделив оценки ограничений на оценки дополнительных ограничений, заменивших целевые функции.

по Парето весовым методом
Предпосылка применения: тем или иным способом

могут быть обоснованы «цены», за которые одна цель может уступить место другой.
В этом случае векторное программирование сводится к обычному математическому программированию.

Алгоритм решения:
заменить вектор критериев Cx одним скалярным критерием (wC)x, где w — вектор весов.
решить получившуюся задачу математического программирования обычным способом.
Решение является одним из оптимумов по Парето исходной задачи.
Выбрав другой w, можно получить другой оптимум по Парето.

по Парето весовым методом
Пример: предположим, что в предыдущем примере

руководитель выходящего из кризиса предприятия определился с тем, что:
ради выплаты 10000 руб. долга он готов пожертвовать одной коровой;
ради одной коровы – 50 рублями заработной платы каждго своего работника в месяц.

по Парето весовым методом
Анализ двойственных оценок
Двойственные оценки отражают влияние

ограничений на функцию (wC)x в данном оптимуме по Парето.
Чтобы определить влияние ограничения на отдельно взятую цель в данном оптимуме по Парето, нужно разделить оценку ограничения на вес данной цели.

при неизменных пропорциях между целями
Предпосылка применения: цели являются абсолютно взаимо-дополняющими.
Алгоритм

решения:
в задачу вводится дополнительная переменная xZ;
вектор целевых функций заменяется вектором ограниче-ний Cx=xzw;
вводится новая целевая функция max xz.

w – вектор заданных пропорций между целями

при неизменных пропорциях между целями
Пример: найти наилучший план для

следующих условий:
Сельскохозяйственная организация стремится максимизировать запас каждого вида активов.
Активы для их производительного использования должны быть в наличии в определённых пропорциях.
Эти пропорции известны из практики.
Известна зависимость прироста активов каждого вида от имеющихся способов их производственного использования.

при неизменных пропорциях между целями
Анализ
Если двойственные оценки всех ограничений,

представляющих цели, оказались ненулевыми, то решение представляет собой оптимум по Парето.
Результат решения не обязательно является оптимумом по Парето.
Чтобы определить влияние ограничения на какую-либо цель, необходимо разделить оценку данного ограничения на оценку ограничения, представляющего данную цель.

по Парето при заданных уровнях насыщения (Target oriented programming)

Предпосылка применения: известны уровни насыщения некоторых или всех целей.
Недостаток: остаётся нерешённым вопрос, какая из целей должна приближаться к насыщению в первую очередь.
Достоинство: уровни насыщения отсекают часть множества Парето, так что исследовать оставшуюся часть оказывается проще.

Алгоритм решения
Для каждой цели с известным уровнем насыщения вводятся:
дополнительная переменная по отклонению значения цели от уровня насыщения;
уравнение по её расчёту;
целевая функция по минимизации дополнительной переменной.
Полученная задача решается одним из предыдущих способов.

Как преодолеть недостаток?

по Парето при заданных уровнях насыщения
Пример 1
В примере о

предприятии, преодолевающем кризис, имеются естественные пределы насыщения первых двух целей:
размер непогашенного кредита – 0,
поголовье коров, равное числу имеющихся скотомест.
Пример 2
Предприятие, действующее в условиях олигополии, максимизирует:
объём продаж – безусловно;
прибыль – но только до уровня, достаточного для обеспечения воспроизводственного процесса.
Метод анализа двойственных оценок зависит от используемого способа скаляризации вектора целевых функций (см. вопросы 2-4).

систем
В конкурентной системе каждому хозяйствующему субъекту соответствуют:
набор подконтрольных ему

переменных;
собственная целевая функция
при наличии балансов общих для всех ресурсов.
Каждый хозяйствующий субъект характеризуется уже достигнутым им значением целевой функции.
Хозяйствующий субъект не будет влиять на подконтрольные ему переменные таким образом, чтобы его целевая функция снижалась.
В результате действий хозяйствующих субъектов, соответствующих предыдущему правилу, рано или поздно достигается некоторый оптимум по Парето.

систем
Цель планирования в этих условиях – обеспечить переход конкурентной

системы в оптимум по Парето, желательный для органа управления. Например:
оптимум, в котором все целевые функции хозяйствующих субъектов возрастут в одной и той же степени – максимально достижимой
(метод – векторная оптимизация при неизменных пропорциях между целями);
оптимум, в котором в первую очередь максимизируются целевые функции, имеющие наименьшие значения
(метод – оптимизация при заданных уровнях насыщения);
оптимум, в котором достигает максимума собственная целевая функция управляющего органа при условии, что целевые функции хозяйствующих субъектов будут не ниже фактических уровней (быть может, увеличенных на некоторый коэффициент)
(метод – максимизация целевой функции органа управления при ограничениях по минимально допустимым значениям остальных целевых функций).
Цель достигается за счёт воздействия на переменные, подконтрольные органу управления.