- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку информатики Рекурсивные алгоритмы
Содержание
- 2. ТеорияРекурсия вокруг насРекурсия в математикеПрограммированиеЗадачи на закреплениеСписок использованной литературыСодержание
- 3. Реку́рсия (RECURCIО - возвращение) — определение, описание,
- 4. Что нужно знать:Рекурсия может быть прямой и
- 5. Рекурсия может быть прямой и косвенной.В
- 6. Косвенная рекурсия создаётся за счёт вызоваданной функции
- 7. Уроборос – змей, кусающий свой собственный хвост.
- 8. Рассказ из С.Лева «Кибериады» о разумной машине,
- 9. Первым романом, удивившим читателей приемом рекурсии, был
- 10. Рекурсия вокруг нас… У попа была собака,
- 11. Рекурсия вокруг нас… А. Блока
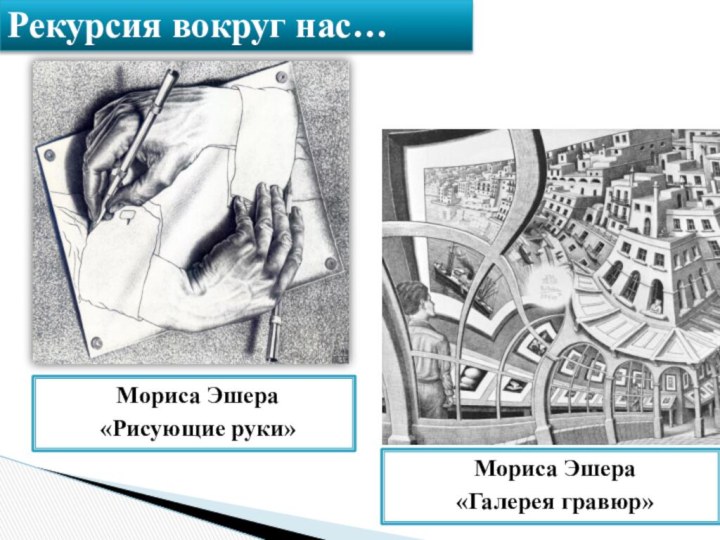
- 12. Мориса Эшера «Рисующие руки»Мориса Эшера «Галерея гравюр»Рекурсия вокруг нас…
- 13. Рекурсия вокруг нас… Фрактал "Треугольник Серпинского" Эйфелева Башня в ПарижеИсторический музей в Москве
- 14. Рекурсия вокруг нас… Дерево состоит из веток.
- 15. Эффект Дросте - термин для изображения специфического
- 16. Рекурсия вокруг нас… Герб Российской Федерацииявляется рекурсивно-определённым
- 17. Рекурсия в математике1) Арифметическая прогрессия: а)а1=а0; б) аn=аn-1+d.2) Геометрическая прогрессия: а) а1=а0; б) аn=а n-1*q.
- 18. Рекурсия в математике3) Факториал an=n!
- 20. ПрограммированиеРекурсия — это такой способ организации вспомогательного
- 21. В языке программирования Pascal рекурсивностью могут обладать
- 22. Пример рекурсивной процедуры: Program n1; uses crt;
- 23. Вызов Rec(5)Вызов Rec(4)Вызов Rec(3)Вызов Rec(2)Вызов Rec(1)Вывод (1)Вывод
- 24. ПрограммированиеЗадание1. Алгоритм вычисления значения функции F(n), где
- 25. Задание 2. Дан рекурсивный алгоритм:procedure F(n: integer);begin
- 26. Задание 3. Дан рекурсивный алгоритм:procedure F(n: integer);begin
- 27. Задание 4. Дан рекурсивный алгоритмprocedure F(n: integer);begin
- 28. Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n
- 29. Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n
- 30. Задание 6. Дан рекурсивный алгоритмprocedure F(n: integer);begin if n
- 31. Задание 7. Дан рекурсивный алгоритмprocedure F(n: integer);begin if n
- 32. Задание 8. Дан рекурсивный алгоритмprocedure F(n: integer);begin
- 33. Задание 9. Дан рекурсивный алгоритмprocedure F(n: integer);Begin
- 34. Задание 10. Даны два рекурсивных алгоритмаprocedure F(n:
- 35. Задача 1. Дан рекурсивный алгоритмprocedure F(n: integer);Begin writeln(n); if n
- 36. Задача 2. Дан рекурсивный алгоритмprocedure F(n: integer);Begin
- 37. ПрограммированиеЗадачи на закреплениеЗадача 3. Даны два рекурсивных
- 38. ПрограммированиеЗадачи на закреплениеЗадача 4. Даны два рекурсивных
- 39. ПрограммированиеЗадачи на закреплениеЗадача 5. Даны два рекурсивных
- 40. ПрограммированиеЗадачи на закреплениеЗадача 6. Даны два рекурсивных
- 41. ПрограммированиеЗадачи на закреплениеЗадача 7. Даны два рекурсивных
- 42. ПрограммированиеЗадачи на закреплениеЗадача 8. Даны два рекурсивных
- 44. Список использованной литературыКрылов С.С ЕГЭ 2017. Информатика
- 45. Слайд 1, 2 http://arxweb.net/pictures/raznoe/recursia.jpegСлайд 3-7,17,18,20-36, 44 https://upload.wikimedia.org/wikipedia/commons/b/b3/Screenshot_Recursion_via_vlc.pngСлайд
- 46. Скачать презентацию
- 47. Похожие презентации








































Слайд 2
Теория
Рекурсия вокруг нас
Рекурсия в математике
Программирование
Задачи на закрепление
Список использованной
литературы
Слайд 3 Реку́рсия (RECURCIО - возвращение) — определение, описание, изображение
какого-либо объекта или процесса внутри самого этого объекта или
процесса, то есть ситуация, когда объект является частью самого себя.Теория
Рекурсивным называется любой объект, который частично определяется через себя.
Слайд 4
Что нужно знать:
Рекурсия может быть прямой и косвенной.
Рекурсия
– это приём, позволяющий свести исходную задачу к одной
или нескольким более простым задачам того же типа.Чтобы определить рекурсию, нужно задать:
-условие остановки рекурсии
-рекуррентную формулу
Любую рекурсивную процедуру можно запрограммировать с помощью цикла
Рекурсия позволяет заменить цикл и в некоторых сложных задачах делает решение более понятным, хотя часто менее эффективным.
Теория
Слайд 5
Рекурсия может быть прямой и косвенной.
В случае
прямой рекурсии вызов функцией самой себя делается непосредственно в
этой же функцииprocedure F(n: integer);
begin
writeln(n);
if n > 1 then begin
F(n-1);
F(n-3)
end
end;
end;
Теория
Слайд 6
Косвенная рекурсия создаётся за счёт вызова
данной функции из
какой-либо другой функции,
которая сама вызывалась из данной функции.
function
F(n: integer): integer;begin
if n > 2 then F := F(n - 1) + G(n - 2)
else F := 1;
end;
function G(n: integer): integer;
begin
if n > 2 then G := G(n - 1) + F(n - 2)
else G := 1;
end;
Теория
Слайд 7 Уроборос – змей, кусающий свой собственный хвост. Это
древний символ бесконечности Вселенной и времени, круговорота жизни, отождествляемых
с рекурсией.Рекурсия вокруг нас…
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Классическим примером конечной рекурсии является русская матрешка.
Слайд 8 Рассказ из С.Лева «Кибериады» о разумной машине, которая
обладала достаточным умом и ленью, чтобы для решения поставленной
задачи построить себе подобную, и поручить решение ей. (бесконечная рекурсия - каждая новая машина строила себе подобную).Рекурсия вокруг нас…
Н.В. Гоголь в повести «Портрет» описывает сон художника Черткова (сон третьего уровня рекурсии). Проснувшись от этого сна Чертков попадает на второй уровень рекурсии – во второй сон. Проснувшись от второго сна, он попадает в первый сон, от которого тоже придется проснуться.
"Мастер и Маргарита" - один из наиболее ярких рекурсивных романов.
Тема Иешуа и Пилата рекурсивно вызывается из темы Мастера и Маргариты. Кроме того, здесь так же используется прием "книга в книге". Мастер пишет роман об Иешуа и Пилате, текст которого сливается с текстом книги "Мастер и Маргарита".
Слайд 9 Первым романом, удивившим читателей приемом рекурсии, был "Дон
Кихот". Сервантес все время пытался смешивать два мира: мир
читателя и мир книги. У Сервантеса главный процесс не просто книга, но книга плюс читатель. В шестой главе цирюльник, осматривая библиотеку Дон Кихота, находит книгу Сервантеса и высказывает суждения о писателе. Вымысел Сервантеса рассуждает о нем. В начале девятой главы сообщается, что роман переведен с арабского и что Сервантес купил его на рынке. Наконец, во второй части романа персонажи уже прочли первую часть.Рекурсия вокруг нас…
Элементы использования рекурсии находим еще раньше у Шекспира. Гамлет ставит спектакль, где в упрощенном варианте описываются события трагедии.
В романее Л. Толстого «Война и мир» рекурсия отражает прошлое в настоящем и будущем.
Слайд 10
Рекурсия вокруг нас…
У попа была собака, он
её любил Она съела кусок мяса, он её убил В землю
закопал, Надпись написал: «У попа была собака, он её любил Она съела кусок мяса, он её убил В землю закопал, Надпись написал:Р. Бернс «Дом, который построил Джек» в переводе
С. Маршака
Вот дом,
Который построил Джек.
А это пшеница,
Которая в темном чулане хранится
В доме,
Который построил Джек
А это веселая птица-синица,
Которая часто ворует пшеницу,
Которая в темном чулане хранится.
Слайд 11
Рекурсия вокруг нас…
А. Блока
Ночь, улица, фонарь,
аптека. Бессмысленный и тусклый свет. Живи еще хоть четверть века – Все
будет так. Исхода нет. Умрешь – начнешь опять сначала, И повторится все, как встарь: Ночь, ледяная рябь канала, Аптека, улица, фонарь.
Слайд 13
Рекурсия вокруг нас…
Фрактал
"Треугольник Серпинского"
Эйфелева Башня
в Париже
Исторический музей в Москве
Слайд 14
Рекурсия вокруг нас…
Дерево состоит из веток. Ветка
в свою очередь состоит из более маленьких веточек. Каждая
ветка повторяет дерево.Реки образуются из впадающих в них рек.
Чешуя шишек и семена некоторых цветов (например, подсолнечника) расположены пересекающимися
спиралевидными веерами, определяемыми соотношением чисел Фибоначчи.
Слайд 15 Эффект Дросте - термин для изображения специфического вида
рекурсивного изображения. Изображение включает уменьшенный собственный вариант самого себя.
Этот более малый вариант после этого показывает даже более малый вариант себя, и так далее. Практически это продолжается пока разрешение изображения позволяет уменьшает размер. Термин был введен в честь Дросте, голландского какао.Рекурсия вокруг нас…
Слайд 16
Рекурсия вокруг нас…
Герб Российской Федерации
является рекурсивно-определённым графическим
объектом: в правой лапе изображённого на нём двуглавого орла
зажат скипетр, который венчается уменьшенной копией герба. Так как на этом гербе в правой лапе орла также находится скипетр, получается бесконечная рекурсия.
Слайд 17
Рекурсия в математике
1) Арифметическая прогрессия:
а)а1=а0;
б) аn=аn-1+d.
2)
Геометрическая прогрессия:
а) а1=а0;
б) аn=а n-1*q.
Слайд 18
Рекурсия в математике
3) Факториал
an=n!
n!=1*2*3*4*5*б*...*n.
а)а1=1;
б) аn=n*аn-1.
4) Числа Фибоначчи.
x1=x2=1
xn=xn-1+xn-2
при n > 2 Каждый элемент ряда Фибоначчи является суммой двух предшествующих элементов, т.е. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…
Слайд 20
Программирование
Рекурсия — это такой способ организации вспомогательного алгоритма
(подпрограммы), при котором эта подпрограмма (процедура или функция) в
ходе выполнения ее операторов обращается сама к себе.В программировании рекурсия — вызов функции из неё же самой, непосредственно или через другие функции, например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Слайд 21
В языке программирования Pascal
рекурсивностью могут обладать как
функции, так и процедуры.
Примеры рекурсивной процедуры.
Общая форма записи:
Procedure Rec (a:integer);
Begin
If a>0 Then Rec(a-1);
Writeln(a);
End;
Программирование
Важно!
Выполнение рекурсивного алгоритма можно представить следующим образом:
каждый рекурсивный вызов процедуры F порождает в памяти компьютера новую копию этой процедуры и запускает ее на выполнение со своими значениями входных параметров.
После того как процедура F завершила работу, выполнение программы продолжается со следующего оператора после вызова F.
Слайд 22
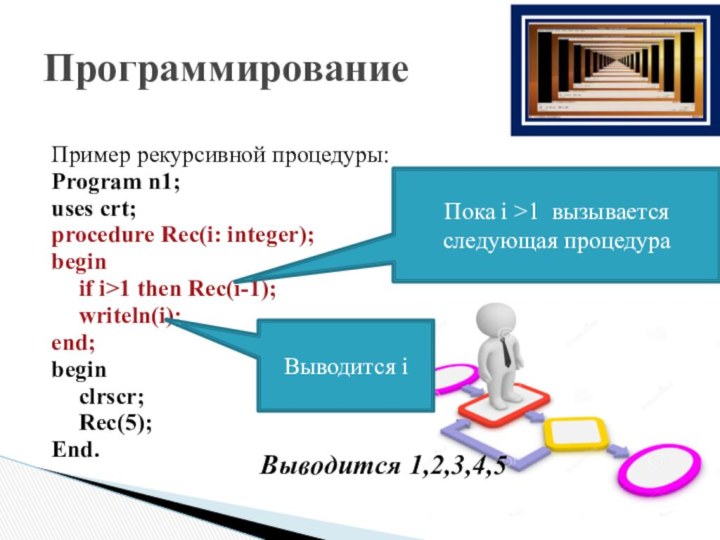
Пример рекурсивной процедуры:
Program n1;
uses crt;
procedure
Rec(i: integer);
begin
if i>1 then Rec(i-1);
writeln(i);
end;
begin
clrscr;
Rec(5);
End.
Программирование
Выводится 1,2,3,4,5
Пока i >1 вызывается следующая процедура
Выводится i
Слайд 23
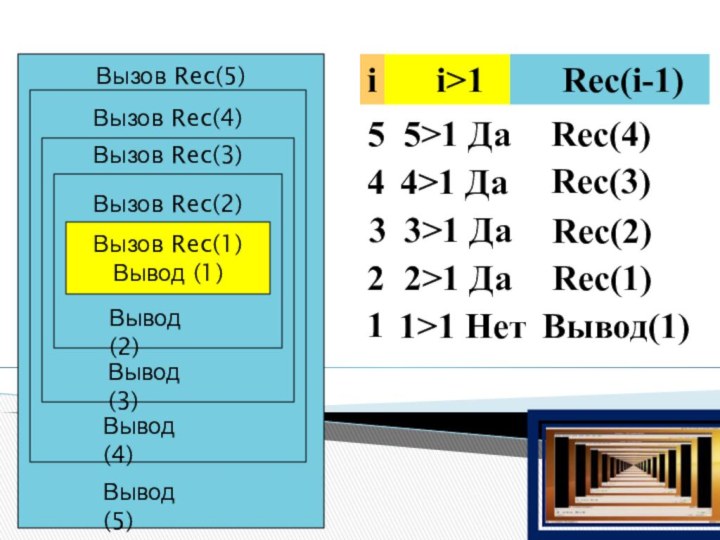
Вызов Rec(5)
Вызов Rec(4)
Вызов Rec(3)
Вызов Rec(2)
Вызов Rec(1)
Вывод (1)
Вывод (2)
Вывод
(3)
Вывод (4)
Вывод (5)
i>1
i
Rec(i-1)
5
4
3
2
1
5>1 Да
4>1 Да
3>1 Да
2>1 Да
1>1 Нет
Rec(4)
Rec(3)
Rec(2)
Rec(1)
Вывод(1)
Слайд 24
Программирование
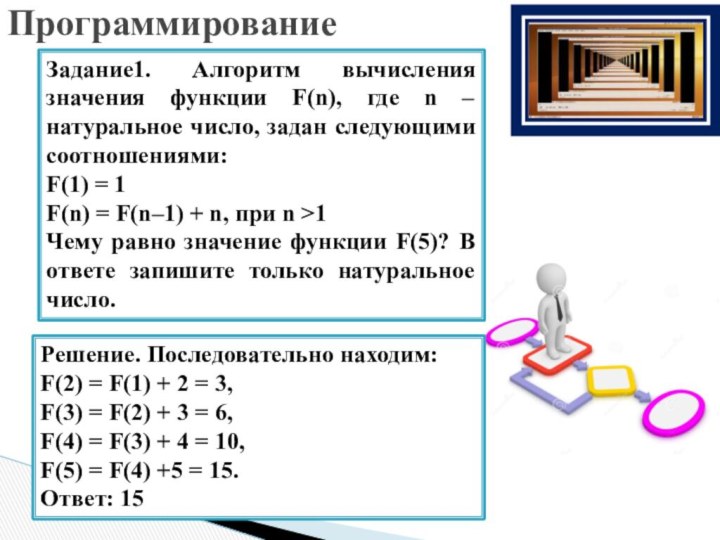
Задание1. Алгоритм вычисления значения функции F(n), где n
– натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) + n, при n >1
Чему равно значение функции F(5)? В ответе запишите только натуральное число.
Решение. Последовательно находим:
F(2) = F(1) + 2 = 3,
F(3) = F(2) + 3 = 6,
F(4) = F(3) + 4 = 10,
F(5) = F(4) +5 = 15.
Ответ: 15
Слайд 25
Задание 2. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 5 then begin
F(n +
1);F(n + 3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
Программирование
Складывая все эти числа, получаем 49
Слайд 26
Задание 3. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 6 then begin
F(n+2);
F(n*3)end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
Программирование
Складывая все эти числа, получаем 79
Слайд 27
Задание 4. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if
n < 3 then
write('*')
else begin
F(n-1);F(n-2);
F(n-2)
end;
end;
Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.
Программирование
Решение:
Найдем значение процедуры:
F(6)=F(5)+2*F(4)
F(5)=F(4)+2*F(3)
F(4)=F(3)+2*F(2)
F(3)=F(2)+2*F(0)=F(2)+2*1=F(2)+2
F(2)=1
Следовательно:
F(3)=1+2=3
F(4)=3+2*1=5
F(5)=5+2*3=11
F(6)=11+2*5=21
Слайд 28 Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n);
if n
+1); end end; Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(2)?Программирование
F(2)
F(4)
F(3)
F(8)
F(5)
F(4)
F(6)
F(8)
F(5)
8+4+5+2+3+4+6+8+5=45
!
Построенное дерево позволяет ответить на более сложный вопрос: «Что напечатает программа?»
Выписав значения узлов в порядке построения, получим:
2 4 8 5 3 6 4 8 5
Результат работы программы при ином расположении оператора печати n, в общем случае, отличается от данного.
Слайд 29 Задание 5. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n);
if n
+1); end end; Чему равна сумма всех чисел, напечатанных на экране при выgолнении вызова F(2)?Программирование
Решение (II способ):
При n<=4
F(n)=n+F(2n)+F(n+1)
При n>4
F(8)=8; F(7)=7; F(6)=6; F(5)=5
Найдем значение процедуры:
F(4)=4 +F(2*4)+F(4+1)=4+F(8)+F(5)=
=4+8+5=17
F(3)=3 +F(2*3)+F(3+1)=3+F(6)+F(4)=
=3+6+17=26
F(2)=2 +F(2*2)+F(2+1)=2+F(4)+F(3)=
=2+17+26=45
Слайд 30
Задание 6. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n
F(n*2);F(n+1);
end;
write(n);
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(2).
Программирование
Решение:
при n<=4 F(n)=F(2n)+F(n+1)+n
при n>4 F(n)=n
Найдем значение процедуры:
F(2)=F(2*2)+F(2+1)+2=F(4)+F(3)+2
F(3)=F(2*3)+F(3+1)+3=F(6)+F(4)+3
F(4)=F(2*4)+F(4+1)+4=F(8)+F(5)+4
F(2)=F(8)+F(5)+4+F(6)+F(8)+F(5)+4+3+2
Ответ:
8,5,4,6,8,5,4,3,2
Слайд 31
Задание 7. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n
F(n*2);write(n);
F(n+1);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(2).
Программирование
Решение:
при n<=4 F(n)=F(2n)+n +F(n+1)
при n>4 F(n)= «не печатает!»
Найдем значение процедуры:
F(2)=F(2*2)+2+F(2+1)=F(4)+2+F(3)
F(3)=F(2*3)+3+F(3+1)=F(6)+3+F(4)
F(4)=F(2*4)+4+F(4+1)=F(8)+4+F(5)
F(2)=4+2+F(3)=4+2+3+F(4)=4+2+3+4
Ответ:
4,2,3,4
Слайд 32
Задание 8. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n >1 then
begin
F(n-2);write(n);
F(n div 2);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(6).
Программирование
Решение:
при n>1 F(n)=F(n-2)+n +F(n div 2)
при n<=1 F(n)= «не печатает!»
Найдем значение процедуры:
F(6)=F(6-2)+6+F(6 div 2)=F(4)+6+F(3)
F(4)=F(4-2)+4+F(4 div 2)=F(2)+4+F(2)
F(3)=F(3-2)+3+ F(3 div 2)=F(1)+3+F(1)
F(2)=F(2-2)+2+ F(2 div 2)=F(0)+2+F(1)
F(6)=F(2)+4+F(2)+6+F(3)= =F(2)+4+F(2)+6+3=2+4+2+6+3
Ответ:
2,4,2,6,3
Слайд 33
Задание 9. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
write(n);
if n >1 then
begin
F(n-2);F(n div 2);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(5).
Программирование
Решение:
при n>1 F(n)=n+F(n-2) +F(n div 2)
при n<=1 F(n)=n
Найдем значение процедуры:
F(5)=5+F(5-2)+F(5 div 2)=5+F(3)+F(2)
F(3)=3+F(3-2)+F(3 div 2)=3+F(1)+F(1)
F(2)=2+F(2-2)+F(2 div 2)=2+F(0)+F(1)
Получим:
F(2)=2+0+1
F(3)=3+1+1
F(5)=5+3+1+1+2+0+1
Ответ: 5,3,1,1,2,0,1
Слайд 34
Задание 10. Даны два рекурсивных алгоритма
procedure F(n: integer);
forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);
if n >0 then F(n-2) else G(n);end;
procedure G(n: integer);
Begin
write(‘**’); if n >1 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(20)?
Программирование
Решение:
при n>10 F(n)=‘*’+F(n-2)
при n<=10 F(n)=‘**’ +F(n-3)
при n<=1 G(n)=‘**’
Найдем значение процедуры:
F(20)=* +F(18)
F(18)=* +F(16)
F(16)=* +F(14)
F(14)=* +F(12)
F(12)=* +F(10)
F(10)=* + ** +F(7)
F(7)=* + ** +F(4)
F(4)=* + ** +F(1)
F(1)=* + **
Ответ: 17
F(1)=3
F(4)=3+3=6
F(7)=3+6=9
F(10)=3+9=12
F(12)=1+12=13
F(14)=1+13=14
F(16)=1+14=15
F(18)=1+15=16
F(20)=1+16=17
Слайд 35
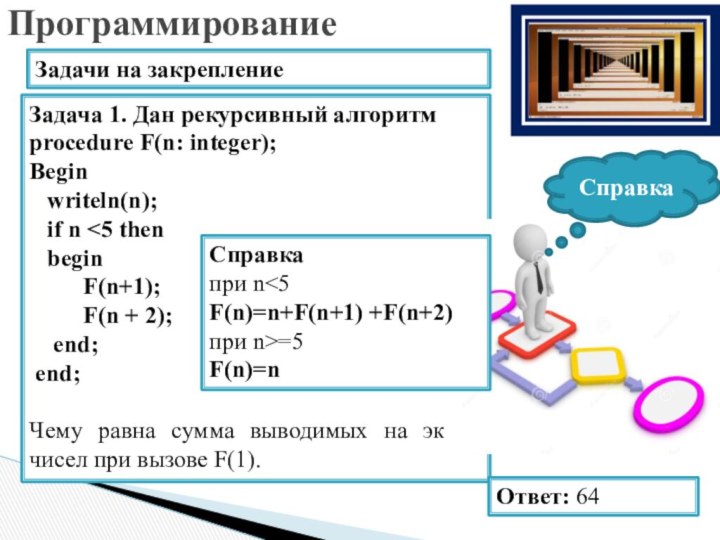
Задача 1. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
writeln(n);
if n
F(n+1);F(n + 2);
end;
end;
Чему равна сумма выводимых на экран чисел при вызове F(1).
Программирование
Ответ: 64
Задачи на закрепление
Справка
при n<5
F(n)=n+F(n+1) +F(n+2)
при n>=5
F(n)=n
Справка
Слайд 36
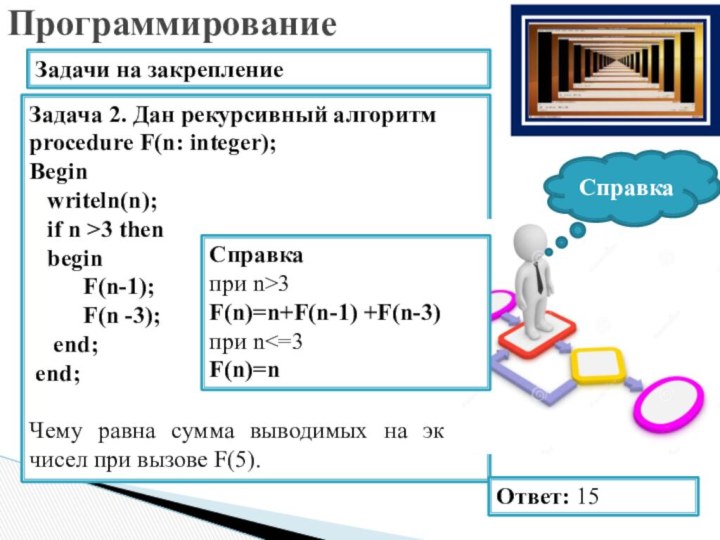
Задача 2. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
writeln(n);
if n >3 then
begin
F(n-1);F(n -3);
end;
end;
Чему равна сумма выводимых на экран чисел при вызове F(5).
Программирование
Ответ: 15
Задачи на закрепление
Справка
при n>3
F(n)=n+F(n-1) +F(n-3)
при n<=3
F(n)=n
Справка
Слайд 37
Программирование
Задачи на закрепление
Задача 3. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);if n >10 then F(n-2) else G(n);
end;
procedure G(n: integer);
Begin
write(‘**’); if n >0 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(18)?
Ответ: 19
Слайд 38
Программирование
Задачи на закрепление
Задача 4. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);if n >=2 then F(n-2) else G(n);
end;
procedure G(n: integer);
Begin
write(‘**’); if n >1 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(22)?
Ответ: 18
Слайд 39
Программирование
Задачи на закрепление
Задача 5. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n);if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n); if n >0 then F(n);
end;
Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?
Ответ: 40
Слайд 40
Программирование
Задачи на закрепление
Задача 6. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n mod 2);if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n); if n >0 then F(n);
end;
Какова сумма чисел, напечатанных на экране при выполнении вызова F(19)?
Ответ: 16
Слайд 41
Программирование
Задачи на закрепление
Задача 7. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n mod 2);if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n mod 2); if n >0 then F(n);
end;
Сколько нулей будет выведено на экране при выполнении вызова F(21)?
Ответ: 5
Слайд 42
Программирование
Задачи на закрепление
Задача 8. Даны два рекурсивных алгоритма
procedure
F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
if n mod 5 =0 then G(n -5)else F(n-3);
end;
procedure G(n: integer);
Begin
write(‘*’); if n >0 then F(n-1);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(51)?
Ответ: 4
Слайд 44
Список использованной литературы
Крылов С.С ЕГЭ 2017. Информатика Тематические
тестовые задания/С.С. Крылов, Д.М. Ушаков.-М.:Издательство «Экзамен», 2017
Крылов С.С, Чуркина
Т.Е. ЕГЭ. Информатика и ИКТ: типовые экзаменационные варианты: 20 вариантов. -М.:Издательство «Национальное образование», 2017Бражникова О.В. Рекурсия. Рекурсивные алгоритмы http://easyen.ru
Исламов Р.Г. «Рекурсивные алгоритмы». Разбор заданий №11 ЕГЭ по информатике и ИКТ
Коротун О.В. Рекурсивные алгоритмы. Задание 11 ЕГЭ. http://proteacher.ru/2015/01/10/Rekursivnye_algoritmy_1420913156_12749.pptx
Юдин А.Б. Рекрусия http://www.uchportal.ru/load/18-1-0-55354
Слайд 45
Слайд 1, 2 http://arxweb.net/pictures/raznoe/recursia.jpeg
Слайд 3-7,17,18,20-36, 44 https://upload.wikimedia.org/wikipedia/commons/b/b3/Screenshot_Recursion_via_vlc.png
Слайд 3
http://lols.ru/uploads/posts/2011-07/1309983680_1309964j.jpg
Слайд 7 Змей http://ezolan.ru/image/cache/data/Talisman/smola/kumirnica/95-500x500.jpg
Зеркала http://cdn01.ru/files/users/images/92/44/92443e52bffa0b4f29b8075eb6a50193.jpg
Матрешки https://image.jimcdn.com/app/cms/image/transf/none/path/seb6ba021dbaf218c/image/i0b5fd1e834074150/version/1418029668/image.jpg
Слайд 8 Лем http://tomuz.ru/uploads/images/l/e/m/lem_stanislav_kiberiada_01_skazki_robotov.jpg
Портрет
https://fs00.infourok.ru/images/doc/233/91173/2/img4.jpgМастер и Маргарита http://biblus.ru/pics/7/f/f/1005817671.jpg
Слайд 9
Гамлет http://botinok.co.il/sites/default/files/images/c44e9d5e0c2582fb3bfd9c60e1e36ea5_smoktunovskiy_gamlet.jpg
Дон Кихот https://upload.wikimedia.org/wikipedia/commons/thumb/a/ac/Honoré_Daumier_017_%28Don_Quixote%29.jpg/416px-Honoré_Daumier_017_%28Don_Quixote%29.jpg
Война и мир http://www.abbyreader.ru/pic/fa649070809c3dfb3fa768b4d8fd528a.jpg
Слайд 10
Поп http://cdn01.ru/files/users/images/e4/31/e4311658d876f53c249807107fc54648.jpg
Джек http://s-marshak.ru/books/d/d27/d27_02.jpg
Слайд 11 https://lh3.googleusercontent.com/-SqgOCQ0nNsk/TKnKgCfpcKI/AAAAAAAAHe4/1E4isRsTzeEJBdFNBeDLDEp_RRH-VHnEgCHM/s800/0_2910a_67b4058a_XL.jpg
Интернет-ресурсы




























