Презентация на тему по информатике на тему Основы логики(практика)

делителем числа 198,
б) x=Иркутск – столица

Франции.
в) сформулировать на обычном языке высказывания:
A = ¬S; B = x & s; C=sx; D = s  ¬ x; M = x s. Определить
их истинность. (Решение)
2. Пусть n=1, m=0. Определить истинность высказывания
(Решение)
3. Построить таблицу истинности выражений:

(Решение)

= (A  B) & (¬ A  ¬

B).
5. Построить таблицу истинности следующих выражений:

6. ЗАДАЧИ ЕГЭ ПО ИНФОРМАТИКЕ

А3

А10

В15

Решение

– столица Франции, а число 3 является делителем числа

198. (ложь).
Число 3 является делителем числа 198, или Иркутск – столица Франции. (истина).
Если число 3 является делителем числа 198, то Иркутск – не столица Франции. (истина).
Иркутск – столица Франции тогда и только тогда, когда число 3 является делителем числа 198. (ложь)

F:
Какое выражение соответствует F?
1) x1 ∨ x2 ∨ x3

∨ ¬x4 ∨ ¬x5 2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 4) ¬x1 ∧ x2 ∧ x3 ∧ x4 ∧ ¬x5

Пример решения

Посмотрим внимательно на ответы. Они представляют собой либо конъюнкцию, либо дизъюнкцию данных пяти переменных или отрицательных к ним.
Сначала выясним, конъюнкция это или дизъюнкция.
 Дизъюнкция не может принимать значение ноля дважды из трех разных комбинаций, следовательно, в ответе должна быть конъюнкция. Вычеркиваем 1 и 2 варианты ответа.
Из 3 и 4 вариантов подходит 4. Правильный ответ 4.

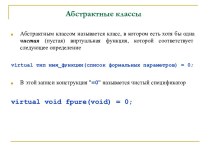
переменных x1, x2, x3, x4, x5, y1, y2, y3,

y4, y5, которые удовлетворяют всем перечисленным ниже условиям? 
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1
x1 ∨ y1 = 1
 В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Пример решения.

1) Из последнего уравнения следует, что глобально мы имеем три варианта x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.
2) Логическое И истинно, только тогда, когда истины все утверждения, а импликация ложна только в случае, если из истинного следует ложное.
3) Уравнение (1) описывает ряд переменных {x1, x2, x3, x4, x5}. Так как из переменной с более низким номером всегда следует переменная с более высоким, если любую переменную из этого ряда приравнять 1, то все следующие должны также быть равны 1. Для уравнения (2) существует то же самое правило. Иначе говоря, если записать переменные x (или y) в порядке возрастания их номеров, слева будут нули, а справа единицы.
4) Рассмотрим вариант x1=1, y1=1. Так как первые числа каждого ряда равны 1, то все следующие тоже равны 1. Существует только одна комбинация для этого варианта.
5) Рассмотрим вариант x1=0, y1=1. Для ряда все переменные равны 1, для x же существует 5 комбинаций, так как в ряде x может быть от 1 до 5 нолей включительно.
6) Последний вариант рассмотрим аналогично предыдущему. Там существует всего 5 комбинаций.
 
Правильный ответ: 5+5+1=11 комбинаций.