Презентация на тему Что такое системы счисления?

чисел с помощью символов. Такие символы в любой системе

счисления называются цифрами.
Алфавит системы счисления – это совокупность символов, используемых в данной системе счисления.

зависит от ее позиции в записи числа.
Н-р: римская

система счисления, алфавитная система счисления.

Римская система счисления
I V X L C D M
1 5 10 50 100 500 1000

Система счисления, в которой значение цифры зависит от ее позиции в записи числа.
К позиционным системам счисления относятся десятичная, двоичная, восьмеричная, двенадцатеричная, шестнадцатеричная и др. Основание позиционной системы счисления (q) – количество символов, используемых для записи числа.

системы счисления в десятичную – LXXXVI. XLIX. CMXCIX.
2. Запишите

десятичные числа в римской системе счисления – 464, 390, 2648.
3. Где в настоящее время используется римская система счисления.

3005,234; 185,7948; 11022; 1345,526; 112,0113; 16,5455.

q, представляются с помощью одной цифры данной системы. Если

число больше или равно q, то требуется две и более цифр.

Представление первых чисел
в некоторых системах счисления

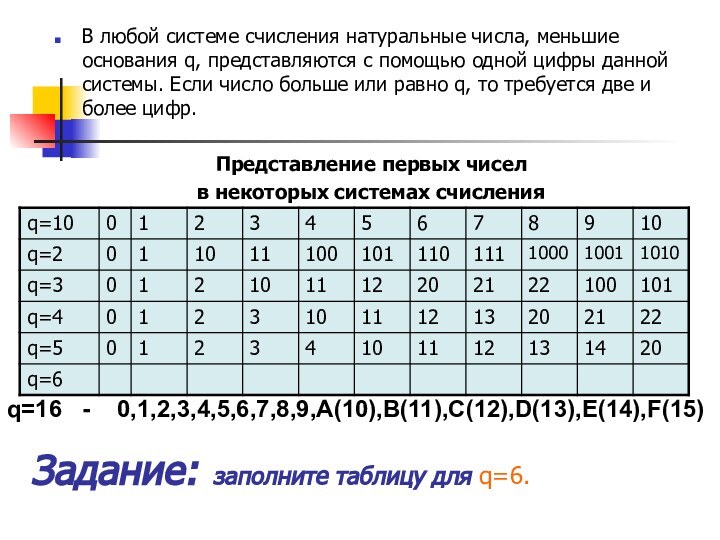
Задание: заполните таблицу для q=6.

q=16 - 0,1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14),F(15)

2 1 0 -1

-2
N10 = 3 4 8, 1 2 = 3*102 + 4*101 + 8*100 + 1*10-1 + 2*10-2

Свернутая форма записи числа развернутая форма записи числа

Любое действительное число можно записывать в любой позиционной системе счисления в виде суммы положительных и отрицательных степеней числа q (основания системы).

Задание5: Запишите в развернутой форме числа: N8=7764,1= N5=2430,43=

Задание6: Запишите число в десятичной системе счисления: 110112=……, 423,15=……, 5А,12116=…….

Пример:
1011,012=1*23+0*22+1*21+1*20+0*2-1+1*2-2=8+2+1+¼=11 ¼.

двоичную (N10 ?N2)
Способ – деление на основание системы счисления

?N2) (умножением на 2)
Пример: 0,562510 = N2 = 0,10012
Задание

10: переведите десятичные дроби в двоичную систему счисления с точностью до 6 знаков после запятой:
0,710 0,462210 0,519810 0,580310

двоичную
Алгоритм перевода:
1) перевести целую часть;
2) перевести дробную часть;
3) сложить

полученные результаты.
Пример :перевести 17,2510 в двоичную систему счисления.
Решение:
1710 = 100012
0,2510= 0,012
17,2510 = 10001,012

Задание 11: переведите в двоичную систему счисления числа: 40,510

десятичное число 12 записывается как

110. Найдите это основание.

Решение.
Сначала распишем число 110 через формулу записи чисел в позиционных системах счисления для нахождения значения в десятичной системе счисления, а затем найдем основание методом перебора.




Значит основание системы счисления равно 3.
Ответ. Искомое основание системы счисления равно 3.