- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение сложных задач
Содержание
- 2. При решении заданий С3 обязательным условием является
- 3. Рассмотрим задачу:Два игрока играют в игру. На
- 4. Помним о том, что выигрывает игрок, после
- 8. Вывод:Выиграет второй игрок при любом ходе первого
- 9. Пример 1Пример 2
- 10. Два игрока играют в «Верёвку». Игроки ходят
- 11. Даны две горки фишек, содержащих соответственно 3
- 12. Спасибо за внимание!
- 13. Скачать презентацию
- 14. Похожие презентации
При решении заданий С3 обязательным условием является создание дерева решений, а также умение сделать правильный вывод по полученным результатам.








Слайд 3
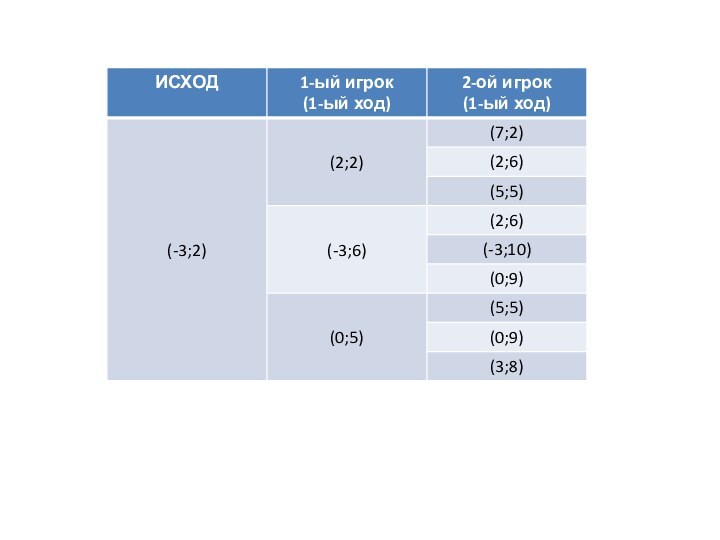
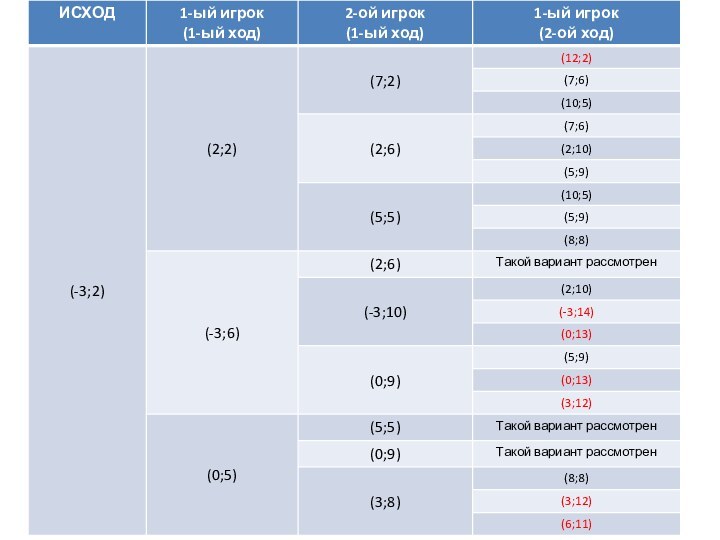
Рассмотрим задачу:
Два игрока играют в игру. На координатной
плоскости в точке с координатами (-3;2) стоит фишка, игроки
ходят по очереди. Ход состоит в том, что игрок перемещает фишку в одну из точек (х+5;у), (х;у+4), (х+3;у+3). Выигрывает игрок, после хода которого расстояние по прямой от фишки до начала координат больше 12. Кто выигрывает при безошибочной игре обоих игроков, игрок делающий первый шаг или игрок, делающий второй ход. Каким должен быть первый ход выигрышного игрокаСлайд 4 Помним о том, что выигрывает игрок, после хода
которого расстояние от фишки до начала координат будет больше
12. Для этого вспомним формулу нахождения расстояния по координатам точек, учитывая, что одна из них это начало координат
Слайд 8
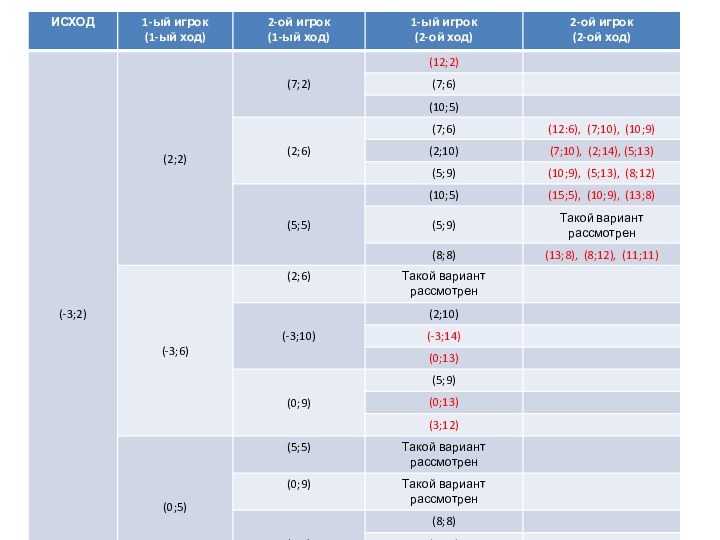
Вывод:
Выиграет второй игрок при любом ходе первого игрока,
если первый ход второго игрока будет (2;6) или (5;5)
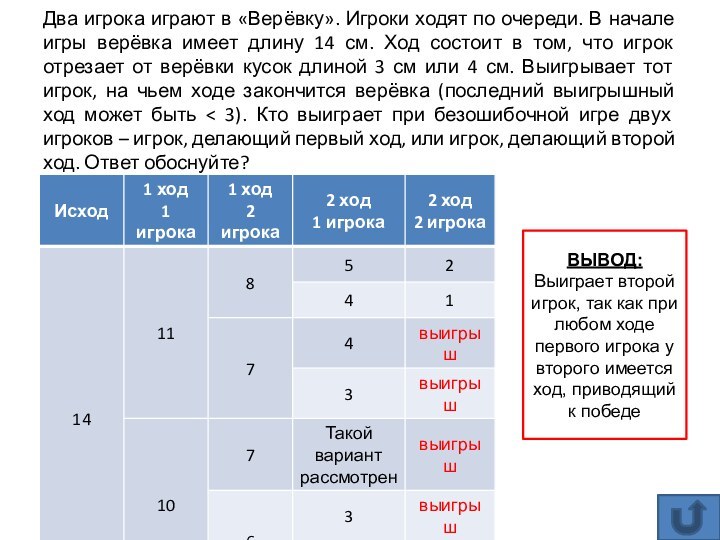
Слайд 10 Два игрока играют в «Верёвку». Игроки ходят по
очереди. В начале игры верёвка имеет длину 14 см.
Ход состоит в том, что игрок отрезает от верёвки кусок длиной 3 см или 4 см. Выигрывает тот игрок, на чьем ходе закончится верёвка (последний выигрышный ход может быть < 3). Кто выиграет при безошибочной игре двух игроков – игрок, делающий первый ход, или игрок, делающий второй ход. Ответ обоснуйте?ВЫВОД:
Выиграет второй игрок, так как при любом ходе первого игрока у второго имеется ход, приводящий к победе
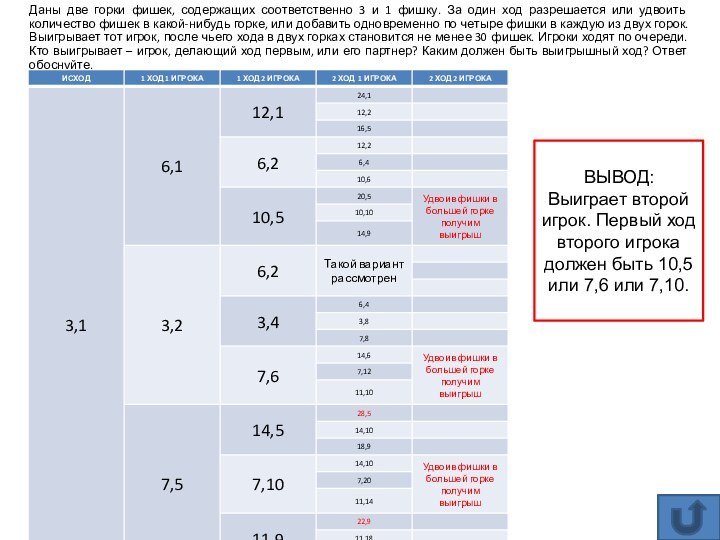
Слайд 11 Даны две горки фишек, содержащих соответственно 3 и
1 фишку. За один ход разрешается или удвоить количество
фишек в какой-нибудь горке, или добавить одновременно по четыре фишки в каждую из двух горок. Выигрывает тот игрок, после чьего хода в двух горках становится не менее 30 фишек. Игроки ходят по очереди. Кто выигрывает – игрок, делающий ход первым, или его партнер? Каким должен быть выигрышный ход? Ответ обоснуйте.ВЫВОД:
Выиграет второй игрок. Первый ход второго игрока должен быть 10,5 или 7,6 или 7,10.