Слайд 2
Линейные списки (однонаправленные цепочки)
Списком называется структура данных, каждый
элемент которой посредством указателя связывается со следующим элементом.
Каждый элемент
связанного списка
хранит какую-либо информацию,
указывает на следующий за ним элемент.
Так как элемент списка хранит разнотипные части (хранимая информация и указатель), то его естественно представить записью, в которой в одном поле располагается объект, а в другом – указатель на следующую запись такого же типа. Такая запись называется звеном, а структура из таких записей называется списком или цепочкой.
Слайд 3
Лишь на самый первый элемент списка (голову) имеется
отдельный указатель. Последний элемент списка никуда не указывает.
Слайд 4
Для иллюстрации работы с линейными списками рассмотрим задачу:
Разработайте
программу работы с односвязным списком. Программа должна содержать следующие
процедуры, вызываемые из меню:
Добавление нового элемента в начало списка.
Добавление нового элемента в конец списка.
Удаление первого элемента.
Вывод списка на экран.
Слайд 5
Описание списка
Пример описания списка
type ukaz=^spisok;
spisok=record
inf:integer;
next:ukaz;
end;
В Паскале существует основное правило: перед использованием какого-либо объекта он должен быть описан. Исключение сделано лишь для указателей, которые могут ссылаться на еще не объявленный тип.
var
ug:ukaz;
a:integer;
Слайд 6
Разработаем программу методом пошаговой детализации.
Чтобы список существовал, надо
определить указатель на его начало.
Создадим список:
begin
new(ug);
ug^.next:=nil;
Выведем названия пунктов меню
соответствующих операциям работы со списками:
writeln('1. Dobavit element v nachalo');
writeln('2. Dobavit element v konets');
writeln('3. udalit 1 element');
writeln('4. exit');
Слайд 7
Организуем бесконечный цикл, и в зависимости от выбранного
пользователем пункта меню будем вызывать соответствующие процедуры.
while true do
begin
writeln('viberite hunkt menu');
readln(a);
case a of
1: begin
writeln('Vvedite element'); readln(a);
dobavlenieVgol(ug,a); vivod(ug);
end;
2: begin
writeln('Vvedite element'); readln(a);
dobavlenieVxvost(ug,a); vivod(ug);
end;
udalenie1(ug); vivod(ug);
end;
4: halt;
else writeln('Net punkta')
end;
end;
end.
Теперь детализируем каждую из процедур:
Слайд 9
А) Добавим элемент в голову списка. Для этого
необходимо выполнить последовательность действий:
получить память для нового элемента;
поместить туда
информацию;
присоединить элемент к голове списка.
procedure dobavlenieVgol(var ug:ukaz; z:integer);
var x:ukaz;
begin
new(x); {Выделяем память для нового элемента }
x^.inf:=z; {Помещаем информацию в поле inf типа integer}
x^.next:=ug^.next; {В поле next типа указатель помещаем тот адрес на который раньше ссылалась голова списка – адрес первого элемента}
ug^.next:=x; {Указатель головы списка переводим на новый элемент}
end;
Слайд 10
Б)Добавление элемента в конец списка. Для этого необходимо
выполнить последовательность действий:
Найти последний элемент списка.
Выделить память для нового
элемента.
Поместить туда информацию.
Присоединить элемент к хвосту списка.
procedure dobavlenieVxvost(ug:ukaz; z:integer);
var x,y:ukaz;
Begin
x:=ug; {Копируем указатель на голову в переменную x}
while x^.next<>nil do x:=x^.next; {Пока просматриваемый элемент полем next не указывает на «пусто» (пока не достигнут конец списка) переходим к следующему элементу}
Слайд 11
new(y); {Выделяем память для нового элемента}
y^.inf:=z;
{Помещаем информацию в поле inf }
y^.next:=nil; {Следующего за
новым элементом не будет, т.к. добавляем в хвост}
x^.next:=y; {Указатель последнего элемента списка переводим на новый элемент}
end;
Слайд 12
Вывод списка на экран
procedure vivod( ug:ukaz);
var x:ukaz;
begin
x:=ug^.next; {Копируем указатель на голову в переменную x}
write('spisok
');
if ug^.next=nil then {Если голова списка указывает на «пусто»}
writeln('pust')
else {Если голова списка не указывает на «пусто»}
Слайд 13
while xnil do {Выполняем цикл до тех
пор, пока x не указывает на «пусто» (пока не
дошли до конца списка)}
begin
write(x^.inf, ' '); {Выводим информацию из поля inf на экран}
x:=x^.next; {Переходим к следующему элементу}
end;
end;
Слайд 14
Удаление первого элемента из списка
Во вспомогательном указателе запомним
указатель на первый элемент.
Поле next указателя на голову переключим
на второй (следующий за первым) элемент списка.
Освободим область динамической памяти, на которую указывает вспомогательный указатель.
procedure udalenie1(var ug:ukaz);
var x:ukaz;
begin
if ug^.next=nil then
begin
writeln('Spisok pust');
end
Слайд 15
else
begin
x:=ug^.next; {Во вспомогательном указателе запомним
адрес первого элемента}
ug^.next:=x^.next; {Поле next указателя
на голову переключим на второй (следующий за первым) элемент списка}
dispose(x); {Освободим область динамической памяти, на которую указывает вспомогательный указатель}
end;
end;
Слайд 16
Продемонстрируем применение вышеприведенных процедур в итоговой программе:
type ukaz=^spisok;
spisok=record
inf:integer;
next:ukaz;
end;
var
ug:ukaz;
a:integer;
procedure udalenie1(var ug:ukaz);
var x:ukaz;
begin
if ug^.next=nil then
Слайд 17
begin
writeln('Spisok pust');
exit;
end
else
begin
x:=ug^.next;
ug^.next:=x^.next;
dispose(x);
end;
end;
procedure vivod( ug:ukaz);
Слайд 18
var x:ukaz;
begin
x:=ug^.next;
write('spisok ');
if ug^.next=nil then
writeln('pust')
else
while xnil do
begin
write(x^.inf, ' ');
x:=x^.next;
end;
end;
Слайд 19
procedure dobavlenieVxvost(ug:ukaz; z:integer);
var x,y:ukaz;
begin
x:=ug;
while x^.nextnil
do
x:=x^.next;
new(y);
y^.inf:=z;
y^.next:=nil;
x^.next:=y;
end;
Слайд 20
procedure dobavlenieVgol(var ug:ukaz; z:integer);
var x:ukaz;
begin
new(x);
x^.inf:=z;
x^.next:=ug^.next;
ug^.next:=x;
end;
begin
new(ug);
ug^.next:=nil;
Слайд 21
writeln('1. Dobavit element v nachalo');
writeln('2. Dobavit
element v konets');
writeln('3. udalit 1 element');
writeln('4. exit');
while true do
begin
writeln('viberite hunkt menu');
readln(a);
case a of
1: begin
writeln('Vvedite element'); readln(a);
dobavlenieVgol(ug,a); vivod(ug);
end;
writeln('Vvedite element'); readln(a);
dobavlenieVxvost(ug,a); vivod(ug);
end;
3: begin
udalenie1(ug); vivod(ug);
end;
4: halt;
else writeln('Net punkta')
end;
end;
end.
Слайд 23
Двунаправленный список
Использование однонаправленных списков при решении ряда задач
может вызвать определенные трудности.
По однонаправленному списку можно двигаться
только в одном направлении, от головы списка к последнему звену. Между тем нередко возникает необходимость произвести какую-либо операцию с элементом, предшествующим элементу с заданным свойством. Однако после нахождения элемента с данным свойством в однонаправленном списке у нас нет возможности получить удобный и быстрый способ доступа к предыдущему элементу.
Для устранения этого неудобства добавим в каждое звено списка еще одно поле, значением которого будет ссылка на предыдущее звено.
Слайд 24
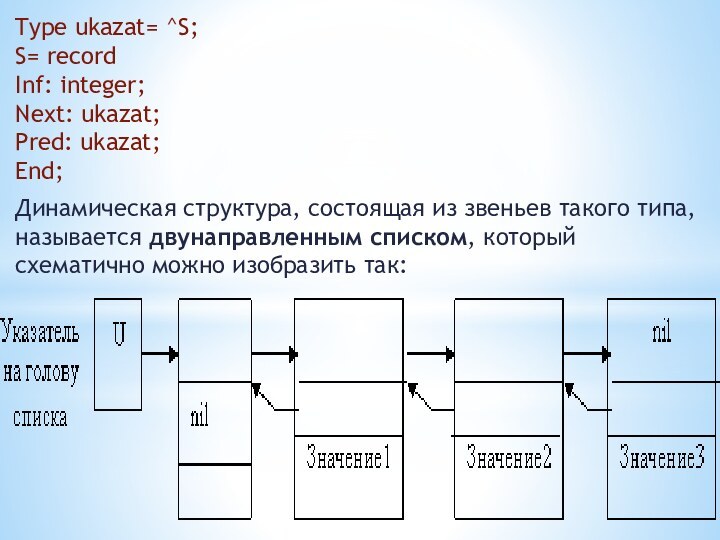
Type ukazat= ^S;
S= record
Inf: integer;
Next:
ukazat;
Pred: ukazat;
End;
Динамическая структура, состоящая из звеньев
такого типа, называется двунаправленным списком, который схематично можно изобразить так:
Слайд 25
Наличие в каждом звене двунаправленного списка ссылки как
на следующее, так и на предыдущее звено позволяет от
каждого звена двигаться по списку в любом направлении. По аналогии с однонаправленным списком здесь есть заглавное звено. В поле Pred этого звена фигурирует пустая ссылка nil, свидетельствующая, что у заглавного звена нет предыдущего (так же, как у последнего нет следующего).
Слайд 26
Кольцевые списки
В программировании двунаправленные списки часто обобщают следующим
образом: в качестве значения поля Next последнего звена принимают
ссылку на заглавное звено, а в качестве значения поля Pred заглавного звена – ссылку на последнее звено:
Слайд 27
Как видно, здесь список замыкается в своеобразное «кольцо»:
двигаясь по ссылкам, можно от последнего звена переходить к
заглавному звену, а при движении в обратном направлении – от заглавного звена переходить к последнему. Списки подобного рода называют кольцевыми списками.
Кольцевые списки бывают однонаправленными и двунаправленными.
Слайд 28
Стек и очередь
Стек –вид списка, обращение к которому
идет только через указатель на первый элемент. Если в
стек нужно добавить элемент, то он добавляется впереди первого элемента, при этом указатель на начало стека переключается на новый элемент. Алгоритм работы со стеком характеризуется правилом: «последним пришел – первым вышел».
Очередь – это вид списка, имеющего два указателя на первый и последний элемент цепочки. Новые элементы записываются вслед за последним, а выборка элементов идет с первого. Этот алгоритм типа «первым пришел – первым вышел».
Возможно организовать списки с произвольным доступом к элементам. В этом случае необходим дополнительный указатель на текущий элемент.
Слайд 29
Деревья
Дерево – это совокупность элементов, называемых узлами (один
из которых определен как корень), и отношений, образующих иерархическую
структуру узлов.
Формально дерево определяется как конечное множество T одного или более узлов со следующими свойствами:
Существует один выделенный узел, а именно – корень данного дерева;
Остальные узлы (за исключением корня) распределены среди m непересекающихся множеств T1 , T2 , …. Tm , и каждое из этих множеств, в свою очередь, является деревом; деревья T1 , T2 , ... Tm называются поддеревьями данного корня.
Слайд 30
Т.е. каждый узел дерева является корнем некоторого поддерева
данного дерева.
Количество поддеревьев узла называется степенью этого узла.
Узел с нулевой степенью называется концевым узлом или листом.
Каждый узел имеет уровень, который определяется следующим образом: уровень корня дерева равен нулю, а уровень любого другого узла на единицу выше, чем уровень корня ближайшего поддерева, содержащего данный узел.
Слайд 31
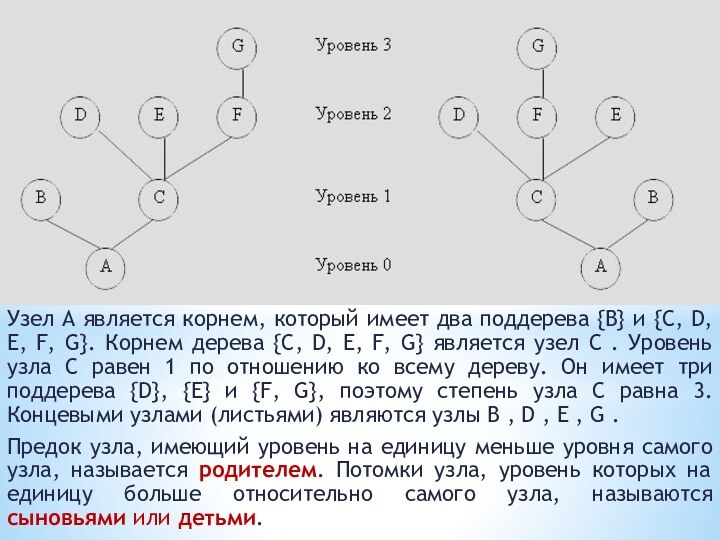
Узел A является корнем, который имеет два поддерева
{B} и {C, D, E, F, G}. Корнем дерева
{C, D, E, F, G} является узел C . Уровень узла C равен 1 по отношению ко всему дереву. Он имеет три поддерева {D}, {E} и {F, G}, поэтому степень узла C равна 3. Концевыми узлами (листьями) являются узлы B , D , E , G .
Предок узла, имеющий уровень на единицу меньше уровня самого узла, называется родителем. Потомки узла, уровень которых на единицу больше относительно самого узла, называются сыновьями или детьми.
Слайд 32
Обходы дерева
Существует несколько способов обхода всех узлов дерева.
Три наиболее часто используемых способа обхода называются прямой, обратный
и симметричный обходы. Все три способа можно рекурсивно определить следующим образом:
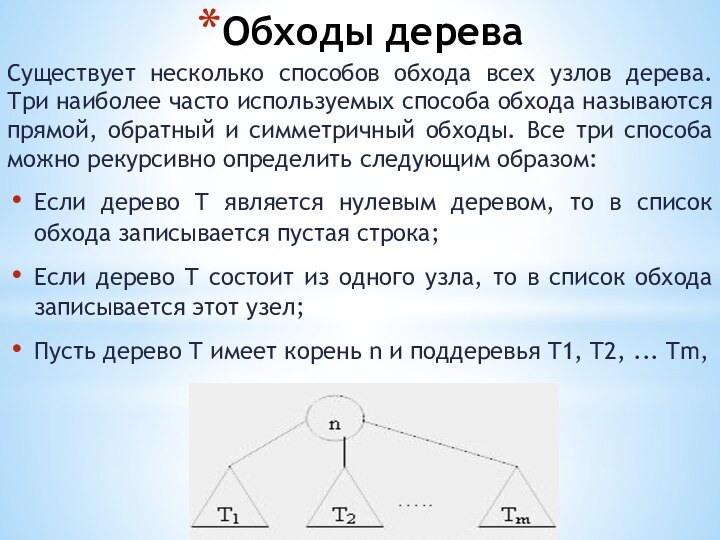
Если дерево T является нулевым деревом, то в список обхода записывается пустая строка;
Если дерево T состоит из одного узла, то в список обхода записывается этот узел;
Пусть дерево T имеет корень n и поддеревья T1, T2, ... Tm,
Слайд 33
Прямой обход. Сначала посещается корень n , затем
в прямом порядке узлы поддерева T1, далее все узлы
поддерева T2 и т.д. Последними посещаются в прямом порядке узлы поддерева Tm .
Обратный обход. Сначала посещаются в обратном порядке все узлы поддерева T1, затем в обратном порядке узлы поддеревьев T2 … Tm, последним посещается корень n .
Симметричный обход. Сначала в симметричном порядке посещаются все узлы поддерева T1 , затем корень n , после чего в симметричном порядке все узлы поддеревьев T2 … Tm .
Слайд 34
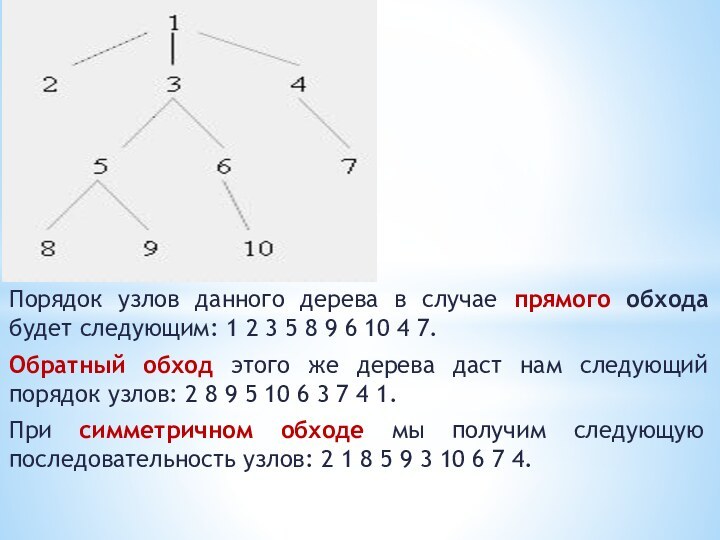
Порядок узлов данного дерева в случае прямого обхода
будет следующим: 1 2 3 5 8 9 6
10 4 7.
Обратный обход этого же дерева даст нам следующий порядок узлов: 2 8 9 5 10 6 3 7 4 1.
При симметричном обходе мы получим следующую последовательность узлов: 2 1 8 5 9 3 10 6 7 4.
Слайд 35
Двоичные деревья
Двоичное или бинарное дерево – это наиболее
важный тип деревьев. Каждый узел бинарного дерева имеет не
более двух поддеревьев, причем в случае только одного поддерева следует различать левое или правое.
Бинарное дерево – это конечное множество узлов, которое является либо пустым, либо состоит из корня и двух непересекающихся бинарных деревьев, которые называются левым и правым поддеревьями данного корня.
Бинарное дерево можно представить в виде динамической структуры данных, состоящей из узлов, каждый из которых содержит кроме данных не более двух ссылок на правое и левое бинарное дерево. На каждый узел имеется одна ссылка. Начальный узел называется корнем.
Слайд 36
По аналогии с элементами списков, узлы дерева удобно
представить в виде записей, хранящих информацию и два указателя:
Пример
type ptree=^tree;
tree=record
inf:integer;
left,right:ptree;
end;
Слайд 37
Дерево поиска
Способ построения дерева, при котором для каждого
узла все ключи (значения узлов) его левого поддерева меньше
ключа этого узла, а все ключи его правого поддерева больше, называется деревом поиска или двоичным упорядоченным деревом.
С помощью дерева поиска можно организовать эффективный способ поиска, который значительно эффективнее поиска по списку.
Поиск в дереве поиска выполняется по следующему рекурсивному алгоритму:
Если дерево не пусто, то нужно сравнить искомый ключ с ключом в корне дерева:
- если ключи совпадают, поиск завершен;
- если ключ в корне больше искомого, выполнить поиск в левом поддереве;
- если ключ в корне меньше искомого, выполнить поиск в правом поддереве.
Если дерево пусто, то искомый элемент не найден.
Слайд 38
Дерево поиска может быть использовано для построения упорядоченной
последовательности ключей узлов. Например, если мы используем симметричный порядок
обхода такого дерева, то получим упорядоченную по возрастанию последовательность.
Можно организовать «зеркально симметричный» обход, начиная с правого поддерева, тогда получим упорядоченную по убыванию последовательность.
Таким образом, деревья поиска можно применять для сортировки значений.
Слайд 39
Разработайте программу работы с бинарным деревом. Программа должна
содержать следующие процедуры, вызываемые из меню:
построение пустого дерева;
добавление нового
элемента;
просмотр дерева в симметричном порядке: левая ветвь, узел, правая ветвь;
поиск элемента;
удаление элемента.
Слайд 40
Создание пустого дерева
type ptree=^tree;
tree=record
inf:integer;
left,right:ptree;
end;
procedure sozdanie(var kor:ptree);
begin
new(kor);
kor:=nil;
end;
Слайд 41
Добавление элемента
Для того чтобы вставить узел, необходимо найти
его место. Для этого мы сравниваем вставляемое значение с
корнем, если оно больше, чем значение корня, уходим в правое поддерево, а иначе – в левое. Тем же образом продвигаемся дальше, пока не дойдем до конечного узла (листа). Сравниваем вставляемое значение со значением листа. Если оно меньше, то добавляем листу левого сына, а иначе – правого сына.
procedure (var kor:ptree; z:integer);
begin
if kor=nil then {Если дерево пустое, то добавляемый элемент станет корнем}
begin
new(p); {Выделяем память для нового элемента}
Слайд 42
p^.inf:=z; {Записываем в поле inf информацию}
p^.left:=nil;{Левые и правые сыновья нового элемента nil}
p^.right:=nil; {т.к. в дерево можно добавлять только лист}
kor:=p
end
else {Если дерево не пустое}
begin
if z begin { Если вставляемое значение меньше значения корня}
if kor^.left=nil then {и у корня нет левого сына, то добавим новое значение левым сыном корня}
p^.inf:=z;
p^.left:=nil;
p^.right:=nil;
kor^.left:=p
end
else {если у корня есть левый сын, то вызываем процедуру добавления (рекурсия) для левого сына (т.е. теперь левый сын рассматривается как корень)}
begin
Dobavl(kor^.left, z);
end;
kor^.right=nil then {если вставляемое значение не меньше корня, то,
если у корня нет правого сына, то добавляем новое значение в качестве правого сына корня}
begin
new(p);
p^.inf:=z;
p^.left:=nil;
p^.right:=nil;
kor^.right:=p
end
else dobavl(kor^.right, z); {если у корня есть правый сын, то вызываем процедуру добавления (рекурсия) для правого сына (т.е. теперь правый сын рассматривается как корень)}
end; {Заканчиваем случай, когда дерево не пустое}
end;
Слайд 45
Обход дерева и вывод на экран (левая ветвь,
корень, правая ветвь)
procedure vivod(kor:ptree);
begin
if
kor^.left<>nil then vivod(kor^.left); {Если у узла kor есть левый сын, то вызываем процедуру вывод для левого сына вершины kor}
writeln(kor^.inf); {Выводим информацию узла kor}
if kor^.right<>nil then vivod(kor^.right); {Если у узла kor есть правый сын, то вызываем процедуру вывод для правого сына вершины kor}
end;
Слайд 46
Поиск узла с заданным значением
Функция poisk не только
возвращает значение true, если в дереве есть искомый элемент
со значением z, и false, если такого элемента нет, но и находит указатели на этот элемент (p) и на его предка (parent), они передаются в качестве параметров-переменных.
function poisk(kor:ptree; z:integer; var p,parent:ptree):boolean;
begin
P:=kor; {Начинаем поиск с корня}
parent:=nil;
while p<>nil do {Пока мы не «выйдем за границы дерева»}
begin
if z=p^.inf then {Если узел p имеет искомое значение z}
begin {Элемент найден, выходим из процедуры}
poisk:=true; exit;
end;
Слайд 47
parent:=p; {текущее значение указателя p сохраняем в
переменной parent как предка}
if z
p:=p^.left {Если искомое значение z меньше информации в текущем узле p, то рассмотреть в качестве p его левого сына (спуститься влево)}
else p:=p^.right; {Если искомое значение z больше информации в текущем узле p, то рассмотреть в качестве p его правого сына (спуститься вправо)}
end; {Конец цикла, пока не «выйдем за границы дерева»}
poisk:=false; {Если мы не нашли элемента с искомым значением z, то его в дереве нет}
end;
Слайд 48
Удаление узла
Если узел является конечным (то есть не
имеет потомков), то его удаление не вызывает трудностей, достаточно
обнулить соответствующий указатель узла-родителя (сделать его ссылку равной nil).
Слайд 49
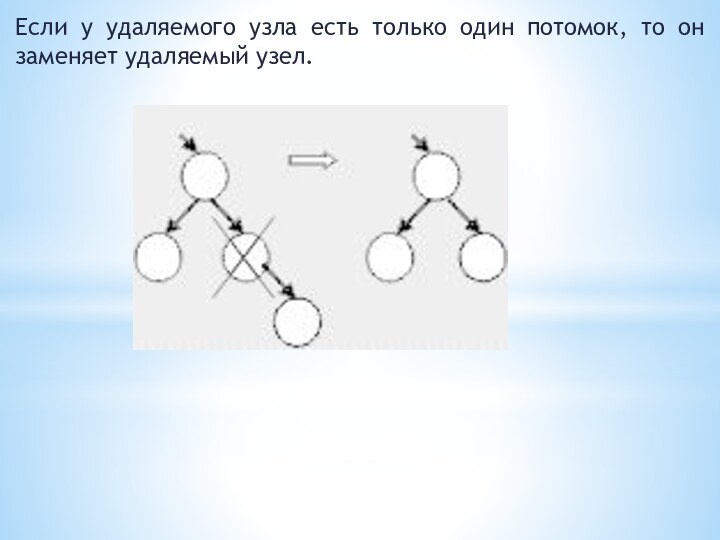
Если у удаляемого узла есть только один потомок,
то он заменяет удаляемый узел.
Слайд 50
Сложнее всего случай, когда у удаляемого узла есть
оба потомка.
Есть простой особый случай: если у правого
потомка удаляемого узла нет левого потомка, удаляемый узел заменяется на своего правого потомка, а левый потомок удаляемого узла подключается вместо отсутствующего левого потомка к замещающему узлу.
Слайд 51
В общем же случае на место удаляемого узла
ставится самый левый узел его правого поддерева (или наоборот
– самый правый узел его левого поддерева). Это не нарушает свойств дерева поиска.
Слайд 52
procedure del(var kor:ptree; z:integer); {Удаляет узел со значением
z из дерева с корнем kor}
var
p:ptree;
{указатель, в котором будет храниться адрес удаляемого элемента}
parent:ptree; {указатель, в котором будет храниться адрес предка удаляемого элемента (чтобы знать к кому подключать замещающий элемент)}
y:ptree; {указатель, в котором будет храниться адрес замещающего элемента}
Для процедуры удаления нам понадобится вспомогательная функция findZamena, которая возвращает указатель на узел, замещающий удаляемый, кроме этого в ней осуществляются все необходимые действия по переподключению узлов, чтобы дерево сохранило свойства дерева поиска. В нее передается указатель на удаляемый узел p.
Слайд 53
function findZamena(p:ptree):ptree;
var
y:ptree; {Указатель на
узел, замещающий удаляемый}
predy:ptree; {Указатель на предка узла,
замещающего удаляемый}
begin
if p^.left=nil then y:=p^.right {Если у удаляемого узла нет левого потомка, то замещающим станет правый потомок удаляемого узла}
else if p^.right=nil then y:=p^.left {Если у удаляемого узла есть левый потомок, но нет правого потомка, то замещающим станет левый потомок удаляемого узла}
else {Если у удаляемого узла есть оба потомка}
begin
y:=p^.right; {Указатель на узел, замещающий удаляемый, переводим на правого сына удаляемого узла
( переходим в правое поддерево)}
Слайд 54
if y^.left=nil then y^.left:=p^.left {Если у правого
сына удаляемого узла (на него указывает y) нет левого
сына, то наш поиск окончен (удаляемый узел заменяется на своего правого потомка, а именно на него указывает y), необходимо только левого потомка удаляемого узла p подключить к замещающему узлу y вместо отсутствующего левого потомка}
else {Если у правого сына удаляемого узла есть левый сын}
begin
repeat
predy:=y; {Текущее значение указателя y сохраняем в качестве указателя на предка y}
y:=y^.left; {А указатель у переводим на его левого сына (идем по самой левой ветке, чтобы найти самый левый узел его правого поддерева)}
until y^.left<>nil; {Действия повторяем до тех пор, пока не дойдем до узла у которого нет левого сына, он и должен заменить удаляемый узел}
Слайд 55
y^.left:=p^.left;
{Подключаем к узлу y, замещающему удаляемый узел p, левого
потомка удаляемого узла (своего левого у него нет)}
predy^.left:=y^.right; {Правого сына замещающего узла y подключаем в качестве левого сына к предку y (на то место, где раньше был y)}
y^.right:=p^.right; {Правого сына удаляемого узла p подключаем в качестве правого сына к замещающему узлу y }
end;
end;
findZamena:=y; {Имени функции присваиваем результат}
end; {Конец процедуры findZamena}
Слайд 56
begin {начало самой процедуры удаления del }
{При вызове
процедуры poisk, которая возвращает значение булевского типа, в переменной
p возвращается указатель на удаляемый элемент, а в переменной parent указатель на его предка}
if not poisk(kor, z, p, parent) then {Если в дереве с корнем kor не найден удаляемый элемент z}
begin
writeln('net elementa'); {Выводим соответствующее сообщение}
exit; {И выходим из процедуры}
end;
y:=findZamena(p); {у присваиваем указатель на элемент, замещающий удаляемый элемент p, и производим все необходимые переподключения узлов, чтобы наше дерево сохранило свойства дерева поиска}
Слайд 57
if p=kor then kor:=y {Если удаляемый элемент
является корнем дерева, надо указателю на корень присвоить указатель
на замещающий элемент y}
else {иначе – присоединить этот указатель к соответствующему поддереву предка parent удаляемого узла}
if z
else parent^.right:=y; {В противном случае удаляемый узел был правым сыном parent и мы подключаем замещающий узел y в качестве правого сына}
dispose(p); {Освобождаем память, занимаемую указателем p}
end; {Конец процедуры del}
Слайд 58
Вся программа:
Разработайте программу работы с бинарным деревом. Программа
должна содержать следующие процедуры, вызываемые из меню:
построение пустого дерева;
добавление
нового элемента;
просмотр дерева в следующем порядке: левая ветвь, узел, правая ветвь;
поиск элемента;
удаление элемента.
Слайд 59
Type
ptree=^tree;
tree=record
inf:integer;
left,right:ptree;
end;
Var
p,kor,parent:ptree;
a, z:integer;
Слайд 60
procedure Sozdanie(var kor:ptree);
begin
new(kor);
kor:=nil;
end;
procedure Dobavl(var kor:ptree; z:integer);
begin
if kor=nil then
begin
new(p);
p^.inf:=z;
p^.left:=nil;
p^.right:=nil;
Слайд 61
kor:=p;
end
else
begin
if z
begin
if kor^.left=nil then
begin
new(p);
p^.inf:=z;
p^.left:=nil;
p^.right:=nil;
kor^.left:=p
end
Слайд 62
else
begin
Dobavl(kor^.left, z);
end;
end
else
if
kor^.right=nil then
begin
new(p);
p^.inf:=z;
p^.left:=nil;
p^.right:=nil;
kor^.right:=p
end
Слайд 63
else Dobavl(kor^.right, z);
end;
end;
Слайд 64
procedure Vivod(kor:ptree);
begin
if kor^.leftnil then
Vivod(kor^.left);
Writeln(kor^.inf);
if kor^.rightnil then
Vivod(kor^.right);
end;
function Poisk(kor:ptree; z:integer; var p,parent:ptree):boolean;
begin
P:=kor;
while p<>nil do
begin
Слайд 65
if z=p^.inf then
begin
poisk:=true;
exit;
end;
parent:=p;
if z
p:=p^.left
else
p:=p^.right;
end;
poisk:=false;
end;
Слайд 66
procedure del(var kor:ptree; z:integer);
var
p:ptree; {udaljaemij el}
parent:ptree;
{predok p}
y:ptree; {zamenit p}
function findZamena(p:ptree):ptree;
var
y:ptree; {zamena
p}
predy:ptree; {predok y}
begin
if p^.left=nil then y:=p^.right
else
if p^.right=nil then y:=p^.left
else
Слайд 67
begin
y:=p^.right;
if y^.left=nil then
y^.left:=p^.left
else
begin
repeat
predy:=y;
y:=y^.left;
until
y^.left<>nil;
y^.left:=p^.left;
predy^.left:=y^.right;
y^.right:=p^.right;
end;
end;
findZamena:=y;
end;
Слайд 68
begin
if not poisk(kor, z,p,parent) then
begin
writeln(‘Нет элемента’);
exit;
end;
y:=findZamena(p);
if p=kor then
kor:=y
else
if z
parent^.left:=y
else
parent^.right:=y;
dispose(p);
end;
Слайд 69
Begin
while a6 do
begin
Writeln('1. Sozdanie');
Writeln('2. Dobavlenie elementa');
Writeln('3. Delete');
Writeln('4.
Poisk');
Writeln('5. Vivod');
Writeln('6. Exit');
Readln(a);
case a of
1: begin
Sozdanie(kor);
end;
Слайд 70
2: begin
writeln('Vvedite chislo');
readln(z);
Dobavl(kor, z);
Vivod(kor);
writeln;
end;
3: begin
Write('Vvedite chislo ');
Readln(a);
Del(kor,a);
end;
Слайд 71
4: begin
Write('Vvedite
chislo');
Readln(a);
if Poisk(kor,a,p,parent) then Writeln(‘yes!')
else Writeln(‘no!');
end;
5: begin
Vivod(kor);
end;
6: begin
Halt;
end;
end;
end;
end.