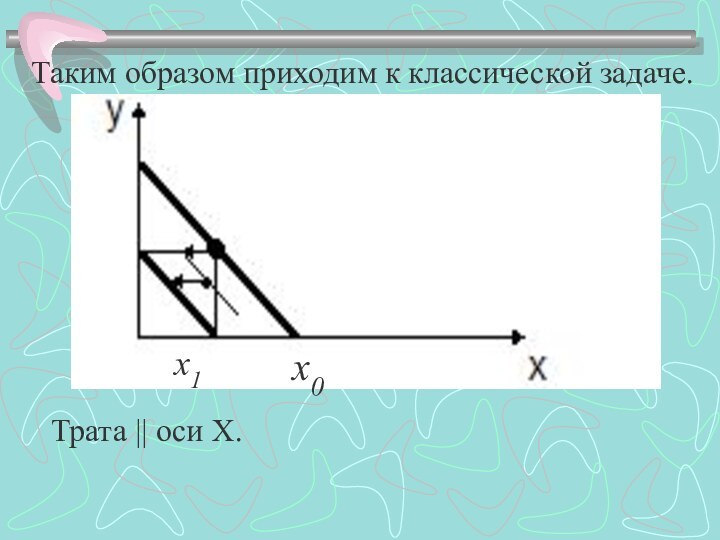
он специально приспособлен для оптимизации динамических задач, в которых
операция состоит из элементов, сильно влияющих друг на друга.ДП связано с именем Ричарда Беллмана, который сформулировал принцип Беллмана. Он позволяет существенно сократить перебор решений в многоэтапных нелинейных задачах.