- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Моделирование статистического прогнозирования. Прогнозирование по регрессионной модели
Содержание
- 2. Вопросы к изучению
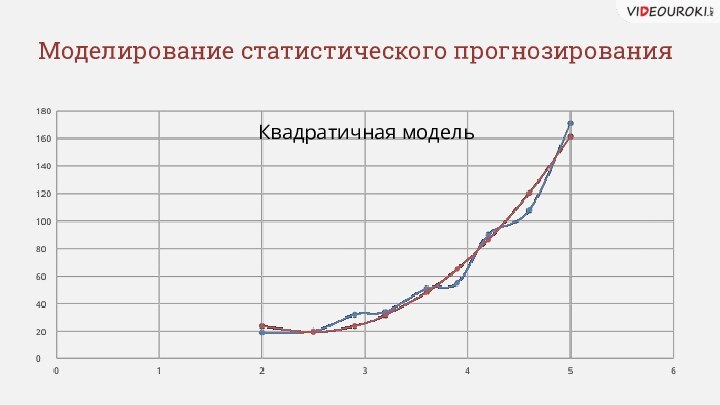
- 3. Моделирование статистического прогнозированияКвадратичная модель
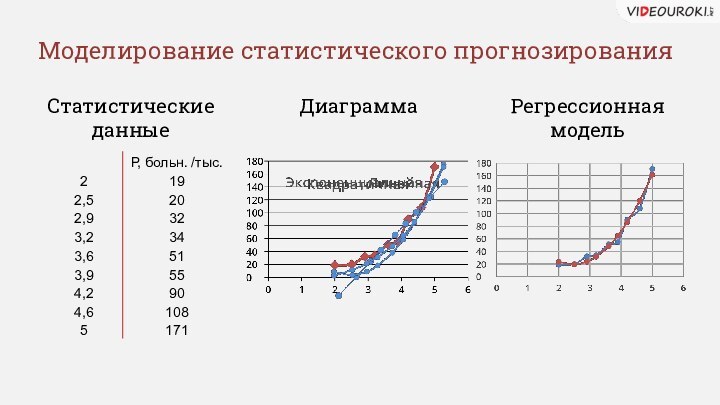
- 4. Моделирование статистического прогнозированияРегрессионная модельСтатистические данныеДиаграмма
- 5. Регрессионная модель – это функция, описывающая зависимость между количественными характеристиками сложных систем.
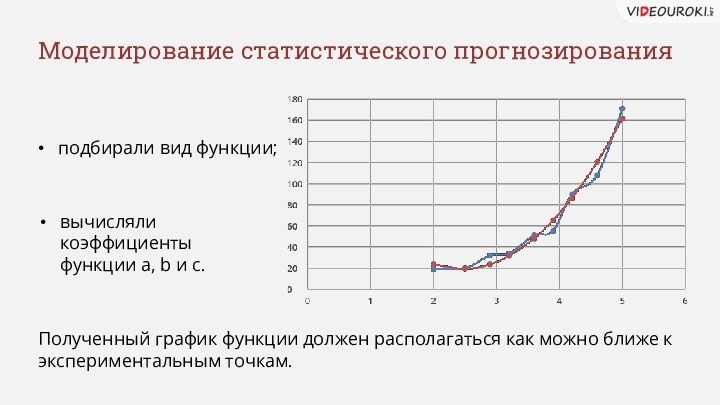
- 6. Моделирование статистического прогнозированияподбирали вид функции;вычисляли коэффициенты функции
- 7. Метод наименьших квадратов
- 8. График регрессионной модели называется трендом.
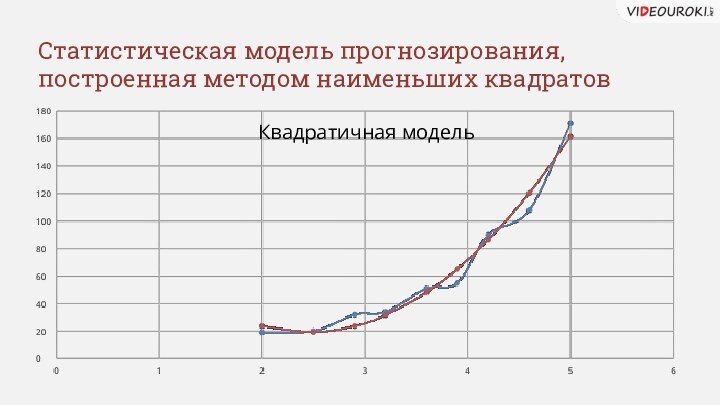
- 9. Статистическая модель прогнозирования, построенная методом наименьших квадратовКвадратичная модель
- 10. В статистике величина R2 называется коэффициентом детерминированности.Показывает, насколько удачной является полученная регрессионная модель.
- 11. Для чего мы выполняли все эти построения и вычисления? Для чего нужны такие модели?
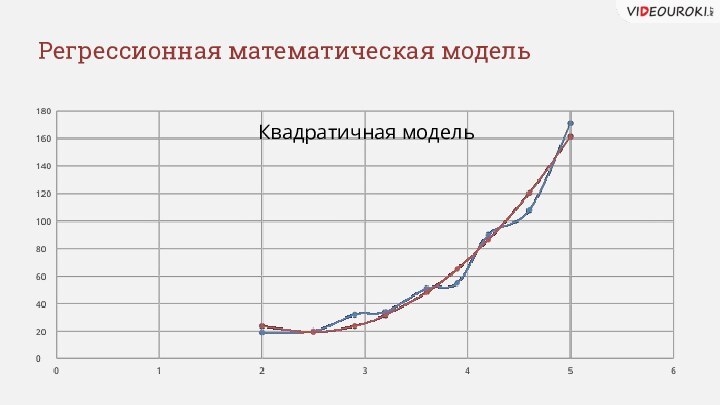
- 12. Регрессионная математическая модельКвадратичная модель
- 13. Модель — это объект-заменитель, который вопределённых условиях
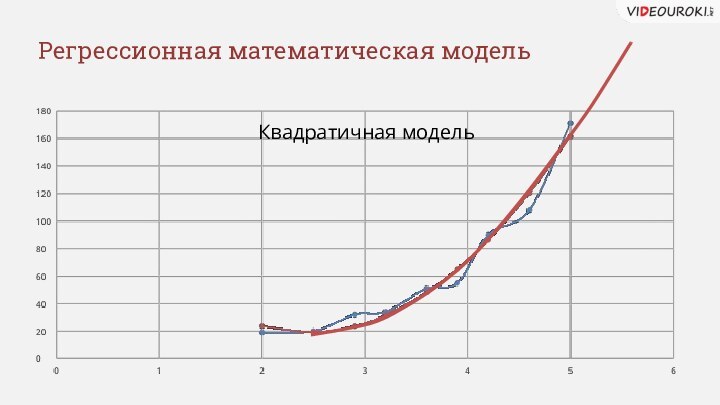
- 14. Регрессионная математическая модельКвадратичная модель
- 16. Способы прогнозирования по регрессионной моделиСпособыВосстановление значения
- 17. Если прогноз рассчитывается в пределах экспериментальных значенийнезависимой переменной, то такой прогнозназывается восстановлением значения.
- 18. Способы прогнозирования по регрессионной моделиСпособыВосстановление значенияЭкстраполяция
- 19. Если прогноз рассчитывается за пределамиэкспериментальных данных, то такойпрогноз называется экстраполяцией.
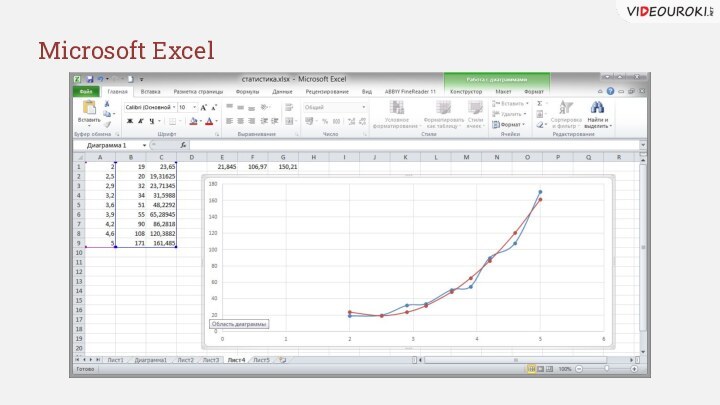
- 20. Microsoft Excel
- 21. Пример
- 22. Восстановление значения
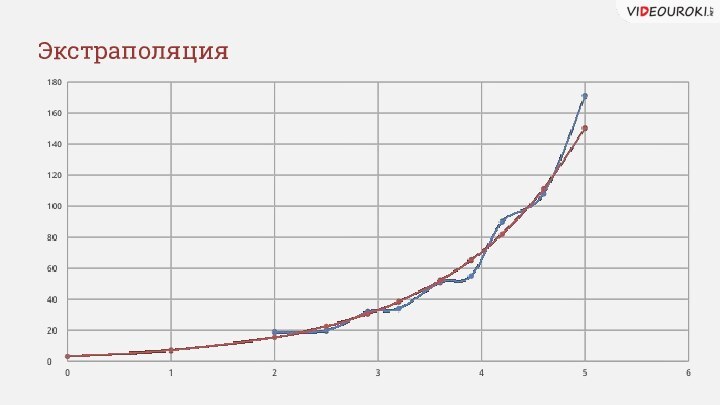
- 23. Экстраполяция
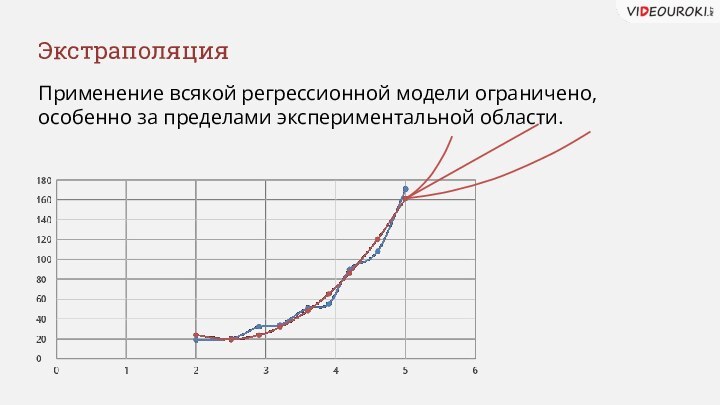
- 24. ЭкстраполяцияПрименение всякой регрессионной модели ограничено, особенно за пределами экспериментальной области.
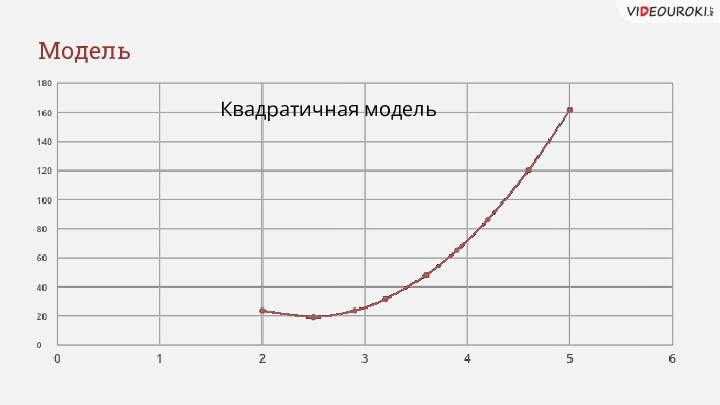
- 25. МодельКвадратичная модель
- 26. Экстраполяция
- 27. Экстраполяция
- 28. Скачать презентацию
- 29. Похожие презентации
Вопросы к изучению