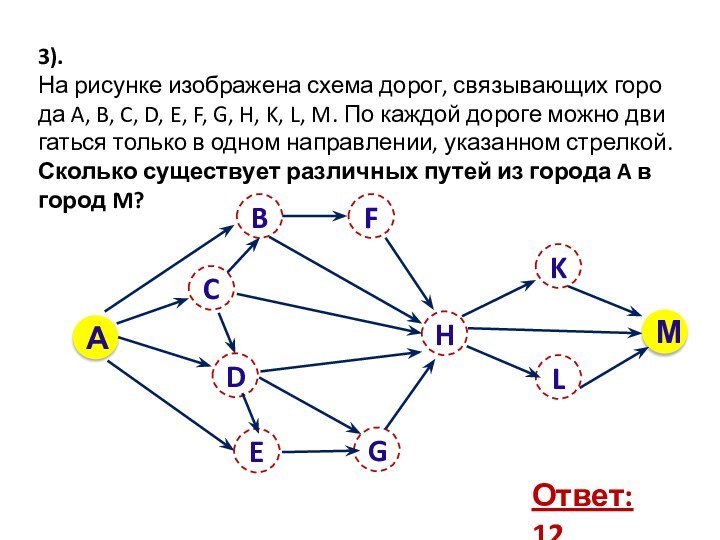
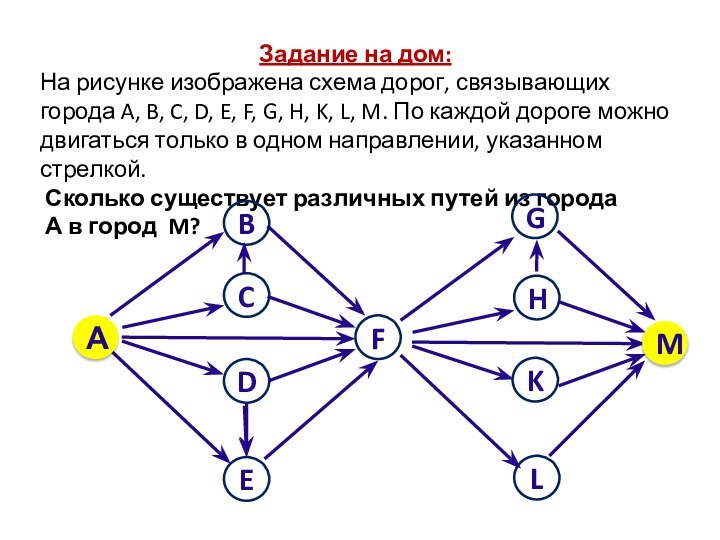
объектов со связями между ними.
Объекты рассматриваются как вершины, или
узлы графа, а связи – как дуги, или ребра.
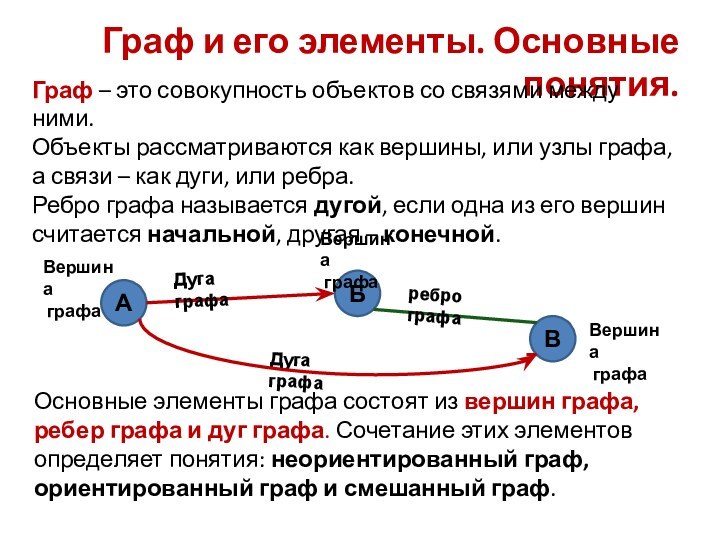
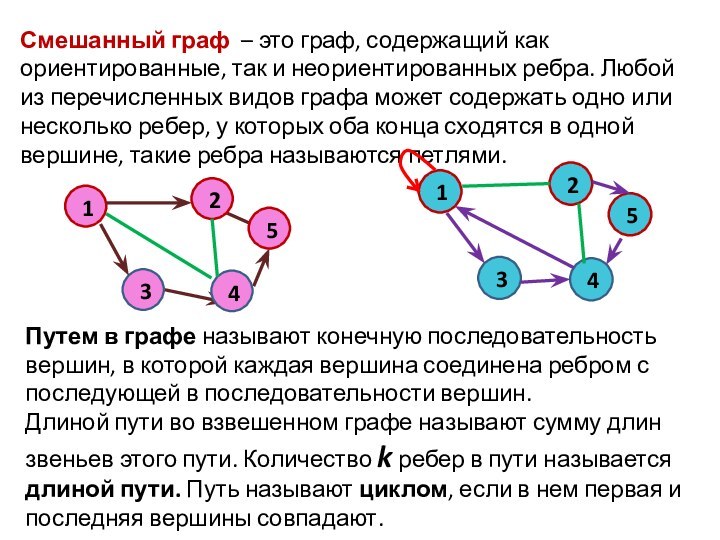
Ребро графа называется дугой, если одна из его вершин считается начальной, другая – конечной.
Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф.
А
Б
В
Дуга графа
Дуга графа
ребро графа
Вершина
графа
Вершина
графа
Вершина
графа