Слайд 2
Понятие «информация» и свойства информации
Измерение информации. Алфавитный подход
Измерение
информации. Содержательный подход
Представление и кодирование информации
Представление числовой информации с
помощью систем счисления
Перевод чисел в позиционных системах счисления
Арифметические операции в позиционных системах счисления
Представление чисел в компьютере
Двоичное кодирование информации
Хранение информации
Слайд 3
Понятие «информация» и свойства информации
Понятие «информация»
Информация в философии
Информация
в физике
Информация в биологии
Свойства информации
Слайд 4
Что такое информация?
Слово «информация» происходит от латинского слова
information, которое переводится как разъяснение, изложение.
Понятие «информация» является фундаментальным
в курсе информатики, невозможно дать его определение через другие, более «простые» понятия.
Слайд 5
В простейшем бытовом понимании с термином «информация» обычно
ассоциируются некоторые сведения, данные, знания. Информация передается в виде
сообщений, определяющих ее форму и представление. Примерами сообщений являются: музыкальное произведение, телепередача, текст, напечатанный на принтере и т.д.
При этом предполагается, что имеются источник информации и получатель информации. Сообщение от источника к получателю передается посредством какой-нибудь среды, являющейся каналом связи.(рис. 1.)
Понятие «информация» используется в различных науках.
Слайд 6
Информация
в
философии
Сообщение ученика
Слайд 7
Информация
в
физике
Сообщение ученика
Слайд 8
Информация
в
биологии
Сообщение ученика
Слайд 9
Свойства информации
Человек – существо социальное, для общения с
другими людьми он должен обмениваться с ними информацией, причем
обмен информацией всегда производится на определенном языке – русском, английском и т.д. участники дискуссии должны владеть тем языком, на котором ведется общение, тогда информация будет понятной всем участникам обмена информацией.
Информация должна быть полезной, тогда дискуссия приобретает практическую ценность. Бесполезная информация создает информационный шум, который затрудняет восприятие полезной информации.
Слайд 10
Широко известен термин «средства массовой информации», которые доводят
информацию до каждого члена общества. Такая информация должна быть
достоверной и актуальной. Недостоверная информация вводит членов общества в заблуждение и может быть причиной возникновения социальных потрясений. Неактуальная информация бесполезна и поэтому никто, кроме историков, не читает прошлогодних газет.
Для того чтобы человек мог правильно ориентироваться в окружающем мире, информация должна быть полной и точной. Задача получения полной и точной информации стоит перед наукой. Овладение научными знаниями в процессе обучения позволяют человеку получить полную и точную информацию о природе, обществе и технике.
Слайд 11
Измерение информации. Алфавитный подход
Алфавитный подход используется для измерения
количества информации в тексте, представленном в виде последовательности символов
некоторого алфавита. Такой подход не связан с содержанием текста. Количество информации в этом случае называется информационным объемом текста, который пропорционален размеру текста – количеству символов, составляющих текст. Иногда данный подход к измерению информации называют объемным подходом.
Слайд 12
Каждый символ текста несет определенное количество информации. Его
называют информационным весом символа. Поэтому информационный объем текста равен
сумме информационных весов всех символов, составляющих текст.
Здесь предполагается, что текст – это последовательная цепочка пронумерованных символов. В формуле (1) i1 обозначает информационный вес первого символа текста, i2 – информационный вес второго символа текста и т.д.; K – размер текста, т.е. полное число символов в тексте
(1)
Слайд 13
Все множество различных символов, используемых для записи текстов,
называется алфавитом. Размер алфавита – целое число, которое называется
мощностью алфавита. Следует иметь в виду, что в алфавит входят не только буквы определенного алфавита, но все другие символы, которые могут использоваться в тексте: цифры, знаки препинания, различные скобки.
Определение информационных весов символов может происходить в двух приближениях:
в предположении равной вероятности (одинаковой частоты встречаемости) любого символа в тексте;
с учетом разной вероятности (разной частоты встречаемости) различных символов в тексте.
Слайд 14
Приближение равной вероятности символов в тексте
Если допустить, что
все символы алфавита в любом тексте появляются с одинаковой
частотой, то информационный вес всех символов будет одинаковым. Тогда доля любого символа в тексте составляет 1/N-ю часть текста. По определению вероятности эта величина равна вероятности появления символа в каждой позиции текста:
p=1/N.
Слайд 15
С позиции алфавитного подхода к измерению информации 1
бит – это информационный вес символа из двоичного алфавита.
Более крупной единицей измерения информации является байт.
1 байт – это информационный вес символа из алфавита мощностью 256. (1 байт = 8 бит)
Для представления текстов, хранимых и обрабатываемых в компьютере, чаще всего используется алфавит мощностью 256 символов. Следовательно, 1 символ такого текста «весит» 1 байт.
1 Кб (килобайт)=210 байт=1024 байта
1 Мб (мегабайт)=210 Кб=1024 Кб
1Гб (гигабайт)=210 Мб=1024 Мб
Слайд 16
Приближение разной вероятности символов в тексте
В этом приближении
учитывается, что в реальном тексте разные символы встречаются с
разной частотой. Отсюда следует, что вероятности появления разных символов в определенной позиции текста различны и, следовательно, различаются их информационные веса.
Статистический анализ русских текстов показывает, что частота появления буквы «о» составляет 0,09. Это значит, что на каждые 100 символов буква «о» в среднем встречается 9 раз. Это же число обозначает вероятность появления буквы «о» в определенной позиции текста: p0=0,09. Отсюда следует, что информационный вес буквы «о» в русском тексте равен 3,47393 бита.
Слайд 17
Измерение информации. Содержательный подход
С позиции содержательного подхода к
измерению информации решается вопрос о количестве информации в сообщении,
получаемом человеком. Рассматривается следующая ситуация:
человек получает сообщение о некотором событии; при этом заранее известна неопределенность знания человека об ожидаемом событии. Неопределенность знания может быть выражена либо числом возможных вариантов события, либо вероятностью ожидаемых вариантов события;
Слайд 18
2) в результате получения сообщения неопределенность знания снимается:
из некоторого возможного количества вариантов оказался выбранным один;
3) по
формуле вычисляется количество информации в полученном сообщении, выраженное в битах.
Формула, используемая для вычисления количества информации, зависит от ситуаций, которых может быть две:
Все возможные варианты события равновероятны. Их число конечно и равно N.
Вероятности (p) возможных вариантов события разные и они заранее известны:
{pi}, i=1..N. Здесь по-прежнему N – число возможных вариантов события.
Равновероятные события
Неравновероятные события
Слайд 19
Равновероятные события
Если обозначить буквой i количество информации
в сообщении о том, что произошло одно из N
равновероятных событий, то величины i и N связаны между собой формулой Хартли:
2i = N (1)
Величина I измеряется в битах. Отсюда следует вывод:
1 бит – это количество информации в сообщении об одном из двух равновероятных событий.
Формула Хартли – это показательное уравнение. Если i – неизвестная величина, то решением уравнения (1) будет:
(2)
Пример 1
Пример 2
Слайд 20
Пример 1
Задача.
Сколько информации содержит сообщение о
том, что из колоды карт достали даму пик?
Решение:
колода – 32 карты. В перемешанной колоде выпадение любой карты – равновероятное событие. Если i – количество информации в сообщении о том, что выпала конкретная карта (дама пик), то из уравнения Хартли:
2i = 32 = 25
Отсюда: I = 5 бит
Слайд 21
Пример 2
Задача.
Сколько информации содержит сообщение о
выпадении грани с числом 3 на шестигранном игральном кубике?
Решение:
Считая выпадение любой грани событием равновероятным, запишем формулу Хартли: 2i = 6. Отсюда:
бит
Слайд 22
Неравновероятные события
Если вероятность некоторого события равна p,
а i (бит) – это количество информации в сообщении
о том, что произошло это событие, то данные величины связаны между собой формулой:
2i = 1/p (*)
Решая показательное уравнение (*) относительно i, получаем:
Формула (**) была предложена К.Шенноном, поэтому ее называют формулой Шеннона
(**)
Слайд 23
Представление и кодирование информации
1. Язык как знаковая
система
2. Представление информации в живых организмах
3. Кодирование
информации
Слайд 24
Язык как знаковая система
Язык – это определенная
система символьного представления информации.
«Язык – это множество символов и
совокупность правил, определяющих способы составления из этих символов осмысленных сообщений» (словарь школьной информатики).
Т.к. осмысленное сообщение есть информация, то определения совпадают.
ЯЗЫК
естественные
формальные
Язык информатики
Слайд 25
Естественные языки
Исторически сложившиеся языки национальной речи.
Для большинства
современных языков характерно наличие устной и письменной форм речи.
Анализ естественных языков в большей степени является предметом филологических наук, в частности, лингвистики. В информатике анализом естественных языков занимаются специалисты в области искусственного интеллекта. Одна из целей разработки проекта ЭВМ пятого поколения – научить компьютер понимать естественные языки.
Слайд 26
Формальные языки
Искусственно созданные языки для профессионального применения.
Они, как
правило, носят международный характер и имеют письменную форму. Примерами
таких языков являются математика, язык химических формул, нотная грамота.
Для формальных языков характерна принадлежность к ограниченной предметной области. Назначение формального языка – адекватное описание системы понятий и отношений, свойственных для данной предметной области.
Слайд 27
С любым языком связаны следующие понятия:
алфавит –
это множество используемых символов;
синтаксис – правила записи языковых конструкций;
семантика
– смысловая сторона языковых конструкций;
прагматика – практические последствия применения текста на данном языке.
Естественные языки не ограничены в своем применении, в этом смысле их можно назвать универсальными. Однако не всегда бывает удобным использовать только естественный язык в узкопрофессиональных областях. В таких случаях люди прибегают к помощи формальных языков. Известны примеры языков, находящихся в промежуточном состоянии между естественными и формальными. Язык эсперанто был создан искусственно для общения людей разных национальностей. А латынь в наше время стала формальным языком медицины и фармакологии, утратив функцию разговорного языка.
Слайд 28
Представление информации в живых организмах
Человек воспринимает информацию об
окружающем мире с помощью органов чувств. Чувствительные нервные окончания
органов чувств воспринимают воздействие и передают его нейронам, цепи которых составляют нервную систему.
Нейрон может находиться в одном из двух состояний: невозбужденном и возбужденном. Возбужденный нейрон генерирует электрический импульс, который передается по нервной системе.
Состояние нейрона (нет импульса, есть импульс) можно рассматривать как знаки некоторого алфавита нервной системы, с помощью которого происходит передача информации.
Слайд 29
Генетическая информация во многом определяет строение и развитие
живых организмов и передается по наследству.
Хранится генетическая информация в
клетках организмов в структуре молекул ДНК (дезоксирибонуклеиновой кислоты). Молекула ДНК состоит из двух скрученных друг с другом в спираль цепей, построенных из четырех нуклеотидов: A, G, T, C, которые образуют генетический алфавит.
Молекула ДНК человека включает в себя около 3 миллиардов пар нуклеотидов и поэтому в ней закодирована вся информация об организме человека: его внешность, здоровье или предрасположенность к болезням, способности.
Слайд 30
Кодирование информации
Представление информации происходит в различных формах в
процессе восприятия окружающей среды живыми организмами и человеком, в
процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером и так далее.
Преобразование информации из одной формы представления в другую называется кодированием.
Все множество символов, используемых для кодирования, называется алфавитом кодирования. Например, в памяти компьютера любая информация кодируется с помощью двоичного алфавита, содержащего всего два символа: 0 и 1.
Слайд 31
В процессе обмена информацией часто приходится производить операции
кодирования и декодирования информации. При вводе знака алфавита в
компьютер путем нажатия соответствующей клавиши на клавиатуре происходит кодирование знака, то есть преобразование его в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс – декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение.
Слайд 32
Представление числовой информации с помощью систем счисления
Система счисления
Десятичная
система счисления
Двоичная система счисления
Позиционные системы счисления с произвольным основанием
Слайд 33
Система счисления
Для записи информации о количестве объектов
используются числа. Числа записываются с использованием особых знаковых систем,
которые называются системами счисления.
Система счисления – это способ изображения чисел и соответствующие ему правила действия над числами.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные.
Знаки, используемые при записи чисел, называются цифрами.
Слайд 34
Непозиционные системы счисления
В непозиционных системах счисления значение цифры
не зависит от положения в числе.
Примером непозиционной системы
счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
I V X L C D M
1 5 10 50 100 500 1000
Пример Пример 1 ПримерПример 1 Пример 2 Пример 3
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же записана меньшая цифра, а справа – большая, то их значения вычитаются.
Слайд 35
Пример 1
Число CCXXXII складывается из
двух сотен, трех десятков и двух единиц и равно
двумстам тридцати двум.
Слайд 36
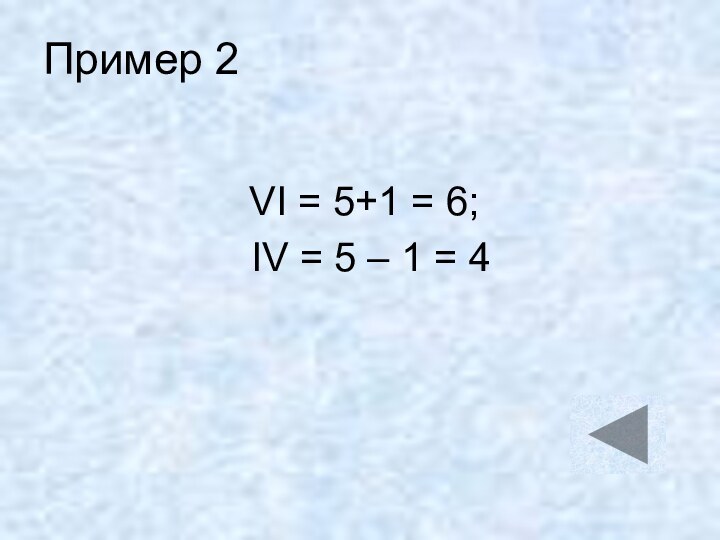
Пример 2
VI = 5+1 = 6;
IV
= 5 – 1 = 4
Слайд 37
Пример 3
MCMXCVIII = 1000 + (-
100 + 1000) + + (-
10 + 100) + 5 + 1 + 1 + 1 = 1998
Слайд 38
Позиционные системы счисления
Первая позиционная система счисления была придумана
еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной,
то есть в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60.
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину: в сутках две дюжины часов, круг содержит тринадцать дюжин градусов и так далее
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.
Слайд 39
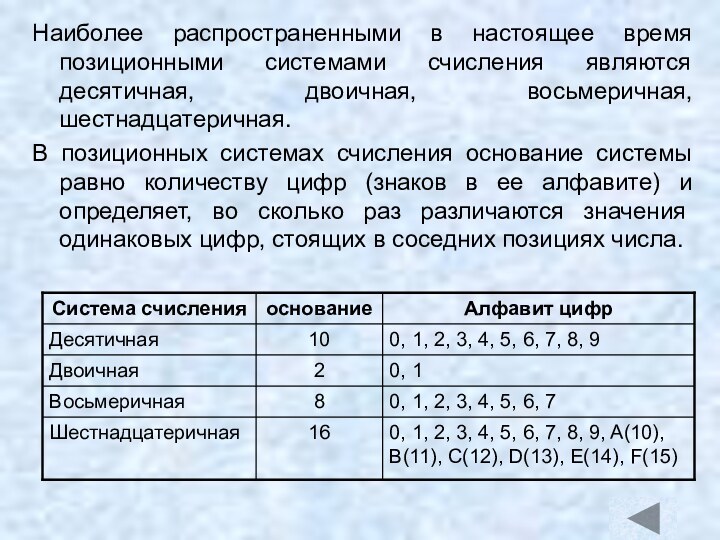
Наиболее распространенными в настоящее время позиционными системами счисления
являются десятичная, двоичная, восьмеричная, шестнадцатеричная.
В позиционных системах счисления основание
системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.
Слайд 40
Десятичная система счисления
Рассмотрим в качестве примера десятичное число
555.
Цифра 5 встречается трижды, причем самая правая цифра 5
обозначает 5 единиц, вторая справа – пять десятков и, наконец, третья справа – пять сотен.
Позиция цифры в числе называется ….
Разряд числа возрастает справа налево, от младших разрядов к старшим.
Число 555 – свернутая форма записи числа.
В развернутой форме записи числа умножение цифры числа на различные степени числа 10 записывается в явной форме. Т.о.
разрядом
Слайд 41
В общем случае в десятичной системе счисления запись
числа А10, которое содержит n целых разрядов числа и
m дробных разрядов числа, выглядит так:
Коэффициенты ai в этой записи являются цифрами десятичного числа, которое в свернутой форме записывается так:
Из вышеприведенных формул видно, что умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево.
Слайд 42
Двоичная система счисления
В двоичной системе счисления основание равно
2, а алфавит состоит из двух цифр (0 и
1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа может выглядеть так,
Слайд 43
В общем случае в двоичной системе запись числа
А2, которое содержит n целых разрядов числа и m
дробных разрядов числа, выглядит так:
Свернутая запись двоичного числа:
Из вышеприведенных формул видно, что умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево.
Слайд 44
Позиционные системы счисления с произвольным основанием
Возможно использование множества
позиционных систем счисления, основание которых равно или больше 2.
В системах счисления с основанием q (q-ичная система счисления) числа в развернутой форме записываются в виде суммы степеней основания q с коэффициентами, в качестве которых выступают цифры 0, 1, q-1:
Коэффициенты ai в этой записи являются цифрами числа, записанного в q- ичной системе счисления.
Слайд 45
Так, в восьмеричной системе основание равно восьми (q=8).
Тогда записанное в свернутой форме восьмеричное число A8=673,28 в
развернутой форме будет иметь вид:
В шестнадцатеричной системе основание равно шестнадцати (q=16), тогда записанное в свернутой форме шестнадцатеричное число A16=8A,F16 в развернутой форме будет иметь вид:
Если выразить шестнадцатеричные цифры через их десятичные значения, то запись числа примет вид:
Слайд 46
Перевод чисел в позиционных системах счисления
Перевод чисел в
десятичную систему счисления
Перевод чисел из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Слайд 47
Перевод чисел в десятичную систему счисления
Преобразование чисел,
представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в
десятичную выполнить довольно легко. Для этого необходимо записать число в развернутой форме и вычислить его значение
Перевод числа из двоичной системы в десятичную
Перевод чисел из восьмеричной системы в десятичную
Перевод чисел из шестнадцатеричной системы в десятичную
Слайд 48
Перевод числа из двоичной системы в десятичную
10,112
Перевести
в десятичную систему следующие числа:
1012, 1102, 101,012
Слайд 49
Перевод чисел из восьмеричной системы в десятичную
67,58
Перевести в
десятичную систему следующие числа: 78,118, 228, 34,128
Слайд 50
Перевод чисел из шестнадцатеричной системы в десятичную
19F16
(F=15)
Перевести в десятичную систему счисления следующие числа: 1A16, BF16,
9C,1516
Слайд 51
Перевод чисел из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную
Перевод чисел из десятичной системы в
двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере перевода чисел из десятичной системы в двоичную. При этом необходимо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут различаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
Алгоритм перевода правильных десятичных дробей в двоичную систему счисления.
Перевод чисел из системы с основанием p в систему с основанием q
Слайд 52
Алгоритм перевода целых десятичных чисел в двоичную систему
счисления
Последовательно выполнять деление исходного целого десятичного числа и получаемых
целых частных на основание системы до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.
Записать полученные остатки в обратной последовательности.
ПРИМЕР
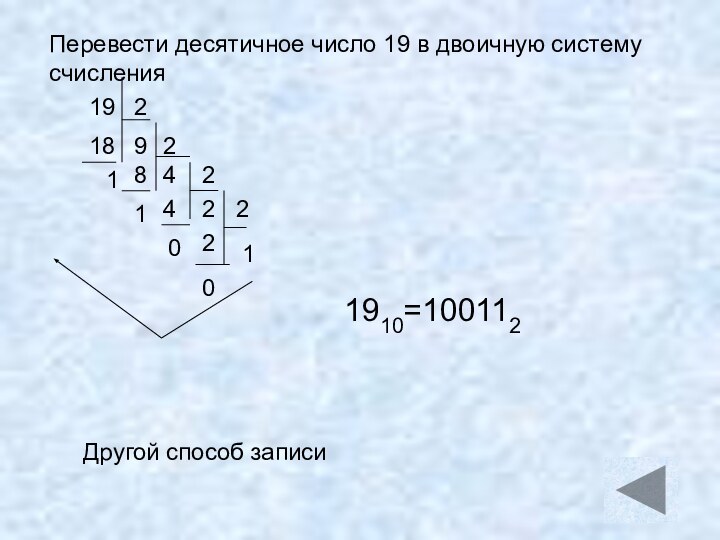
Слайд 53
19
2
9
18
1
2
4
8
1
2
2
4
0
2
1
2
0
1910=100112
Перевести десятичное число 19 в двоичную систему счисления
Другой
способ записи
Слайд 54
Алгоритм перевода правильных десятичных дробей в двоичную систему
счисления.
Последовательно выполнять умножение исходной десятичной дроби и получаемых дробных
частей произведений на основание системы (на 2) до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычислений.
Записать полученные целые части произведения в прямой последовательности.
ПРИМЕР
Слайд 55
Перевести 0,7510 в двоичную систему счисления
А2=0,а-1а-2=0,112
Слайд 56
Перевод чисел из системы с основанием p в
систему с основанием q
Перевод чисел из позиционной системы с
произвольным основанием p в систему с основанием q производится по алгоритмам, аналогичным рассмотренным выше.
Рассмотрим алгоритм перевода целых чисел на примере перевода целого десятичного числа 42410 в шестнадцатеричную систему, то есть из системы счисления с основанием p=10 в систему счисления с основанием q=16.
В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае в десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае шестнадцатеричной).
Слайд 57
Рассмотрим теперь алгоритм перевода дробных чисел на примере
перевода десятичной дроби А10=0,625 в восьмеричную систему, то есть
из системы счисления с основанием p=10 в систему счисления с основанием q=8.
Перевод чисел, содержащих и целую и дробную части, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно – дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.
Слайд 58
Перевод чисел из двоичной системы счисления в восьмеричную
и шестнадцатеричную и обратно
Перевод чисел между системами
счисления, основания которых являются степенями числа 2 (q=2n), может производиться по более простым алгоритмам. Такие алгоритмы могут применяться для перевода чисел между двоичной (q=21), восьмеричной (q=23) и шестнадцатеричной (q=24) системами счисления.
Перевод чисел из двоичной системы счисления в восьмеричную.
Перевод чисел из двоичной системы счисления в шестнадцатеричную.
Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную.
Слайд 59
Перевод чисел из двоичной системы счисления в восьмеричную.
Для
записи двоичных чисел используются две цифры, то есть в
каждом разряде числа возможны 2 варианта записи. Решаем показательное уравнение:
2=2I. Так как 2=21, то I= 1 бит.
Каждый разряд двоичного числа содержит 1 бит информации.
Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение:
8=2I. Так как 8=23, то I= 3 бита.
Каждый разряд восьмеричного числа содержит 3 бита информации.
Слайд 60
Таким образом, для перевода целого двоичного числа в
восьмеричное его нужно разбить на группы по три цифры,
справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012
Для упрощения перевода можно использовать таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры.
Слайд 61
Для перевода дробного двоичного числа (правильной дроби) в
восьмеричное необходимо разбить его на триады слева направо(не учитывая
нуль до запятой) и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями. Далее необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число A2=0,1101012 в восьмеричную систему счисления:
110 101 0,658
Слайд 62
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Для
записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в
каждом разряде числа возможны 16 вариантов записи. Решаем показательное уравнение:
16=2I. Так как 16=24, то I= 4 бита.
Каждый разряд восьмеричного числа содержит 4 бита информации.
Слайд 63
Таким образом, для перевода целого двоичного числа в
шестнадцатеричное его нужно разбить на группы по четыре цифры
(тетрады), справа налево, и если в последней, левой, группе окажется меньше четырех цифр, то необходимо ее дополнить слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо(не учитывая нуль до запятой) и, если в последней, правой, группе окажется меньше четырех цифр, дополнить ее справа нулями. Далее необходимо тетрады заменить на шестнадцатеричные числа.
Таблица преобразования тетрад в шестнадцатеричные числа
Слайд 64
Перевод чисел из восьмеричной и шестнадцатеричной систем счисления
в двоичную
Для перевода чисел из восьмеричной и шестнадцатеричной систем
счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа – в группу из четырех цифр (тетраду).
Слайд 65
Арифметические операции в позиционных системах счисления
Арифметические операции во
всех позиционных системах счисления выполняются по одним и тем
же хорошо известным вам правилам.
Сложение
Вычитание
Умножение
Деление
Слайд 66
Сложение
Рассмотрим сложение чисел в двоичной системе счисления.
В его основе лежит таблица сложения одноразрядных двоичных чисел:
0+0=0
0+1=1
1+0=1
1+1=10
Слайд 67
Вычитание
Рассмотрим вычитание двоичных чисел. В его
основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании
из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:
Слайд 68
Умножение
В основе умножения лежит таблица умножения одноразрядных
двоичных чисел:
Слайд 69
Деление
Операция деления выполняется по алгоритму, подобному алгоритму
выполнения операции деления в десятичной системе счисления.
Слайд 70
Представление чисел в компьютере
Представление чисел в формате
с фиксированной запятой
2. Представление чисел в формате с плавающей
запятой
Слайд 71
Представление чисел в формате с фиксированной запятой
Целые числа
в компьютере хранятся в памяти в формате с фиксированной
запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «запятая» «находится» справа после младшего разряда, то есть вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2=111100002 будет храниться в ячейке памяти следующим образом:
Слайд 72
Максимальное значение целого неотрицательного числа достигается в случае,
когда во всех ячейках хранятся единицы. Для n-разрядного представления
оно будет равно
2n – 1.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно
Диапазон изменения целых неотрицательных чисел: от 0 до 255
Слайд 73
Для хранения целых чисел со знаком отводится две
ячейки памяти (16 битов), причем старший (левый) разряд отводится
под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное - 1).
Представление в компьютере положительных чисел с использованием формата «знак - величина» называется прямым кодом числа. Например, число 200210=111110100102 будет представлено в 16-разрядном представлении следующим образом:
Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:
A = 2n-1 - 1
Слайд 74
Для представления отрицательных чисел используется дополнительный код. Дополнительный
код позволяет заменить арифметическую операцию вычитания операцией сложения, что
существенно упрощает работу процессора и увеличивает его быстродействие.
Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2n - |A|.
Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:
1. Модуль числа записать в прямом коде в n двоичных разрядах.
2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).
3. К полученному обратному коду прибавить единицу.
ПРИМЕР
Слайд 75
Достоинствами представления чисел в формате с фиксированной запятой
являются простота и наглядность представления чисел, а также простота
алгоритмов реализации арифметических операций.
Недостатком представления чисел в формате с фиксированной запятой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.
Слайд 76
Записать дополнительный код отрицательного числа -2002 для 16-разрядного
компьютерного представления
Слайд 77
Представление чисел в формате с плавающей запятой
Вещественные числа
хранятся и обрабатываются в компьютере в формате с плавающей
запятой. В этом случае положение запятой в записи числа может изменяться.
Формат числа с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде:
где m – мантисса числа; q – основание системы счисления; n – порядок числа.
Слайд 78
Это означает, что мантисса должна быть правильной дробью
и иметь после запятой цифру, отличную от нуля.
Преобразуем десятичное
число 555,55, записанное в естественной форме, в экспоненциальную форму с нормализованной мантиссой:
Здесь нормализованная мантисса: m=0,55555, порядок: n=3.
Слайд 79
Двоичное кодирование информации
Двоичное кодирование текстовой информации
Двоичное кодирование графической
информации
Двоичное кодирование звуковой информации
Слайд 80
Двоичное
кодирование
текстовой
информации
Сообщение учащегося
Слайд 81
Двоичное
кодирование
графической
информации
Сообщение учащегося
Слайд 82
Двоичное
кодирование
звуковой
информации
Сообщение учащегося