- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Криптография. Симметричные алгоритмы шифрования
Содержание
- 2. Криптография. Симметричные алгоритмы шифрования.Введение.Терминология.Симметричные криптосистемы.Алгоритм Цезаря.Алгоритм замены полиалфавитный.Алгоритм замены с большим ключом.Перестановки.Гаммирование.
- 3. ВведениеПроблема защиты информации путем ее преобразования, исключающего
- 4. ВведениеПервоначально письменность сама по себе была криптографической
- 5. ВведениеС широким распространением письменности криптография стала формироваться
- 6. ВведениеБурное развитие криптографические системы получили в годы
- 7. Актуальность использования криптографических методов в информационных системахРасширилось
- 8. Актуальность использования криптографических методов в информационных системах2.
- 9. КРИПТОЛОГИЯ- занимается проблемой защиты информации путем ее преобразования (kryptos - тайный, logos - наука).
- 10. Направления криптологииКриптография.Криптоанализ.
- 11. ЦЕЛЬ КРИПТОГРАФИИКриптография занимается поиском и исследованием математических
- 12. ЦЕЛЬ КРИПТОАНАЛИЗА- исследование возможности расшифровывания информации без знания ключей.
- 13. РАЗДЕЛЫ КРИПТОГРАФИИ1. Симметричные криптосистемы.2. Криптосистемы с открытым ключом.3. Системы электронной подписи.4. Управление ключами.
- 14. Основные направления использования криптографических методовПередача конфиденциальной информации
- 15. Алфавиты, используемые в современных ИСАлфавит Z33 –
- 16. ШИФРОВАНИЕ- преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом.
- 17. ДЕШИФРОВАНИЕ- обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный.
- 18. КЛЮЧ- информация, необходимая для шифрования и дешифрования
- 19. Виды криптосистемСимметричные.Асимметричные (другие названия: несимметричные или системы с открытым ключом).
- 20. СИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ- для шифрования, и для дешифрования используется один и тот же ключ.
- 21. СИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ- используются два ключа
- 22. ПОТОКОВЫЕ АЛГОРИТМЫВ потоковых алгоритмах способ шифрования отдельного символа не зависит от соседних символов.
- 23. БЛОКОВЫЕ АЛГОРИТМЫВ блоковых алгоритмах сообщение разбивается на
- 24. ЭЛЕКТРОННАЯ (ЦИФРОВАЯ) ПОДПИСЬ- присоединяемое к тексту его
- 25. КРИПТОСТОЙКОСТЬ- характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. криптоанализу).
- 26. Показатели криптостойкостиКоличество всех возможных ключей.Среднее время, необходимое для криптоанализа.
- 27. Слабые ключиключи, которые предсказуемо преобразуют некоторый текст
- 28. ШифрШифром называют пару: алгоритм и ключ.Эффективность шифрования зависит от сохранения тайны ключа и криптостойкости шифра.
- 29. Метод грубой силыМетод «грубой силы» предполагает перебор всех возможных ключей.
- 30. Криптостойкий алгоритмАлгоритм называют криптостойким, если не существует
- 31. Симметричные криптосистемыПрежде, чем начать использовать систему, необходимо
- 32. Базовые классы симметричных криптосистемАлгоритмы подстановки или замены.Алгоритмы перестановки. Алгоритмы гаммирования.
- 33. Моноалфавитные подстановки- это наиболее простой вид преобразований,
- 34. Алгоритм ЦезаряСамый древний алгоритм, предложенный Юлием Цезарем.
- 35. Алгоритм ЦезаряИдея состоит в следующем: задан алфавит
- 36. Алгоритм замены полиалфавитныйУсложнить шифр можно, используя не
- 37. Алгоритм замены полиалфавитныйОчевидно, что во всех алфавитах
- 38. Пример алгоритма замены полиалфавитногоПусть дан первый алфавит
- 39. Пример алгоритма замены полиалфавитногоПусть дан первый алфавит
- 40. Алгоритм замены с большим ключомДля обеспечения высокой
- 41. Алгоритм замены с большим ключомМожно говорить здесь
- 42. Проблемы использования алгоритма с большим ключомЭтот способ
- 43. Проблемы использования алгоритма с большим ключомЧем больше
- 44. Алгоритм замены с большим ключомТак, например, криптокарта
- 45. Схема с одноразовым блокнотом- применяет алгоритм Диффи-Хэлмана для генерации очередного секретного ключа.
- 46. Пример алгоритма заменыПример 1. Пусть дан алфавит
- 47. Пример алгоритма заменыПример 1. Пусть дан алфавит
- 48. Пример алгоритма заменыПример 2. Пусть дан алфавит
- 49. Пример алгоритма заменыКоды «з» - 231, «а»
- 50. Пример алгоритма заменыКоды «з» - 231, «а»
- 51. Пример алгоритма заменыПосле «з» вторая буква «к».Код
- 52. Пример алгоритма заменыТ.к. здесь результат шифрования зависим
- 53. Перестановки- несложный метод криптографического преобразования, заключающийся в перестановке местами символов исходного текста по некоторому правилу.
- 54. ПерестановкиБлоки информации (байты, биты, более крупные единицы)
- 55. Ключ алгоритма перестановки- множество пар переставляемых символом. Часто его задают в виде таблицы перемешивания.
- 56. Пример алгоритма перестановкиПравило перестановок зададим следующее: первый
- 57. Пример алгоритма перестановкиПокажем результат шифрования по шагам:
- 58. Гаммирование- представляет собой преобразование исходного текста, при
- 59. ГаммированиеВ случае если последовательность является истинно случайной
- 60. ГаммированиеГаммирование является также широко применяемым криптографическим преобразованием.
- 61. Принцип шифрования гаммированием- заключается в генерации гаммы
- 62. Принцип дешифрования при гаммировании- сводится к повторной
- 63. Гамма шифраПолученный зашифрованный текст является достаточно трудным
- 64. Гамма шифраФактически же, если период гаммы превышает
- 65. Недостатки метода гаммирования1. Метод гаммирования становится бессильным,
- 66. Недостатки метода гаммирования2. Если гамма получена в
- 67. Недостатки метода гаммированияЗлоумышленник может сделать предположение о
- 68. Виды гаммированиябитовое гаммирование;гаммирование в общем виде.
- 69. Битовое гаммирование- исходный текст складывается с гаммой при помощи операции XOR (сложение по модулю)
- 70. Гаммирование в общем виде- сложение идет по модулю числа, равного длине алфавита.
- 71. Пример модульного сложения букв
- 72. Пример модульного вычитания букв
- 73. Пример гаммирования в общем видеПусть дан алфавит
- 74. Пример гаммирования в общем видеПусть дан алфавит
- 75. Скачать презентацию
- 76. Похожие презентации
Криптография. Симметричные алгоритмы шифрования.Введение.Терминология.Симметричные криптосистемы.Алгоритм Цезаря.Алгоритм замены полиалфавитный.Алгоритм замены с большим ключом.Перестановки.Гаммирование.









































































Слайд 2
Криптография. Симметричные алгоритмы шифрования.
Введение.
Терминология.
Симметричные криптосистемы.
Алгоритм Цезаря.
Алгоритм замены полиалфавитный.
Алгоритм
замены с большим ключом.
Слайд 3
Введение
Проблема защиты информации путем ее преобразования, исключающего ее
прочтение посторонним лицом, волновала человеческий ум с давних времен.
История криптографии - ровесница истории человеческого языка.
Слайд 4
Введение
Первоначально письменность сама по себе была криптографической системой,
так как в древних обществах ею владели только избранные.
Священные книги Древнего Египта, Древней Индии тому примеры.
Слайд 5
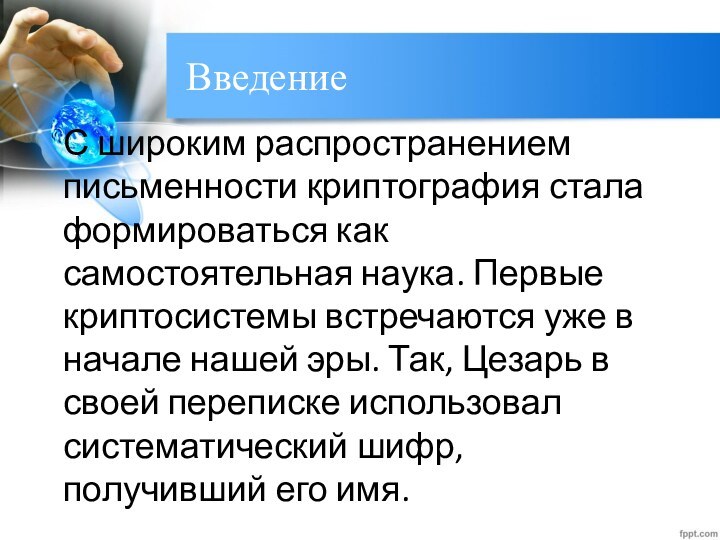
Введение
С широким распространением письменности криптография стала формироваться как
самостоятельная наука. Первые криптосистемы встречаются уже в начале нашей
эры. Так, Цезарь в своей переписке использовал систематический шифр, получивший его имя.
Слайд 6
Введение
Бурное развитие криптографические системы получили в годы первой
и второй мировых войн. Начиная с послевоенного времени, и
по нынешний день появление вычислительных средств ускорило разработку и совершенствование криптографических методов.
Слайд 7
Актуальность использования криптографических методов в информационных системах
Расширилось использование
компьютерных сетей, в частности глобальной сети Интернет, по которым
передаются большие объемы информации государственного, военного, коммерческого и частного характера, не допускающего возможность доступа к ней посторонних лиц;
Слайд 8
Актуальность использования криптографических методов в информационных системах
2. появление
новых мощных компьютеров, технологий сетевых и нейронных вычислений дискредитировало
множество криптографических систем еще недавно считавшихся практически не раскрываемыми.
Слайд 9
КРИПТОЛОГИЯ
- занимается проблемой защиты информации путем ее преобразования
(kryptos - тайный, logos - наука).
Слайд 11
ЦЕЛЬ КРИПТОГРАФИИ
Криптография занимается поиском и исследованием математических методов
преобразования информации с целью ее защиты от несанкционированного доступа.
Слайд 13
РАЗДЕЛЫ КРИПТОГРАФИИ
1. Симметричные криптосистемы.
2. Криптосистемы с открытым ключом.
3.
Системы электронной подписи.
4. Управление ключами.
Слайд 14
Основные направления использования криптографических методов
Передача конфиденциальной информации по
каналам связи (например, электронная почта).
Установление подлинности передаваемых сообщений.
Хранение
информации (документов, баз данных) на носителях в зашифрованном виде.
Слайд 15
Алфавиты, используемые в современных ИС
Алфавит Z33 – 33
буквы русского алфавита и пробел.
Алфавит Z256 – символы, входящие
в стандартные коды ASCII и КОИ-8.Алфавит Z2 – {0,1}.
Восьмеричный алфавит.
Шестнадцатеричный алфавит.
Слайд 16
ШИФРОВАНИЕ
- преобразовательный процесс: исходный текст, который носит также
название открытого текста, заменяется шифрованным текстом.
Слайд 17
ДЕШИФРОВАНИЕ
- обратный шифрованию процесс. На основе ключа шифрованный
текст преобразуется в исходный.
Слайд 18
КЛЮЧ
- информация, необходимая для шифрования и дешифрования текстов.
Обычно ключ представляет собой последовательный ряд букв алфавита.
Слайд 19
Виды криптосистем
Симметричные.
Асимметричные (другие названия: несимметричные или системы с
открытым ключом).
Слайд 20
СИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ
- для шифрования, и для дешифрования используется
один и тот же ключ.
Слайд 21
СИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ
- используются два ключа -
открытый и закрытый (секретный), которые математически связаны друг с
другом. Информация шифруется с помощью открытого ключа и расшифровывается с помощью закрытого. Либо наоборот, шифруется с помощью закрытого ключа и расшифровывается с помощью открытого.
Слайд 22
ПОТОКОВЫЕ АЛГОРИТМЫ
В потоковых алгоритмах способ шифрования отдельного символа
не зависит от соседних символов.
Слайд 23
БЛОКОВЫЕ АЛГОРИТМЫ
В блоковых алгоритмах сообщение разбивается на блоки,
в которых способ шифрования символов зависит от их положения
и окружения.
Слайд 24
ЭЛЕКТРОННАЯ (ЦИФРОВАЯ) ПОДПИСЬ
- присоединяемое к тексту его криптографическое
преобразование, которое позволяет при получении текста другим пользователем проверить
авторство и подлинность сообщения.
Слайд 25
КРИПТОСТОЙКОСТЬ
- характеристика шифра, определяющая его стойкость к дешифрованию
без знания ключа (т.е. криптоанализу).
Слайд 26
Показатели криптостойкости
Количество всех возможных ключей.
Среднее время, необходимое для
криптоанализа.
Слайд 27
Слабые ключи
ключи, которые предсказуемо преобразуют некоторый текст (или
множество текстов).
Примеры слабых ключей: шаг, равный 0 в
алгоритме Цезаря; гамма, состоящая из одних нулей в гаммировании.
Слайд 28
Шифр
Шифром называют пару: алгоритм и ключ.
Эффективность шифрования зависит
от сохранения тайны ключа и криптостойкости шифра.
Слайд 30
Криптостойкий алгоритм
Алгоритм называют криптостойким, если не существует способов
вскрытия зашифрованного текста без знания ключа, дающих результат быстрее,
чем метод грубой силы.
Слайд 31
Симметричные криптосистемы
Прежде, чем начать использовать систему, необходимо получить
общий секретный ключ так, чтобы исключить к нему доступ
потенциального злоумышленника.
Слайд 32
Базовые классы симметричных криптосистем
Алгоритмы подстановки или замены.
Алгоритмы перестановки.
Алгоритмы гаммирования.
Слайд 33
Моноалфавитные подстановки
- это наиболее простой вид преобразований, заключающийся
в замене символов исходного текста на другие (того же
алфавита) по более или менее сложному правилу. В случае моноалфавитных подстановок каждый символ исходного текста преобразуется в символ шифрованного текста по одному и тому же закону.
Слайд 34
Алгоритм Цезаря
Самый древний алгоритм, предложенный Юлием Цезарем.
В
настоящее время не может использоваться, так как его криптостойкость
чрезвычайно мала.
Слайд 35
Алгоритм Цезаря
Идея состоит в следующем: задан алфавит и
задан шаг (целое число). Шифрование заключается в замене символа
исходного текста на символ, отстоящий в алфавите на шаг вправо. Важно, что алфавит рассматривается как «склеенная в кольцо» последовательность символов, то есть вслед за последним символом алфавита идет снова первый.
Слайд 36
Алгоритм замены полиалфавитный
Усложнить шифр можно, используя не один,
а несколько алфавитов. Алфавиты могут различаться количеством и порядком
символов.
Слайд 37
Алгоритм замены полиалфавитный
Очевидно, что во всех алфавитах должны
быть все символы исходного текста и, возможно, еще какие-то.
Алфавиты перебираются по некоторому закону, который определен ключом или задан в алгоритме. Одному символу исходного текста соответствует один или несколько символов результирующего.
Слайд 38
Пример алгоритма замены полиалфавитного
Пусть дан первый алфавит «аяздкв
бмл», второй «яозеадивлкн» и
третий «аколд кмзв».
Пусть алфавиты
используются по очереди. Шаг равен 5. Исходный текст «задавака».
Тогда результат шифрования:
Слайд 39
Пример алгоритма замены полиалфавитного
Пусть дан первый алфавит «аяздкв
бмл», второй «яозеадивлкн» и
третий «аколд кмзв».
Пусть алфавиты
используются по очереди. Шаг равен 5. Исходный текст «задавака».
Тогда результат шифрования: «бквво лк».
Слайд 40
Алгоритм замены с большим ключом
Для обеспечения высокой криптостойкости
требуется использование больших ключей. Большой ключ приводит к тому,
что одна и та же буква исходного текста будет преобразовываться в зашифрованную с разными ключами.
Слайд 41
Алгоритм замены с большим ключом
Можно говорить здесь о
криптосистеме с одноразовым ключом, то есть ключ настолько большой,
что каждый следующий текст шифруется уже с другой его частью. Такой шифр обладает абсолютной теоретической стойкостью, так как взлом одного сообщения не дает никакой информации для взлома другого.
Слайд 42
Проблемы использования алгоритма с большим ключом
Этот способ неудобен
для практического применения. Основная его проблема состоит в том,
что для расшифрования требуется заранее некоторым секретным способом передать ключ.
Слайд 43
Проблемы использования алгоритма с большим ключом
Чем больше ключ,
тем проблематичнее передача. Можно, конечно, передать не сам ключ,
а алгоритм его формирования. Но тогда этот алгоритм должен быть секретным.
Слайд 44
Алгоритм замены с большим ключом
Так, например, криптокарта Forteza,
используемая агентами национальной безопасности США, базируется на том, что
и отправитель и получатель одновременно генерируют одинаковый ключ, пользуясь неким аппаратным средством.
Слайд 45
Схема с одноразовым блокнотом
- применяет алгоритм Диффи-Хэлмана для
генерации очередного секретного ключа.
Слайд 46
Пример алгоритма замены
Пример 1. Пусть дан алфавит
«аяздкв
бмл».
Ключ, то есть множество шагов: 1, 5, 3,
7, 2, 6, 4, 1, 7, 3, 3. Исходный текст «задавака».
Тогда результат шифрования:
Слайд 47
Пример алгоритма замены
Пример 1. Пусть дан алфавит
«аяздкв
бмл».
Ключ, то есть множество шагов: 1, 5, 3,
7, 2, 6, 4, 1, 7, 3, 3. Исходный текст «задавака».
Тогда результат шифрования: «дв бб мя».
Слайд 48
Пример алгоритма замены
Пример 2. Пусть дан алфавит «аяздкв
бмл». Задан ключ, то есть алгоритм его вычисления: для
шифрования первого символа берется шаг, равный 2, а для каждого последующего – шаг, равный остатку от деления на 10 кода предыдущего исходного символа (номера в таблице ASCII). Исходный текст «задавака».
Слайд 49
Пример алгоритма замены
Коды «з» - 231, «а» -
224, «д» - 228, «в» - 226, «к» -
234.Тогда результат шифрования:
Слайд 50
Пример алгоритма замены
Коды «з» - 231, «а» -
224, «д» - 228, «в» - 226, «к» -
234.Тогда результат шифрования: «ккякякмк».
Слайд 51
Пример алгоритма замены
После «з» вторая буква «к».
Код буквы
«а» 224.
224 mod 10 =
4.четвертая буква после «а» - «к».
3. Код буквы «д» 228.
228 mod 10 = 8.
восьмая буква после «д» - «я».
4. ……..
Слайд 52
Пример алгоритма замены
Т.к. здесь результат шифрования зависим от
исходного текста, то такой алгоритм можно отнести к блоковым.
Слайд 53
Перестановки
- несложный метод криптографического преобразования, заключающийся в перестановке
местами символов исходного текста по некоторому правилу.
Слайд 54
Перестановки
Блоки информации (байты, биты, более крупные единицы) не
изменяются сами по себе, но изменяется их порядок следования,
что делает информацию нечитаемой для стороннего наблюдателя. Шифры перестановок в настоящее время не используются в чистом виде, так как их криптостойкость недостаточна.
Слайд 55
Ключ алгоритма перестановки
- множество пар переставляемых символом. Часто
его задают в виде таблицы перемешивания.
Слайд 56
Пример алгоритма перестановки
Правило перестановок зададим следующее: первый символ
исходного текста меняется местами с символом, номер которого задан
в таблице первым. Второй символ уже не совсем исходного текста – с символом, номер которого задан в таблице вторым и т.д. Пусть задана таблица: 4, 3, 2. Если таблица заканчивается, начинается отсчет символов в шифруемом тексте с 1. Исходный текст «задавака».
Слайд 57
Пример алгоритма перестановки
Покажем результат шифрования по шагам: 1
буква меняется местами с 4 «аадзвака», 2 с 3
«адазвака», 3 со 2 «аадзвака», 4 с 4 «аадзвака», 5 с 3 «аавздака», 6 со 2 «аавздака», 7 с 4 «аавкдаза», 8 с 3 «ааакдазв». Расшифрование проводится в обратном порядке.
Слайд 58
Гаммирование
- представляет собой преобразование исходного текста, при котором
символы исходного текста складываются (по модулю, равному мощности алфавита)
с символами некоторой заданной или генерируемой псевдослучайной последовательности, вырабатываемой по некоторому правилу.
Слайд 59
Гаммирование
В случае если последовательность является истинно случайной (например,
снятой с физического датчика) и каждый ее фрагмент используется
только один раз, мы получаем криптосистему с одноразовым ключом. Системы с одноразовым ключом (как особо надежные) применяются в правительственной связи.
Слайд 60
Гаммирование
Гаммирование является также широко применяемым криптографическим преобразованием. На
самом деле граница между гаммированием и использованием бесконечных ключей
(и шифров Вижинера) весьма условная.
Слайд 61
Принцип шифрования гаммированием
- заключается в генерации гаммы шифра
и наложении полученной гаммы на открытые данные обратимым образом
(например, используя сложение по модулю 2).
Слайд 62
Принцип дешифрования при гаммировании
- сводится к повторной генерации
гаммы шифра при известном ключе (он нужен для того
чтобы сгенерировать ту же самую гамму) и наложении такой гаммы на зашифрованные данные.
Слайд 63
Гамма шифра
Полученный зашифрованный текст является достаточно трудным для
раскрытия в том случае, если гамма шифра не содержит
повторяющихся битовых последовательностей. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого слова.
Слайд 64
Гамма шифра
Фактически же, если период гаммы превышает длину
всего зашифрованного текста и неизвестна никакая часть исходного текста,
то шифр можно раскрыть только прямым перебором (методом «грубой силы»). Криптостойкость в этом случае определяется размером ключа.
Слайд 65
Недостатки метода гаммирования
1. Метод гаммирования становится бессильным, если
злоумышленнику становится известен фрагмент исходного текста и соответствующая ему
шифрограмма. Простым вычитанием по модулю получается отрезок гаммы.
Слайд 66
Недостатки метода гаммирования
2. Если гамма получена в результате
работы генератора псевдослучайных чисел (то есть программно), то знание
фрагмента псевдослучайной последовательности может оказаться (почти всегда!) достаточным для восстановления всей последовательности. Фрагмент текста не обязательно должен быть украден.
Слайд 67
Недостатки метода гаммирования
Злоумышленник может сделать предположение о содержании
исходного текста. Так, если большинство посылаемых сообщений начинается со
слов “СОВ. СЕКРЕТНО”, то криптоанализ всего текста значительно облегчается, т.к. 13 символов гаммы можно определить. Это следует учитывать при создании реальных систем информационной безопасности.
Слайд 69
Битовое гаммирование
- исходный текст складывается с гаммой
при помощи операции XOR (сложение по модулю)
Слайд 73
Пример гаммирования в общем виде
Пусть дан алфавит «абюя
123». В этом алфавите символы пронумерованы от 0 до
7. Длина алфавита равна 8. Пусть у нас есть сообщение «а13» и гамма «ю2». Зашифруем:а13
ю2ю
Слайд 74
Пример гаммирования в общем виде
Пусть дан алфавит «абюя
123». В этом алфавите символы пронумерованы от 0 до
7. Длина алфавита равна 8. Пусть у нас есть сообщение «а13» и гамма «ю2». Зашифруем:а13 -> юяб
ю2ю