Презентация на тему Квантовые игры и теоретико-игровые основания прагматики

|2 + | β |2 = 1
 

кубит
n-кубитный регистр
 
 
NOT
 
Переключатель знака

состояния

 

регистры Паули

 

 

Преобразование Адамара

)

Примени последовательность унитарных преобразований

Проделай измерение для считывания состояния

игроков
S = S1 × S2 × … × Sn

, где Si, i = 1,…,n – пространства стратегий
u = u1 × … × un, где ui(s1,…,sn), i = 1,…,n – функции выигрыша,
sn∈ Si

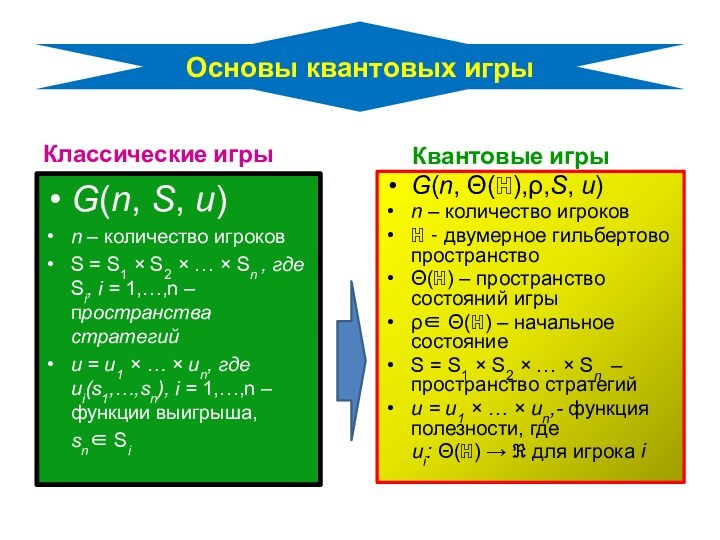
Квантовые игры

G(n, Θ(ℍ),ρ,S, u)
n – количество игроков
ℍ - двумерное гильбертово пространство
Θ(ℍ) – пространство состояний игры
ρ∈ Θ(ℍ) – начальное состояние
S = S1 × S2 × … × Sn – пространство стратегий
u = u1 × … × un,- функция полезности, где
ui: Θ(ℍ) → ℜ для игрока i

орлом вверх
Q либо переворачивает ее (F), либо нет (N)
затем

P либо переворачивает монету (F) либо нет (N)
и наконец Q делает финальный ход либо переворачивая монету (F) либо нет (N)
Если в конце монета лежит орлом вверх, то выигрывает P с выигрышем +1, а проигрыш Q составляет -1. В противном случае Q получает +1, а P получает -1.
Матрица выигрышей
Q NN NF FN FF
P:N (−1, +1) (+1, −1) (+1, −1) (−1, +1)
P:F (+1, −1) (−1, +1) (−1, +1) (+1, −1)

Q применяет квантовую стратегию
P обречен на классическую стратегию
|0〉 - орел
|1〉 - решка
состояние игры представляется кубитом ψ = α|0〉 + β|1〉
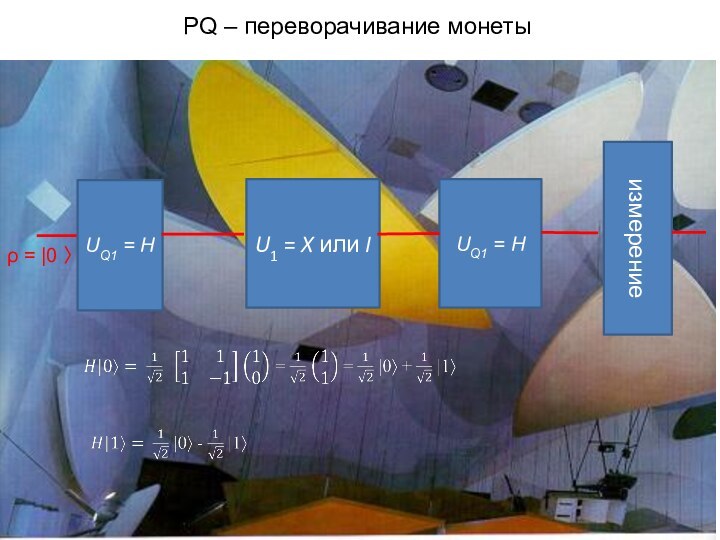
начальное состояние игры ρ = |0 〉
первый ход – тождественное преобразование U
переворачивание F и непереворачивание N представляются преобразованиями X и I соответственно
P может сыграть либо X, либо I, а Q может выбрать любое унитарное преобразование (используется преобразование Адамара)
игра характеризуется как
G(n = 2,Θ(ℍ) = ℍ,ρ = |0 〉,S1×S2,,u)
S1 = {X,I}, S2 есть множество всех унитарных матриц
U совпадает с классическим случаем

или I
UQ1 = H
измерение
ρ = |0 〉

 
 

⊗3ℍ
T(1,1,1)(|x〉⊗|y〉⊗|z〉) = |x〉⊗|y〉⊗|min(x,y)⊗z〉
Q(1,1,1): ⊗3ℍ → ⊗3ℍ
Q(1,1,1)(|x〉⊗|y〉⊗|z〉) = |x〉⊗|y〉⊗|max(x,y)⊗z〉
AND(|ϕ〉,|ψ〉)

= T(1,1,1)(|ϕ〉⊗|ψ〉⊗|0〉)
NOT(|ϕ〉) = T(1,1,1)(|ϕ〉⊗|1〉⊗|1〉)
OR(|ϕ〉,|ψ〉) = Q(1,1,1)(|ϕ〉⊗|ψ〉⊗|0〉)

 

Аксиоматизируема ли QCL?

в исчисление Лукасевича Łℵ0 и построил модальное расширение логики,

обогатив систему модальным символом Q и четырьмя модальными правилами вывода. Высказывание QА при этом означает «А подтверждается экспериментом», а наиболее специфическое правило вывода можно сформулировать так: для совместных измерений импликация эквивалентна подтверждению материальной импликации.

интерпретация, если она удовлетворяет следующим условиям:
(I) I(A → B)

= min(1,1−I(A)+I(B));
(II) I(¬A) = 1−I(A);
(III) I(QA) = q(I(A));
для любых A,B∈W0, где W0 – множество формул ŁQ.
При этом 1:ψ→{1} , где ψ - множество всех состояний объекта, причем состояние, как обычно, представляет собой вектор гильбертова пространства, а любая функция g: ψ → [0,1] называется обобщенным вопросом. Далее, P ⊆ S, где S - множество всех обобщенных вопросов, а P − множество обычных квантовологических вопросов («да-нет»-измерений), и функция q: S → P определяется условиями:
a1. g ≤ h ⇒ q(g) ≤ q(h);
a2. q(p) = p;
для любых g,h∈S; p∈P.
Очевидным образом при таком определении для модальных формул ŁQ функция q играет ту же роль, что и функция p у Макки, ставящая в соответствие каждой тройке (A,α,E) (где A∈A, α∈S, E∈B; A − множество наблюдаемых, S - множество состояний, В – множество всех борелевских подмножеств действительной числовой прямой) число p(A,α,E), 0 ≤ p(A,α,E) ≤ 1. Роль множества наблюдаемых выполняет W0, множества состояний – dom(S), множества B – rng(S).

(A → B) → ((B → C) → (A

→ C))
A3. ((A → B) → B) → ((B → A) → A)
A4. (¬A → ¬B) → (B → A)
B5. A, A → B
B
B6. A
QA
B7. A
¬Q¬A
B8. A → B
QA → QB
B9. QA → QB
(QB → QA) ↔ Q(QB ⊃ QA)
D4. A ⊃ B = def ¬A ∨ B

К приведенным аксиомам может быть добавлена еще одна:

A10. QA ↔ ¬Q¬A

множество, O∈K,
R - тернарное отношение
достижимости на K

и * - унарная операция на K.
p1. ROaa
p2. Raaa
p3. R2abcd ⇒ R2acbd
p4. R2Oabc ⇒ Rabc
p5. Rabc ⇒ Rac*b*
p6. a** = a
p7. ROab ∨ ROb
d1. a < b =def Roab
d2. R2abcd =def
∃x(Rabx & Rxcd & x∈K)

v есть оценка в Ł-фрейме, т.е. v является функцией ν:S×K→S[0,1] (S есть множество пропозициональных переменных и S[0,1] есть обычная логическая матрица для Łℵ0,), которая для всякого p∈S и всяких a,b∈K удовлетворяет следующему условию:
(1) a < b & v(p,a) ≠ 0 ⇒ v(p,b) ≠ 0;

I есть интерпретация, ассоциированная с v, т.е. I есть функция I: F×K → S[0,1] (F есть множество формул), удовлетворяющая ⎯ для всякого p∈S, всяких A,B∈F и всякого a∈K ⎯ следующим условиям:
I(p,a) = v(p,a);
I(¬A,a) = 1-x тогда и только тогда, когда I(A,a*) = x;
I(A→B,a) = min(1,1−x+y) тогда и только тогда, когда для всяких b,c∈K Rabc и I(A,b) = x ⇒ I(B,c) = y.
I(QA,a) = inf{I(A,c) : for any b∈K(ROab) ⇒ c∈K(R0bc ⇒ I(A,c) ≠ 0)}

→ B в точке a, то всякий раз как

2й игрок пытается опровергнуть это утверждение, полагая A в точке b, 1й должен также принимать B в точке c, где точки выбираются согласно приведенным ранее условиям. (И наоборот, т.е. когда 1й и 2й меняются ролями.)

(R¬) Если 1й игрок принимает ¬A в точке a, то 2й игрок пытается опровергнуть это утверждение, полагая A точке a* где точки выбираются согласно приведенным ранее условиям. (И наоборот, т.е. когда 1й и 2й меняются ролями.)

(RQ) Если 1й игрок принимает QA, то 1й игрок также должен принимать A (его интерпретация должна быть отлична от 0) в любой точке, которую 2й игрок может выбрать, используя приведенные ранее условия. И наоборот, т.е. когда 1й и 2й меняются ролями.)