Презентация на тему логические операции и таблицы истинности

Содержание

2. Таблица истинности — это таблица, устанавливающая соответствие
3. При построении таблиц истинности есть определенная последовательность
4. Необходимо построить таблицу истинности с
5. Равносильные логические выражения Логические выражения, у которых
6. Пример. Построить таблицу истинности для составного высказывания:Количество
7. 3. Строим таблицу с указанным количеством
9. Скачать презентацию
10. Похожие презентации

Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.

Главная
Информатика
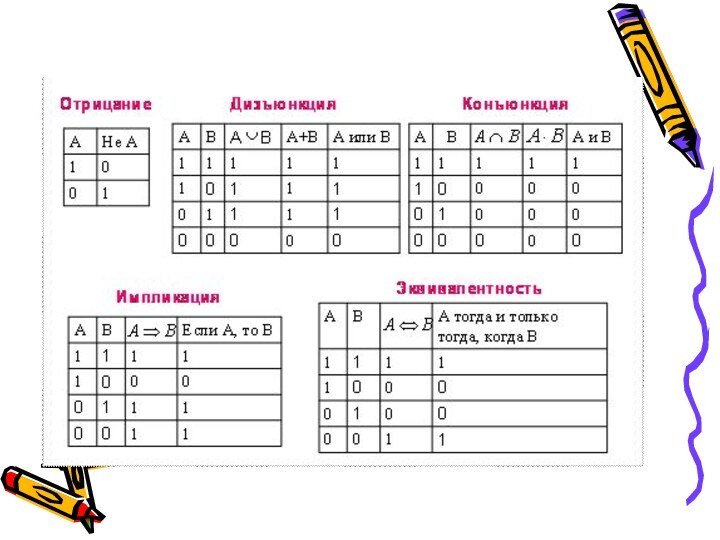
логические операции и таблицы истинности

Логические выражения и таблицы истинностиИванова Юлия

Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических

При построении таблиц истинности есть определенная последовательность действий: Необходимо определить количество строк

Необходимо построить таблицу истинности с указанным количеством строк и столбцов,

Равносильные логические выражения Логические выражения, у которых последние столбцы таблиц истинности совпадают,

Пример. Построить таблицу истинности для составного высказывания:Количество строк в таблице:

3. Строим таблицу с указанным количеством строк и столбцов. Обозначаем столбцы

логические операции и таблицы истинности

Слайды презентации

Слайд 2 Таблица истинности — это таблица, устанавливающая соответствие между

Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений

возможными наборами значений логических переменных и значениями функций.

Слайд 3 При построении таблиц истинности есть определенная последовательность действий:

При построении таблиц истинности есть определенная последовательность действий: Необходимо определить количество

Необходимо определить количество строк в таблице истинности: количество строк

равно где n — количество логических переменных.
Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

Слайд 4
Необходимо построить таблицу истинности с указанным

количеством строк и столбцов, ввести названия столбцов таблицы в

соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
Заполнить столбцы входных переменных наборами значений;
Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Пример

Слайд 5 Равносильные логические выражения
Логические выражения, у которых последние

Равносильные логические выражения Логические выражения, у которых последние столбцы таблиц истинности

столбцы таблиц истинности совпадают, называются равносильными.
Для обозначения равносильных

логических выражений используется знак “ = “.

Слайд 6 Пример. Построить таблицу истинности для составного высказывания:

Количество строк

в таблице:
Т.к. логическая функция содержит

2 переменные, следовательно количество строк в таблице истинности равно 22=4.
Количество столбцов:
Т.к. количество переменных равно 2, а количество логических операций – 5, то количество столбцов таблицы истинности равно 7.