- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгоритм Forel. Выделение устойчивых таксонов
Содержание
- 2. СодержаниеАлгоритм Forel 2Выделение устойчивых таксоновТаксономия динамически описываемых
- 3. Назначение и свойства алгоритма Forel 2Предназначен для
- 4. Алгоритм FOREL-2 (шаги 1-5) Шаг 1. Все
- 5. Алгоритм FOREL-2 (шаги 5 - 12) Шаг
- 6. Алгоритм FOREL-2 (шаги 13 - 18) Шаг
- 7. Алгоритм FOREL-2 (шаги 19 - 22)Шаг 19.
- 8. Пример 1Разбить 4 объекта на три таксона,
- 9. Решение задачи примера 124312431
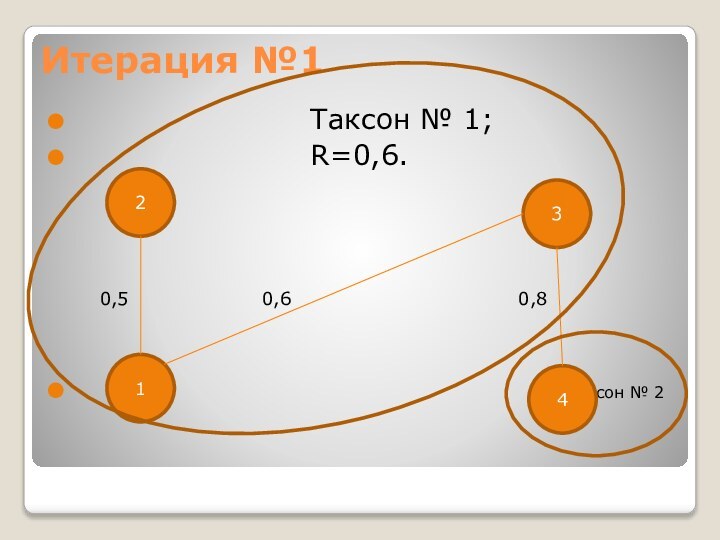
- 10. Итерация №1
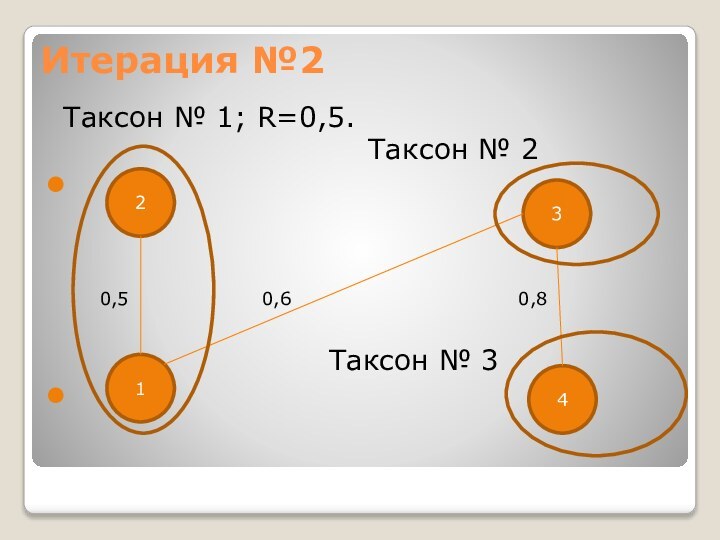
- 11. Итерация №2 Таксон № 1; R=0,5.
- 12. Самостоятельно1. Заполнить матрицу M, имеющую 4 строки
- 13. САМОСТОЯТЕЛЬНООпределить достоинства и недостатки алгоритма Forel 2.
- 14. Алгоритм SkatШаг 1. Определяется таксономия S для
- 15. САМОСТОЯТЕЛЬНОПользуясь алгоритмом SKAT и, в его рамках,
- 16. Решение задачи1) Таксономия S1 при исходной нумерации:
- 17. САМОСТОЯТЕЛЬНООпределите достоинства и недостатки алгоритма SKAT
- 18. САМОСТОЯТЕЛЬНОСоставить блок-схему алгоритма SKAT.Реализовать алгоритм программно.Исследовать созданную
- 19. Динамическая таксономияНиже рассматривается ситуация, когда в ходе
- 20. Алгоритм DINAШаг 1.Ввод R - радиуса таксона.Шаг
- 21. Пример 2 Определить, пользуясь DINA, таксономию трёх
- 22. Таблица исходных данных
- 23. Таблица нормированных данных
- 24. Порядок решенияКруг - центр первого таксона. Расстояние
- 25. ОТВЕТТаксон № 1
- 26. Скачать презентацию
- 27. Похожие презентации
СодержаниеАлгоритм Forel 2Выделение устойчивых таксоновТаксономия динамически описываемых объектов.Выбор алгоритмов таксономии.Пример 1. Примеры прикладных задач таксономии: прогнозирование успеваемости;ранжирование объектов.























Слайд 2
Содержание
Алгоритм Forel 2
Выделение устойчивых таксонов
Таксономия динамически описываемых объектов.
Выбор
алгоритмов таксономии.
объектов.
Слайд 3
Назначение и свойства алгоритма Forel 2
Предназначен для группировки
объектов в таких условиях, когда:
все характеристики объектов однородны,
число
таксонов N задано,обладает таксонами, которые имеют форму гиперсферы.
Слайд 4
Алгоритм FOREL-2 (шаги 1-5)
Шаг 1. Все признаки объектов
нормируются так, чтобы их значения были в диапазоне 0
- 1.Шаг 2. R0=+∞
Шаг 3. Все точки считаем непомеченными.
Шаг 4. На множестве непомеченных точек выбирается произвольная xi, после чего осуществляется переход к шагу 5. Если таковых точек нет, то перейти к шагу 8.
Шаг 5. Ищется максимальное расстояние R от xi до остальных точек.
Слайд 5
Алгоритм FOREL-2 (шаги 5 - 12)
Шаг 6. R0
= min {R0;R} .
Шаг 7. Точка xi помечается. Если
помечены все точки, то перейти к шагу 8, нет - к шагу 4.Шаг 8. R=R0-ε
Шаг 9. Если множество точек пусто, то перейти к шагу 16, нет - к шагу 10.
Шаг 10. Все точки считаем непомеченными.
Шаг 11. На множестве непомеченных точек выбирается произвольная точка xi.
Шаг 12. Определяется число точек P(xi), расстояние которых до xi не превышает R.
Слайд 6
Алгоритм FOREL-2 (шаги 13 - 18)
Шаг 13.
Точку xi считаем помеченной. Если помечены все точки, то
перейти к шагу 14, нет - к шагу 11.Шаг 14. Выбирается j-я точка , для которой справедливо: P(xi)≤P(xj), i=1,2,3,…n.
Шаг 15. Все точки, расстояние от которых до не превышает R, удаляются. Перейти к шагу 9.
Шаг 16. Если число таксонов меньше N, то перейти к шагу 17, иначе к шагу 19.
Шаг 17. R=R-ε .
Шаг 18. Все точки возвращаются на «свои места», перейти к шагу 10.
Слайд 7
Алгоритм FOREL-2 (шаги 19 - 22)
Шаг 19. Если
число таксонов равно N, то перейти к шагу 22,
нет - к шагу 20.Шаг 20. ε=ε/2.
Шаг 21. R=R+ε, перейти к шагу 18.
Шаг 22. Конец алгоритма.
Слайд 8
Пример 1
Разбить 4 объекта на три таксона, если
λ-расстояния между объектами приведены ниже в таблице М, ε
= 0,1.М=
Слайд 12
Самостоятельно
1. Заполнить матрицу M, имеющую 4 строки и
два столбца:
где k – порядковый номер студента.
2. Полагая, что строки отвечают объектам, а столбцы – критериям, выделить, пользуясь Forel 1, таксоны при условии, что Ɛ = 0,5.
3. Разбить все объекты на 3 таксона, пользуясь Forel 2.
Слайд 14
Алгоритм Skat
Шаг 1. Определяется таксономия S для m
объектов с помощью FOREL-1.
Шаг 2. Используя центры таксонов в
S, как новые стартовые точки для FOREL-1, определяются таксономии S1,S2,…Sn.Шаг 3. Выбор устойчивых таксонов.
Шаг 4. Конец алгоритма.
Слайд 15
САМОСТОЯТЕЛЬНО
Пользуясь алгоритмом SKAT и, в его рамках, алгоритмом
FOREL 1, выделить устойчивые таксоны в таблице:
Слайд 16
Решение задачи
1) Таксономия S1 при исходной нумерации:
1-й таксон: 1, 2; 2-й таксон: 3.
2)
Таксономия S2 при обратной нумерации объектов (строк):1-й таксон: 2, 3; 2-й таксон: 1.
3) Вывод: таксоны неустойчивы.
Слайд 18
САМОСТОЯТЕЛЬНО
Составить блок-схему алгоритма SKAT.
Реализовать алгоритм программно.
Исследовать созданную программу,
построив график зависимости времени счета от размерности исходной матрицы.
Слайд 19
Динамическая таксономия
Ниже рассматривается ситуация, когда в ходе исследований
объекты возникают по одному или группами и на каждой
итерации осуществляется таксономия. В этом случае используется алгоритм DINA, описание которого приводится ниже.
Слайд 20
Алгоритм DINA
Шаг 1.Ввод R - радиуса таксона.
Шаг 2.
i=1.
Шаг 3. Ввод i-го объекта.
Шаг 4. Если i>1, то
перейти к шагу 6.Шаг 5. Введённый объект отвечает центру первого таксона.
Шаг 6. Определяется расстояние от i-й точки до центров всех созданных таксонов.
Шаг 7. Если кратчайшее из этих расстояний меньше R, то i-й объект принадлежит соответствующему таксону, в противном случае i-й объект - центр нового таксона.
Шаг 8. i=i+1.
Шаг 9. Если ввод объектов завершён, то перейти к шагу 10, нет - к шагу 3.
Шаг 10. Конец алгоритма.
Слайд 21
Пример 2
Определить, пользуясь DINA, таксономию трёх последовательно
возникающих объектов: круга, квадрата и треугольника, характеризующихся Таблицей, представленной
на следующем слайде, R=1.
Слайд 24
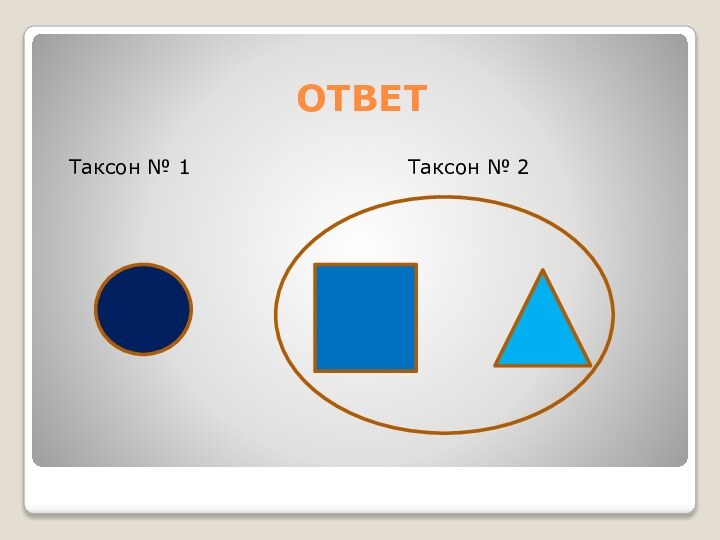
Порядок решения
Круг - центр первого таксона. Расстояние между
квадратом и кругом больше R: r1=1.1657, следовательно квадрат -
центр второго таксона.Расстояние между треугольником и квадратом r2=0.7541 меньше, чем между треугольником и кругом r3=1.013422 и меньше R, следовательно треугольник принадлежит ко второму таксону.





























