- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Генерация случайных чисел
Содержание
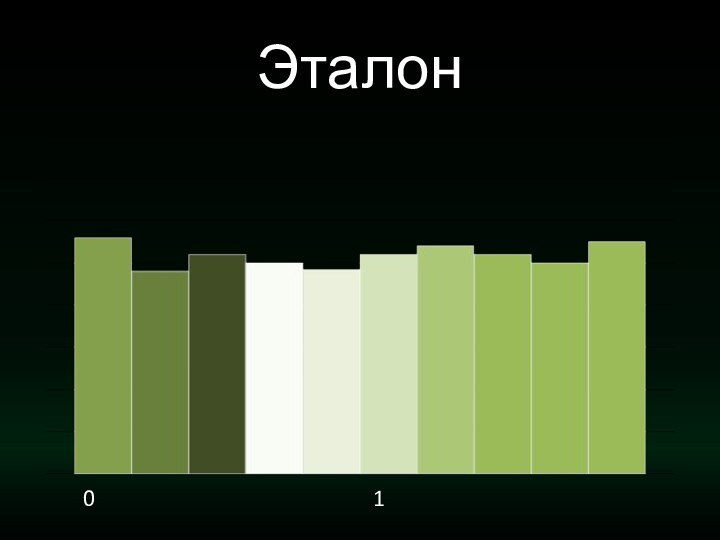
- 2. Эталон0 1
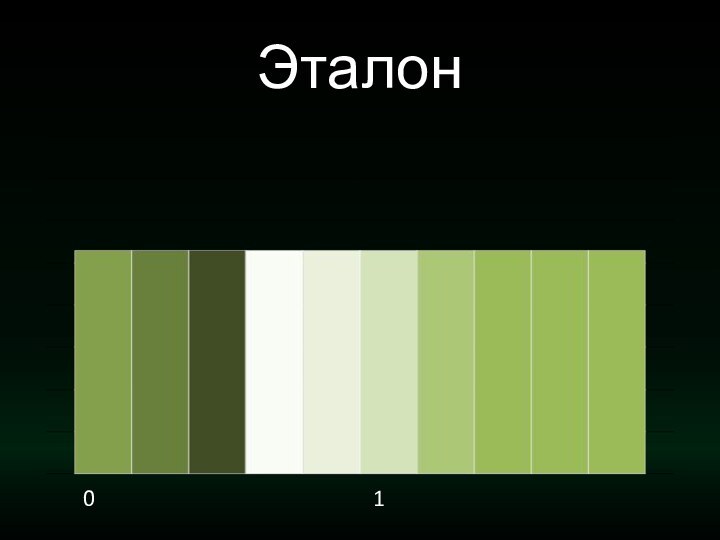
- 3. Эталон0 1
- 4. Генераторы
- 5. Генераторыфизические
- 6. Генераторыфизическиетабличные
- 7. Генераторыфизическиетабличныеалгоритмические
- 8. Первые алгоритмы«Всякий, кто питает слабость к арифметическим
- 9. Первые алгоритмыМетод серединных квадратов
- 10. Первые алгоритмыМетод серединных квадратов
- 11. Первые алгоритмыМетод серединных квадратов
- 12. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийR0 × R1
- 13. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийR0 × R1
- 14. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийR0 ×
- 15. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийМетод перемешивания
- 16. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийМетод перемешивания3456781256781234
- 17. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийМетод перемешивания345678125678123412345678
- 18. Первые алгоритмыМетод серединных квадратовМетод серединных произведенийМетод перемешивания345678125678123412345678+
- 19. Линейная конгруэнция
- 20. Линейная конгруэнцияRi+1 = (K * Ri + B) % M
- 21. Линейная конгруэнцияRi+1 = (K * Ri + B) % MB и M взаимно простые
- 22. Линейная конгруэнцияRi+1 = (K * Ri +
- 23. Линейная конгруэнцияRi+1 = (K * Ri +
- 24. Датчик Фибоначчи
- 25. Датчик ФибоначчиRi = Ri - a – Ri - b
- 26. Датчик ФибоначчиRi = Ri - a – Ri - ba, b – лаги
- 27. Датчик ФибоначчиRi = Ri - a – Ri - ba, b – лагициклическая очередь значений
- 28. Датчик ФибоначчиRi = Ri - a –
- 29. LFSR
- 30. LFSRRi = (c1 × Ri-1) ⊕ (c2
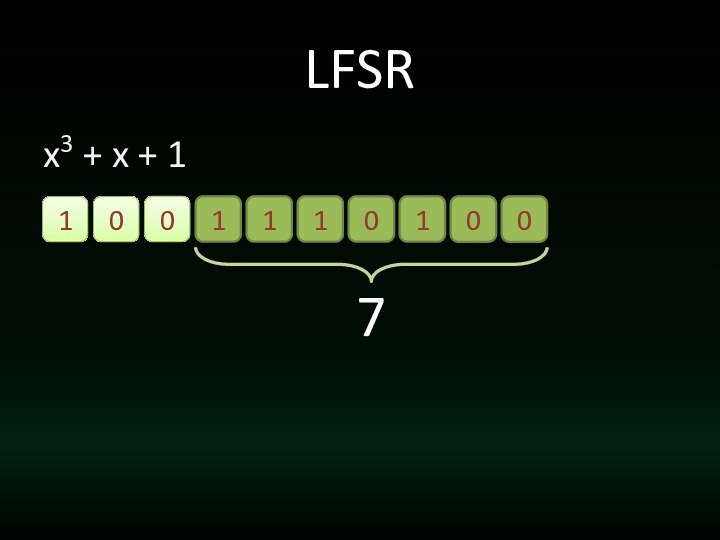
- 31. LFSRx3 + x + 1010111010011101007
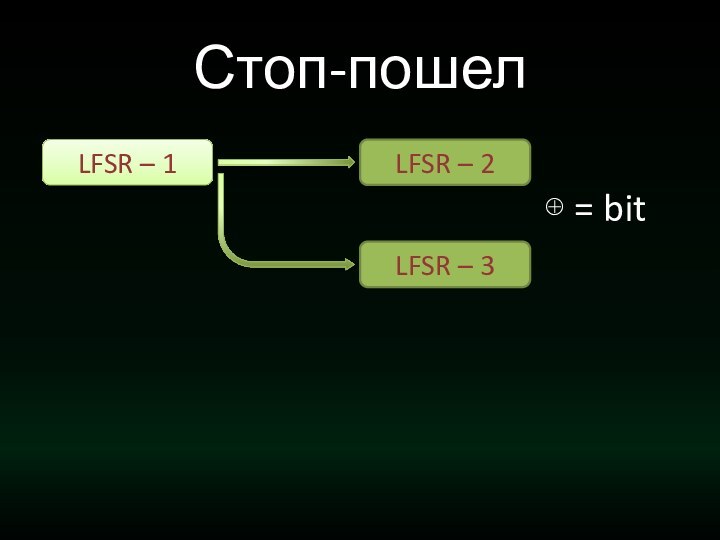
- 32. Стоп-пошелLFSR – 1LFSR – 2LFSR – 3⊕ = bit
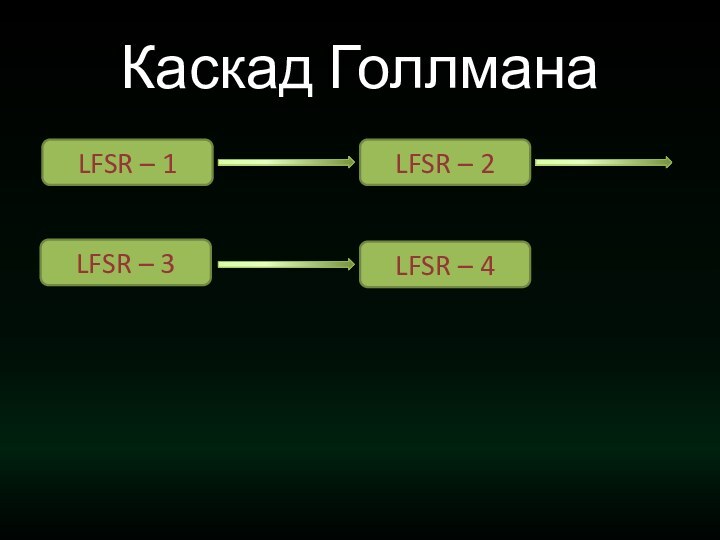
- 33. Каскад ГоллманаLFSR – 1LFSR – 2LFSR – 3LFSR – 4
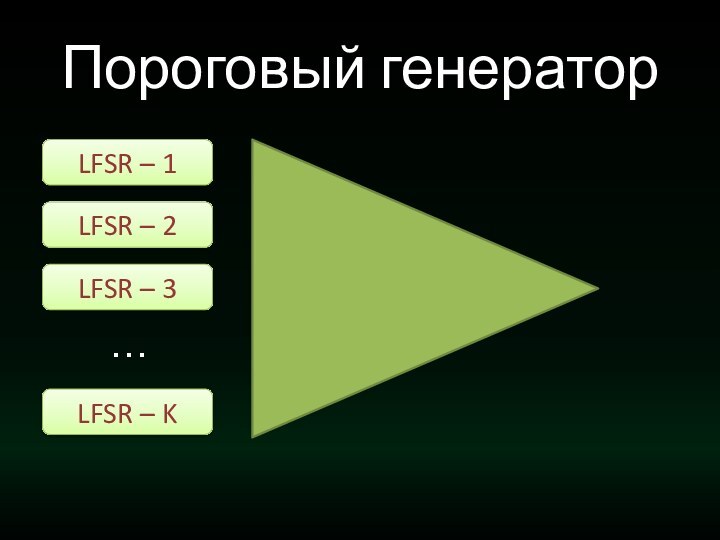
- 34. Пороговый генераторLFSR – 1LFSR – 2LFSR – 3LFSR – K…
- 35. Тестирование
- 36. ТестированиеNISTDIEHARDpLab ProjectCRYPT-XTEST-U01DieharderENTKnuth’s
- 37. ТестированиеNISTDIEHARDpLab ProjectCRYPT-XTEST-U01DieharderENTKnuth’s
- 38. NIST
- 39. NISTЧастотный побитовый тест
- 40. NISTЧастотный побитовый тестЧастотный блочный тест
- 41. NISTЧастотный побитовый тестЧастотный блочный тестПоследовательность одинаковых бит
- 42. NISTЧастотный побитовый тестЧастотный блочный тестПоследовательность одинаковых битСамая длинная последовательность единиц в блоке
- 43. NISTРанговый тест
- 44. NISTРанговый тестСпектральный тест
- 45. NISTРанговый тестСпектральный тестТест на шаблоны
- 46. NISTРанговый тестСпектральный тестТест на шаблоныТест на пересекающиеся шаблоны
- 47. NISTРанговый тестСпектральный тестТест на шаблоныТест на пересекающиеся шаблоныТест Маурера
- 48. NISTТест на линейную сложность
- 49. NISTТест на линейную сложностьТест на периодичность
- 50. NISTТест на линейную сложностьТест на периодичностьТест приблизительной энтропии
- 51. NISTТест на линейную сложностьТест на периодичностьТест приблизительной энтропииТест кумулятивных сумм
- 52. DIEHARD
- 53. DIEHARDТест на парковку
- 54. DIEHARDТест на парковкуТест сжатия
- 55. DIEHARDТест на парковкуТест сжатияТест игры в кости
- 56. Криптостойкость
- 57. КриптостойкостьГенерация ключей
- 58. КриптостойкостьГенерация ключейОдноразовые случайные числа
- 59. КриптостойкостьГенерация ключейОдноразовые случайные числаОдноразовые шифроблокноты
- 60. КриптостойкостьГенерация ключейОдноразовые случайные числаОдноразовые шифроблокнотыГенерация соли
- 61. КриптостойкостьТест на следующий бит
- 62. КриптостойкостьТест на следующий битНа основе блочного шифра
- 63. КриптостойкостьТест на следующий битНа основе блочного шифраНа основе хеш-функции
- 64. КриптостойкостьТест на следующий битНа основе блочного шифраНа
- 65. КриптостойкостьТест на следующий битНа основе блочного шифраНа
- 66. Аппаратные генераторы
- 67. Аппаратные генераторыLavarand
- 68. Аппаратные генераторыLavarandЧипы в процессоре (3 Гб/сек)
- 69. ПО
- 70. ПОgLib – вихрь Мерсена
- 71. ПОgLib – вихрь МерсенаJava – Random, SecureRandom
- 72. ПОgLib – вихрь МерсенаJava – Random, SecureRandomC# - Random, Cryptography.RNG
- 73. ПОgLib – вихрь МерсенаJava – Random, SecureRandomC# - Random, Cryptography.RNGRFC 1750
- 74. Скачать презентацию
- 75. Похожие презентации
Эталон0 1



































































Слайд 8
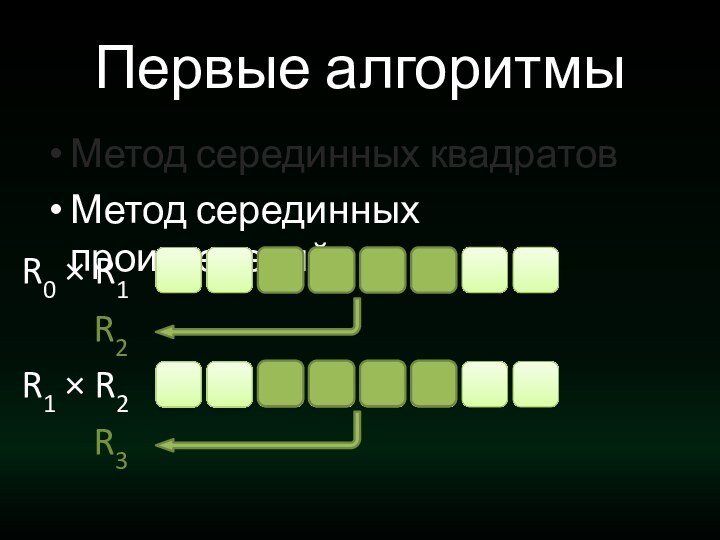
Первые алгоритмы
«Всякий, кто питает слабость к арифметическим методам
получения случайных чисел, грешен вне всяких сомнений»
Слайд 14
Первые алгоритмы
Метод серединных квадратов
Метод серединных произведений
R0 × R1
R2
R1 × R2
R3
Слайд 16
Первые алгоритмы
Метод серединных квадратов
Метод серединных произведений
Метод перемешивания
3
4
5
6
7
8
1
2
5
6
7
8
1
2
3
4
Слайд 17
Первые алгоритмы
Метод серединных квадратов
Метод серединных произведений
Метод перемешивания
3
4
5
6
7
8
1
2
5
6
7
8
1
2
3
4
1
2
3
4
5
6
7
8
Слайд 18
Первые алгоритмы
Метод серединных квадратов
Метод серединных произведений
Метод перемешивания
3
4
5
6
7
8
1
2
5
6
7
8
1
2
3
4
1
2
3
4
5
6
7
8
+
Слайд 22
Линейная конгруэнция
Ri+1 = (K * Ri + B)
% M
B и M – взаимно простые
K – 1
кратно любому простому
делителю M
Слайд 23
Линейная конгруэнция
Ri+1 = (K * Ri + B)
% M
B и M – взаимно простые
K – 1
кратно любому простому
делителю MK – 1 кратно 4, если М кратно 4