- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логика и логические основы компьютера
Содержание
- 2. Содержание Логика, как наука Алгебра высказываний Логические
- 3. Логика-это наука о формах и способах мышления. Мышление
- 4. Алгебра высказываний В алгебре высказываний высказывания обозначаются именами
- 5. Логическое умножение (конъюнкция)Объединение двух (или нескольких) высказываний
- 6. Логическое сложение (дизъюнкция)Объединение двух (или нескольких) высказываний
- 7. Логическое отрицание(инверсия)Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией. F = -A
- 8. Логическое следование(импликация)Логическое следование (импликация) образуется соединением двух
- 9. Логическое равенство(эквивалентность)Логическое равенство (эквивалентность) образуется соединением двух
- 10. Таблицы истинностиТаблица истинности логической функции F = (A v B)&(-A v -B)
- 11. Логические функции
- 12. Логические законыЗакон тождества: А = АЗакон непротиворечия:
- 13. Логические основыустройства компьтераПолусумматор двоичных чисел Полный одноразрядный сумматор Триггер
- 14. Полусумматор двоичных чиселa; b – слагаемыеP – переносS - сумма
- 15. Полный одноразрядный сумматор
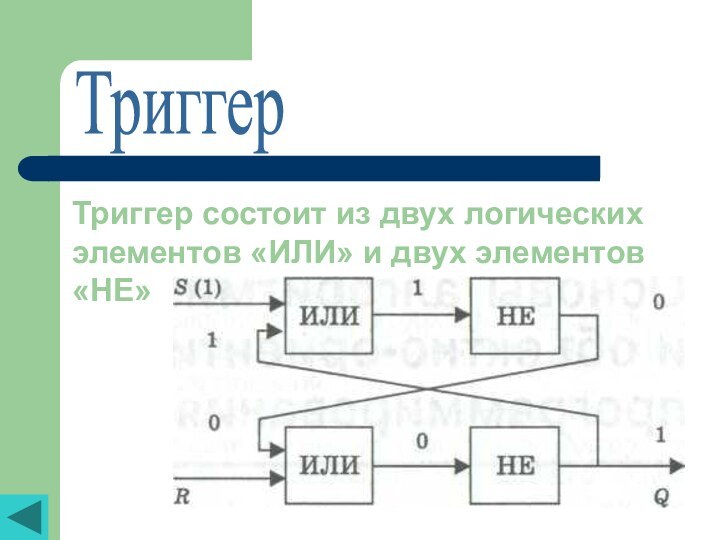
- 16. ТриггерТриггер состоит из двух логических элементов «ИЛИ» и двух элементов «НЕ»
- 17. Скачать презентацию
- 18. Похожие презентации
Содержание Логика, как наука Алгебра высказываний Логические операции: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность Логические законы Логические основы устройства компьютера
















Слайд 2
Содержание
Логика, как наука
Алгебра высказываний
Логические операции:
конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность
устройства компьютера
Слайд 3
Логика
-это наука о формах и способах мышления.
Мышление всегда
осуществляется в каких-то формах. Основными формами мышления являются понятие,
высказывание и умозаключение.
Слайд 4
Алгебра высказываний
В алгебре высказываний высказывания обозначаются именами логических
переменных, которые могут принимать лишь два значения: «истина» (1)
и «ложь» (0).
Слайд 5
Логическое умножение
(конъюнкция)
Объединение двух (или нескольких) высказываний в
одно с помощью союза «и» называется операцией логического умножения
или конъюнкцией, обозначается значком «&» либо «^».F = A & B
Слайд 6
Логическое сложение
(дизъюнкция)
Объединение двух (или нескольких) высказываний с
помощью союза «или» называется операцией логического сложения или дизъюнкцией,
обозначается значком «v» либо «+».F = A v B
Слайд 7
Логическое отрицание
(инверсия)
Присоединение частицы «не» к высказыванию называется операцией
логического отрицания или инверсией.
F = -A
Слайд 8
Логическое следование
(импликация)
Логическое следование (импликация) образуется соединением двух высказываний
в одно с помощью оборота речи «если…, то…».
A
B
Слайд 9
Логическое равенство
(эквивалентность)
Логическое равенство (эквивалентность) образуется соединением двух высказываний
в одно с помощью оборота речи «…тогда и только
тогда, когда…».A ~ B
Слайд 12
Логические законы
Закон тождества: А = А
Закон непротиворечия: А
& -А = 0
Закон исключения третьего: А v -А
= 1Закон двойного отрицания: --А = А
Закон коммутативности: A & B = B & A
Закон ассоциативности: (A&B)&C=A&(B&C)
Закон дистрибутивности:
(A & B )v( A & C)=A&( B v C)





























