- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические основы информатики
Содержание
- 2. Для обработки данных с помощью
- 3. Для автоматизации работы с данными унифицируют форму
- 4. В более узком смысле под кодированием понимается
- 5. При кодировании информации ставятся следующие цели: 1)
- 6. Кодирование данных двоичным кодомДвоичное кодирование- представление данных
- 7. В качестве эталона меры измерения информации выбран
- 8. Единицы измерения данных1Мбайт = 1024 Кбайт =
- 9. Кодирование данных двоичным кодом00 01 10 11000
- 10. СИСТЕМЫ СЧИСЛЕНИЯ Системой счисления называется совокупность приемов
- 11. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Система счисления называется позиционной,
- 12. Десятичная позиционная система счисления основана на том,
- 13. Число К единиц какого-либо разряда, объединяемых в
- 14. Системы счисления:10 (десячичная): 0,1,2,3,4,5....9
- 15. 10 0 1 2
- 16. Правила перевода из одной системы счисления в другую
- 17. 1) Из 10 в 2Исходное число в
- 18. 123 122 12 61
- 19. 123 112 1116 7
- 20. 2) 2, 16 в 10Исходное число раскрывается
- 21. 1111011 = 1*2 +1*2 +1*2 +1*2 +0*2
- 22. 3) 2 в 16 и 16 в
- 23. 10 0 1 2
- 24. 7B =011110110001 1011 1011 = 1BB1BB162216
- 25. Арифметические действия над числами в любой позиционной
- 26. ДВОИЧНАЯ АРИФМЕТИКА
- 27. +A 0 0 1
- 28. -A 0 0 1
- 29. *A 0 0 1
- 30. A 0 0 1
- 31. :1011 11 11
- 32. Кодирование целых чисел:От 0 до 255 -
- 33. Для кодирования действительных чисел используют 80-разрядное кодирование.
- 34. При этом число предварительно преобразуется в
- 35. 0,123456789*10МантиссаХарактеристика
- 36. Кодирование текстовых данныхДвоичных код используют при кодировании текста, когда каждому символу алфавита сопоставляется определенное число.
- 37. Кодирование текстовых данных:При кодировании текстовой информации
- 38. UNICODE - универсальная система кодирования, основанная
- 39. Кодирование графических данных:Для кодирования графических данных
- 40. Скачать презентацию
- 41. Похожие презентации
Для обработки данных с помощью средств вычислительной техники они должны быть преобразованы в понятную для ЭВМ форму.

















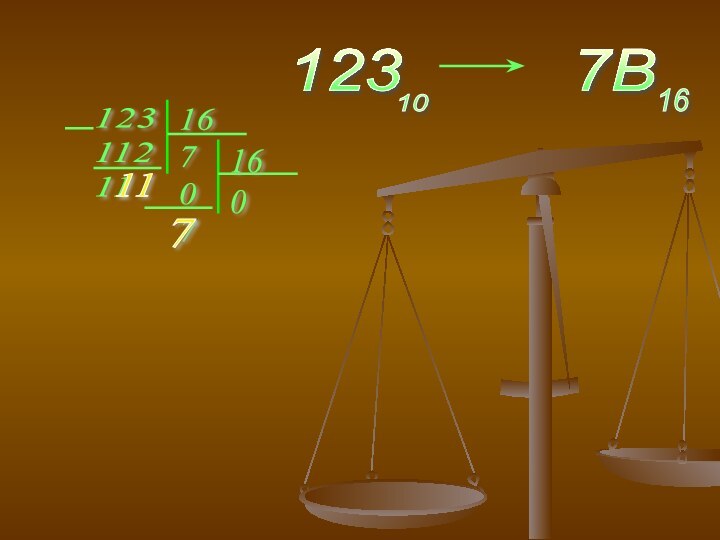

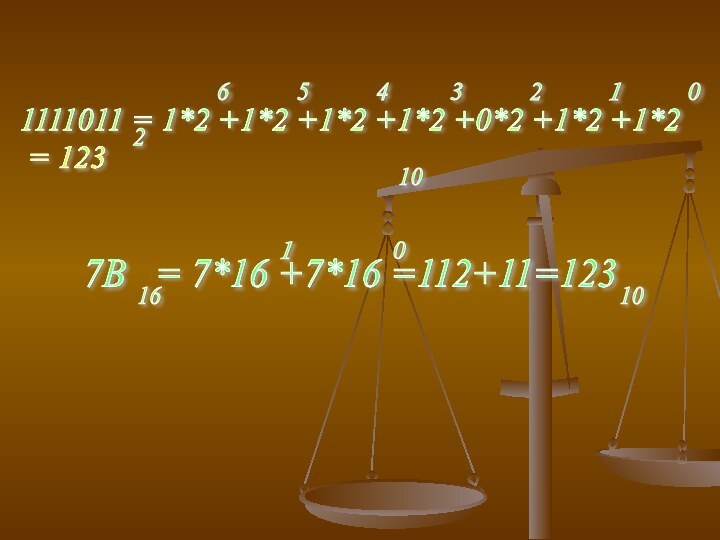

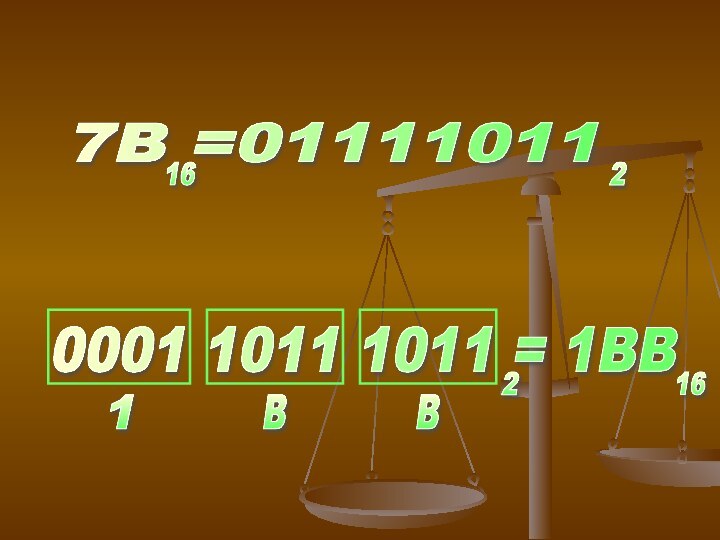
















Слайд 3
Для автоматизации работы с данными унифицируют форму представления
данных – применяют кодирование
Кодирование- выражение данных одного типа через
данные другого типа.
Слайд 4
В более узком смысле под кодированием понимается переход
от исходного представления информации, удобного для восприятия человеком, к
представлению, удобному для хранения, передачи и обработки.Обратный переход к исходному представлению называется декодированием.
Слайд 5
При кодировании информации ставятся следующие цели:
1) удобство
физической реализации;
2) удобство восприятия;
3) высокая скорость передачи и обработки;
4)
экономичность, т.е. уменьшение избыточности сообщения;5) надежность, т.е. зашита от случайных искажений;
6) сохранность, т.е. защита от нежелательного доступа к информации.
Слайд 6
Кодирование данных двоичным кодом
Двоичное кодирование- представление данных последовательностью
двух знаков : 0 и 1.
Двоичные цифры – binary
digit – bit (бит)Один бит выражает два понятия: 0 и 1 (да и нет, черное и белое)
Слайд 7 В качестве эталона меры измерения информации выбран абстрактный
объект,
который может находиться в одном из 2-х состояний:
ДА
- НЕТ, ВКЛ.- ВЫКЛ..
Такой объект содержит информацию в 1 БИТ8 бит = 1байт
2 байт = 1 кб
10
Слайд 8
Единицы измерения данных
1Мбайт = 1024 Кбайт = 210
байт
1Гбайт = 1024 Мбайт = 230 байт
1Тбайт = 1024
Гбайт = 210 байт
Слайд 9
Кодирование данных двоичным кодом
00 01 10 11
000 001
010 011 100 101 110 111
Для кодирования целых чисел
от 0 255 достаточно иметь 8 разрядов двоичного кода (8 бит)0000 0000 = 0
0000 0001 = 1
1111 1111 = 255
Слайд 10
СИСТЕМЫ СЧИСЛЕНИЯ
Системой счисления называется совокупность приемов наименования
и записи чисел.
В любой системе счисления для представления чисел
выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.
Слайд 11
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления называется позиционной, если
значение каждой цифры (ее вес) изменяется в зависимости от
ее положения (позиции) в последовательности цифр, изображающих число.
Слайд 12
Десятичная позиционная система счисления
основана на том, что
десять единиц каждого разряда объединяются в одну единицу соседнего
старшего разряда.Таким образом, каждый разряд имеет вес, равный степени 10.
Например, в записи числа 343.32 цифра 3 повторена три раза, при этом самая левая цифра 3 означает количество сотен (ее вес равен 102); цифра 3. стоящая перед точкой, означает количество единиц (ее вес равен 100 ), а самая правая цифра 3 — количество десятых долей единицы (ее вес равен 10-1), так что последовательность цифр 343.32 представляет собой сокращенную запись выражения :
3x102 + 4x101+3x100 + 3x10-1 + 2x10-2.
Десятичная запись любого числа X в виде последовательности цифр:
аnаn-1..а1aоа-1...ат...
основана на представлении этого числа в виде полинома:
Х = аn10n + аn-110n-1+... +a1 101+a0100+a-110-1+...+a-m10-m...,
Слайд 13
Число К единиц какого-либо разряда, объединяемых в единицу
более старшего разряда, называют основанием позиционной системы счисления, а
сама система счисления называется К-ичной.Например, основанием десятичной системы счисления является число 10;
двоичной — число 2;
троичной — число 3 и т.д.
Для записи произвольного числа в K-ичной системе счисления достаточно иметь К разных цифр аi i=1,...K.
Например, в троичной системе счисления любое число может быть выражено посредством цифр 0, 1,2. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
Слайд 14
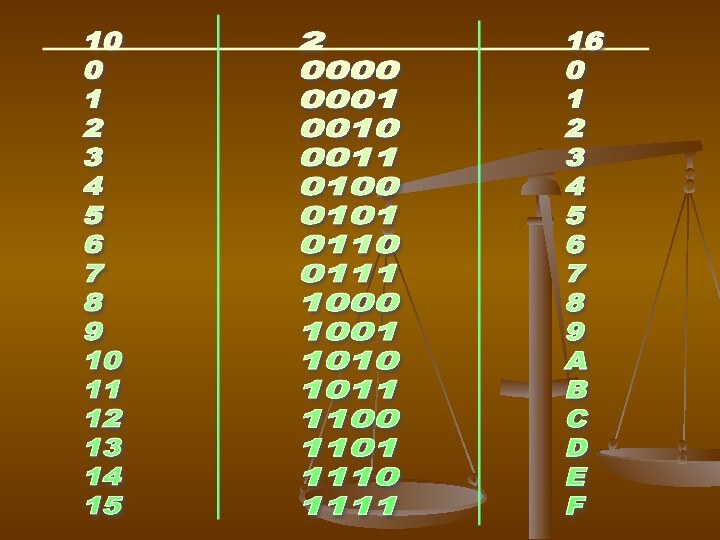
Системы счисления:
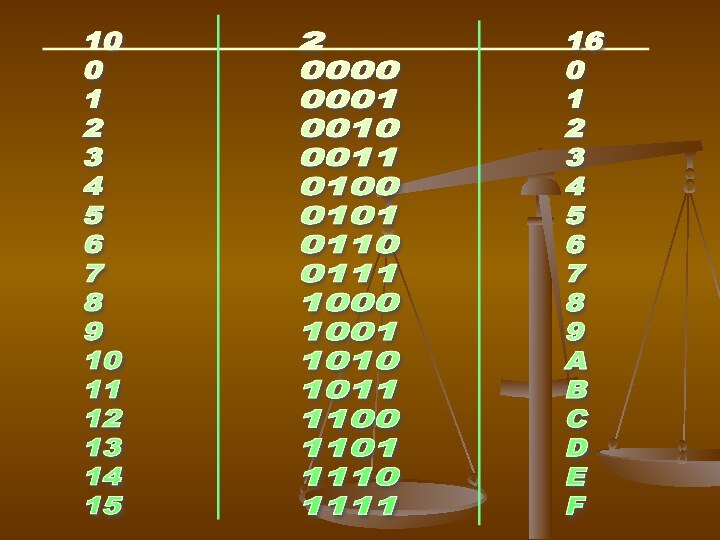
10 (десячичная): 0,1,2,3,4,5....9
2 (двочная): 0,1
16 (шеснадцатиричная): 0...9ABCDEF
Слайд 15 10 0 1 2 3 4 5 6
7
8
9
10
11
12
13
14
15
2
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
111116
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Слайд 17
1) Из 10 в 2
Исходное число в 10
С/С подвергается делению на основание той С/С, в
какую осуществляется перевод.
Слайд 20
2) 2, 16 в 10
Исходное число раскрывается как
сумма n *-ий соответсвующих цифр исходного числа на основание
исходной С/С в нужной степени.Слайд 21 1111011 = 1*2 +1*2 +1*2 +1*2 +0*2 +1*2
+1*2
= 123
2
10
5
6
4
3
2
1
0
7В = 7*16 +7*16 =112+11=123
16
1
0
10
Слайд 22
3) 2 в 16 и 16 в 2
При
переводе 2 в 16 исходное число делится на группу
по 4 цифры в каждой, и к каждой группе в соответствие ставится символ 16 системы.Слайд 23 10 0 1 2 3 4 5 6
7
8
9
10
11
12
13
14
15
2
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
111116
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Слайд 25
Арифметические действия над числами в любой позиционной системе
счисления производятся по тем же правилам, что и в
десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами.При этом нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления.
Слайд 32
Кодирование целых чисел:
От 0 до 255 - 8
бит от 0 до 65535 - 16
бит от 0 до 16,5млн - 24 бита
Слайд 34
При этом число предварительно
преобразуется в
НОРМАЛИЗОВАННУЮ ФОРМУ:
3,1415926
= 0,31415926*10 300000 = 0,3*10 123456789 =
0,123456789*101
6
10
Слайд 36
Кодирование текстовых данных
Двоичных код используют при кодировании текста,
когда каждому символу алфавита сопоставляется определенное число.
Слайд 37
Кодирование текстовых данных:
При кодировании текстовой информации
каждому символу
соответствует
определенный код
1 буква - 8 разрядов
0 -
31 (первые 32) - управляющие коды
32 - 127 - английский алфавит, цифры, знаки препинания. (ASCII)
128 - 255 - расширенная часть (национальная система кодирования) Слайд 38 UNICODE - универсальная система кодирования, основанная на 16-разрядном
кодировании символов, позволяющих обеспечить уникальные коды для 65
536 различных символов.
Слайд 39
Кодирование графических данных:
Для кодирования графических данных
применяется принцип
декомпозиции; производные цвета зеленый, красный, синий (RGB) Для каждого
состовляющего - 8разр.=> => для каждой точки - 24 разр.Обеспечивается 16,5 млн. цветов
(TRUE COLOR) ПОЛНОЦВЕТНЫЙ
Дополнительные цвета:
Голубой(С), пурпурный(М), желтый(Y), черный(К) (CMYK)