Слайд 2
Введение
1. Достижения в области теории и практики сетей
2.
Проблемы и границы применимости современных сетевых моделей
3. Единые сети
как новый подход в познании объемных и особо сложных систем Выводы Заключение
Список основных источников
"Вкруг стана вьются и трепещут
Прозрачной сетью кружева,
И шелк узорной паутиной
Сквозит …
И все в восторге, в небесах
Пред сей волшебною картиной…"
А.С. Пушкин. Ранние редакции
романа в стихах "Евгений Онегин
Слайд 3
Введение
В любой дисциплине наличие огромного количества участников -
предметов, объектов, субъектов – и их отношений ( взаимодействий
) наводит на мысль, что такое множество ( сеть) взаимодействующих сущностей само обладает некоторыми общими фундаментальными свойствами. Эти сетевые свойства множества, зависят от его структуры, нежели от внутреннего содержания отдельных сущностей. Если в математике структурные свойства изучает теория графов, то на междисциплинарном стыке сложилось новое направление – теория сетей.
Слайд 4
Введение ( продолжение)
Приложения теория сетей находят свое применение
там, где есть сети, т.е. повсюду. примерами значимых и
актуальных сетевых структур являются:
Internet ; WWW ; Сеть госуправления; Экономические сети; Социальные сети ; Сети знаний ;
Партийные сети; Телевизионные сети; Национальные и местные транспортные маршруты ( авиационные, Железнодорожные, водные, метро, автобус трамвай ; Электрические сети ;
Связь ( почтовая, телефонная); Тепловые сети ; Сети водоснабжения и водоотведения;
Торговые сети ; Сети нервной системы; Разведывательные сети ; Террористические сети.
Слайд 5
Введение ( продолжение)
С.П.Капица: «Человечество в настоящее время не
справляется с проблемами управления -от глобальных- управления миром в
целом, управления страной до семейных».
Потенциал юной теории сетей привлекает к себе внимание и ярко реализуется в отдельных дисциплинах, но все еще не использован в полной мере для того, чтобы раздвинуть временные и концептуальные границы и подступиться к надежным и эффективным решениям социально-экономических и биосоциальных задач различных масштабов.
Слайд 6
1. Достижения в области теории и практики сетей
Теория
графов зародилась в момент,
когда Леонард Эйлер (Leonhard Euler),
швейцарский, немецкий и российский
математик, решил доказать, что прохожий
не может обойти Кёнигсберг (современный
Калининград), используя лишь по одному
разу каждый из семи городских мостов.
Ключевой ее вывод – структурные характеристики графов (сетей) определяют потенциальные возможности их использования
Первый пример использования методов современной алгебры в теории приходится на работы физика Густава Кирхгофа (Gustav Robert Kirchhoff), он сформулировал в 1845 году правила (законы Кирхгофа) для расчета напряжения и тока в электрических цепях.
Слайд 7
1. Достижения в области теории и практики сетей
(продолжение)
Венгерский математик Денеш Кёниг (Dénes Kőnig), опубликовал в 1936
г. книгу «Теория конечных и бесконечных графов» - первый учебник в области теории графов
Введение вероятностных методов в теорию графов, особенно в исследованиях Пала Эрдеша (Paul Erdős) и Альфреда Реньи (Alfréd Rényi) об асимптотической вероятности связности графов, породили еще одну ветвь, известную как теория случайных графов,
Слайд 8
1. Достижения в области теории и практики сетей
(продолжение)
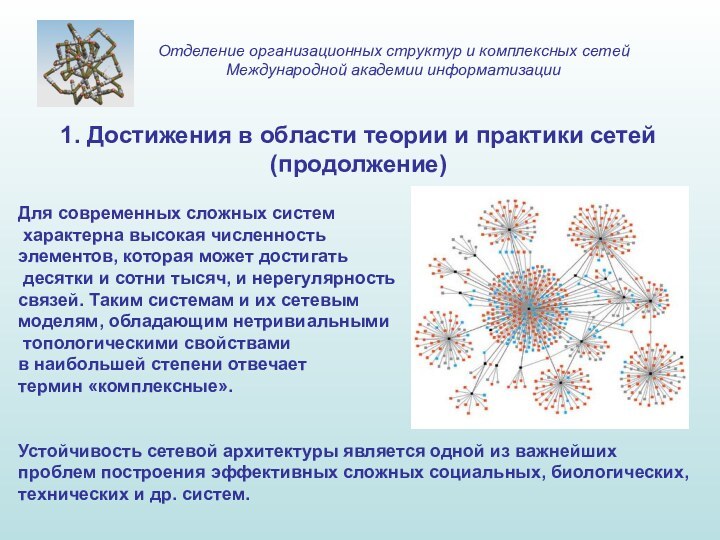
Для современных сложных систем
характерна высокая численность
элементов, которая
может достигать
десятки и сотни тысяч, и нерегулярность
связей. Таким системам и их сетевым
моделям, обладающим нетривиальными
топологическими свойствами
в наибольшей степени отвечает
термин «комплексные».
Устойчивость сетевой архитектуры является одной из важнейших проблем построения эффективных сложных социальных, биологических, технических и др. систем.
Слайд 9
1. Достижения в области теории и практики сетей
(продолжение)
Графическое представление
из [A.-L. Barabási, R. Albert, H. Jeong . Mean-field theory for scale-free random networks . Physica .1999, A 272, P. 173–187 ] обошло весь мир, и широко используется для демонстрации топологии экспоненциальных(а) и безмасштабных (b) сетей.
Слайд 10
2. Проблемы и границы применимости современных сетевых моделей
Сетевые
идеи были уверенно и успешно применены к анализу метаболических
и генетических регуляторных сетей, при разработке надежных масштабируемых сетей проводной и беспроводной связи, для развития стратегии вакцинации в борьбе с болезнями, а также в широком спектре других практических вопросов.
Однако, ни в государственном, ни в корпоративном управлении подобные идеи так и не применялись широко или значимо. Если многие проблемы моделирования организационных структур и межотраслевого управления решены , то вопросы контроля комплексных сетей продолжают оставаться сложными и острыми. Это можно наблюдать на примере обсуждения различных подходов в руководстве Форумом управления глобальной сетью Интернет (IGF)
Слайд 11
2. Проблемы и границы применимости современных сетевых моделей
( продолжение)
Большинство биосоциальных систем характеризуется той или иной степенью
неравенства особей, так что входящие в систему индивиды различаются по (био)социальным рангам; совокупность этих рангов -иерархия, формирует особые отношения и соответствующее сетевое их представление - иерархическое. Иерархические и эгалитарные структуры во многих биосоциальных системах сосуществуют и постоянно взаимодействуют между собой. Часто одна и та же биосоциальная система рассматривается исследователями и практиками в разных ракурсах: в зависимости от предпочтений в фокусе оказывается либо момент иерархичности с доминированием и подчинением, либо наличие в системе уравненных отношений .
Исследователи постоянно сталкиваются с конкурирующей природой сетей и их противопоставлением
Слайд 12
2. Проблемы и границы применимости современных сетевых моделей
( продолжение)
Многие распределенные системы, в частности сети сотовой связи,
компьютерные сети и Интернет, обладают развитой топологией и имеют в своей основе сложные и разнообразные социальные процессы.
По мнению создателя технологии World Wide Web Т. Бернерса Ли (T. Berners-Lee), следующим этапом в развитии Всемирной паутины может стать GGG «Гигантский глобальный граф». Бернерс Ли полагает , что такой граф, в отличие от сети, объединяющей компьютеры, и паутины WWW, связывающей документы, соединит между собой людей и, основываясь на семантических технологиях, предоставит пользователям сервисы более высокого класса, нежели существующие
Слайд 13
3. Единые сети как новый подход
в познании объемных и особо сложных систем
Предложенная А.Тихомировым (Московский государственный университет имени М.В.Ломоносова, РФ) , А.Труфановым ( Иркутский государственный технический университет, РФ) и др. концепция кружева единых сетей КЕС (или ART2 кружево ), базируется на сквозном описании основных категорий взаимодействия множества сущностей ( субъектов, объектов) с помощью многослойного ( многоуровневого ) набора комплексных сетей.
Слайд 14
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
В основе подхода лежат бинарные ( парные) взаимодействия сущностей (акторов) в отдельных тематических слоях (ТС)
Слайд 15
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий, КЕС – множество точек в разных тематических плоскостях и линии соединения в пространстве.
Слайд 16
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Актором кружева единой сети является ствол, стволы крепят узлы сетей различных тематических слоев (ТС)
Слайд 17
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Тематические слои в социальной системе могут определять связи между:
1. родственниками;
2. сокурсниками;
3. работниками одной организации и ведомства- начальниками и подчиненными;
4. коллегами в одной предметной области;
5. соседями и друзьями детства;
6. земляками ;
7. единоверцами
8. друзьями по интересам ;
9. партнерами по бизнесу;
10. случайными знакомыми.
Слайд 18
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
В кружеве допустимо и многоузловое взаимодействие непересекающихся множеств узлов в рассматриваемом ТС ( подобно гиперграфам в теории графов)
Слайд 19
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Если классическом графе не бывает двух различных ребер ( связей) , соединяющих одну и ту же пару вершин (узлов) , то в кружеве число связей , соединяющих пару стволов может быть кратно числу тематических слоев.
Слайд 20
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
При объединении всех ТС в один, ствол вырождается в узел, а единая сеть в комплексную сеть, которая описывается мультиграфом, т.е. графом с кратными ребрами.
Слайд 21
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Как и в случае комплексных сетей, для КЕС ключевыми являются динамические процессы. Динамика социального кружева единых сетей определяется , в первую очередь, динамикой числа стволов -ростом населения Земли.
Слайд 22
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
Новыми метриками, позволяющими оценить дисбаланс формальных и неформальных структур управления обществом, в данной работе предлагаются :
- моменты центральностей M для узла i и центральностей С ( по степени, связи , либо близости) :
L ij - длина пути между узлами i и j, n – число узлов (стволов) в сети;
- узлы тематического слоя t, для которых моменты центральностей имеют минимальные значения в рамках слоя IminC,t ;
Слайд 23
3. Единые сети как новый подход
в познании объемных и особо сложных систем (продолжение)
- перекос t2 в t1:
L IminCt1,jt2 - длина пути между узлами I minCt1 (узел, для которого момент центральность С имеет минимальное значения в рамках слоя t1 и jt2 ( узел слоя t2 ) , t1, t2 t;
- множество (вектор) центральностей для ствола: [Cd, Cb, Cc];
- множество (вектор) моментов центральностей для ствола:[MCd, MCb, MCc];
Слайд 24
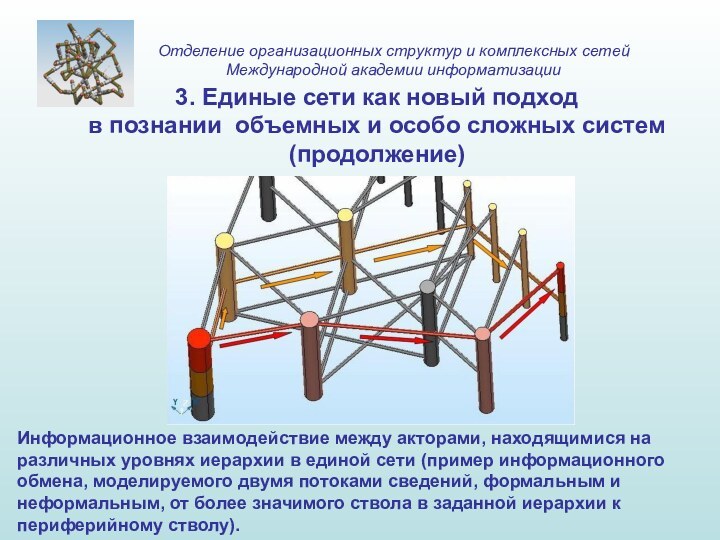
Информационное взаимодействие между акторами, находящимися на различных уровнях
иерархии в единой сети (пример информационного обмена, моделируемого двумя
потоками сведений, формальным и неформальным, от более значимого ствола в заданной иерархии к периферийному стволу).
3. Единые сети как новый подход в познании объемных и особо сложных систем (продолжение)
Слайд 25
Концепция кружева единых сетей и его структура в

слоистом представлении дают возможность изучать более глубокие отношения в
сложных системах, в сравнении с теми, что исследуются с помощью комплексных сетей. Для настоящего подхода доступными оказывается не просто широкий спектр тематических сетей, но и в их динамических взаимосвязи и взаимодействии – факторами, определяющими многие непонятные до настоящего времени процессы и явления, неоткрытые законы, которыми они регулируются.
Индивиды, организации, территориальные сообщества , государства и межгосударственные объединения являются одновременно акторами многих ТС. В целом, кружево единых сетей представляется не просто как новая научная модель, но в перспективе –оснащенный дополнительными средствами - эффективный инструмент, позволяющий находить оптимальное решение сложных задач управления, безопасного и устойчивого развития социально-экономических и биосоциальных систем международного , национального, регионального и местного масштабов.
Выводы
Слайд 26
В заключение авторы лекции выражают благодарность и искреннее

уважение к сетевым сообществам-структурам, с которыми посчастливилось эффективно и
плодотворно взаимодействовать: Международному Интернет-Проекту «Supercourse» в области эпидемиологии ( руководитель- проф. Р.Лапорт, Питтсбург, Пенсильвания, США, отв. по странам бывшего СССР – д-р Е.Шубников, Новосибирск,РФ ), Международной академии информатизации ( президент- проф. А.Харитон, Москва,РФ), Международному Союзу экономистов- Генеральному Консультанту Экономического и Социального Совета ООН ( президент – проф.Г.Попов, Москва,РФ ), Всемирной ассоциации неотложной помощи и медицины катастроф WADEM ( президент – д-р Д.Пиррос, Афины, Греция ), Фонду Эдуарда Рейна ( председатель – проф. Р.Гартц, Майен, Германия ), Европейской правовой образовательной сети LEFIS ( координатор – проф. Ф.Галиндо, Сарагоса, Испания), и многим другим организациям и лицам, также оказавшим стимулирующее и благотворное воздействие на создание новой философии кружева единых сетей .
Заключение
Слайд 27
1. URL:http://en.wiktionary.org/wiki/network (дата обращения: 04.03.2011).
2. Капица С.П. Масштаб

и смысл кризиса, его влияние на процессы модернизации// Научные
Труды Вольного экономического общества России.- 2010. Т.140.-С.116-123.
3. Эйлер Л.. Письма Эйлера Т1: На различные темы натуральной философии, адресованные германской принцессе. – Изд-во Киссиджер ЛЛС, 2007.-388 с.
4. Кениг Д. Теория конечных и бесконечных графов. –Биркаузер Бостон,1990. -426 с.
5. Галиндо Ф., Карузо А., Россодивита А.,.Тихомиров А.А, Труфанов А.И., Шубников Е.В. Перестройка топологии комплексных сетей как стратегия защиты от комбинированных атак// Энергосбережение и повышение энергетической эффективности: проблемы и решения.-М.: Инфориздат, 2010. - С. 102-106.
6. МакКарти К. ООН подрывает Форум управления Интернет. Уж эта глобальная бюрократия! Размещено 2011, 25 февраля- URL: http://www.theregister.co.uk/2011/02/25/united_nations_undermines_internet_governance_forum/(дата обращения: 04.03.2011).
7. http://www.visualcomplexity.com/vc/ (дата обращения: 04.04.2011)
8. Галиндо Ф., Дмитриенко Н.В., Карузо А., Россодивита А., Тихомиров А.А., Труфанов А.И., Шубников Е.В. Моделирование сложных атак на комплексные сети// Безопасность информационных технологий. - 2010 .№3. -C.115-121 . -URL: http://www.pvti.ru/data/file/bit/bit_3_2010_23.pdf (дата обращения: 04.03.2011).
Список основных источников