Слайд 2
Раздел 6. Демпфирование
ДЕМПФИРОВАНИЕ…………………………………………………………………………… 6 - 3
КОНСТРУКЦИОННОЕ И
ВЯЗКОЕ ДЕМПФИРОВАНИЕ………………………………… 6 - 4
КОНСТРУКЦИОННОЕ И ВЯЗКОЕ ДЕМПФИРОВАНИЕ
(ПОСТОЯННЫЕ ПЕРЕМЕЩЕНИЯ)..………………………………………………. 6 - 7
ДЕМПФИРОВАНИЕ (ВЫВОДЫ)..………………………………………………………….. 6 - 8
КОНСТРУКЦИОННОЕ ДЕМПФИРОВАНИЕ.……………………………………………… 6 - 9
ВЯЗКОЕ ДЕМПФИРОВАНИЕ.……………………………………………………………… 6 - 10
МОДАЛЬНОЕ ДЕМПФИРОВАНИЕ………………………………………………………… 6 - 18
ДЕМПФИРОВАНИЕ РЭЛЕЯ.……………………………………………………………….. 6 - 19
Слайд 3
Демпфирование
Демпфирование – это рассеивание энергии, наблюдающееся в конструкциях.
Точное
моделирование демпфирования затруднено вследствие множественности механизмов его возникновения:
Вязкостные эффекты
(буфер, амортизатор)
Внешнее трение (трение в соединениях конструкции)
Внутреннее трение (характерная особенность материала)
Структурные нелинейности (пластичность)
Аналитические зависимости, использующиеся для моделирования демпфирования
Вязкая демпфирующая сила
Конструкционная демпфирующая сила
Слайд 4
Конструкционное и вязкое демпфирование
Предположим, что колебания синусоидальные:
Тогда:
Вязкое демпфирование:
Конструкционное
демпфирование:
Слайд 5
Конструкционное и вязкое демпфирование
Уравнения идентичны, если:
Следовательно, если конструкционное
демпфирование (g) моделируется эквивалентным вязким демпфированием (b), то указанное
уравнение справедливо только на одной частоте w3 (или w4).
если
но
Слайд 6
Конструкционное и вязкое демпфирование
тогда
ζ - коэффициент апериодичности (доля
критического
демпфирования)
g = -
коэффициент конструкционного демпфирования
Q – добротность (или динамический фактор)
Слайд 7
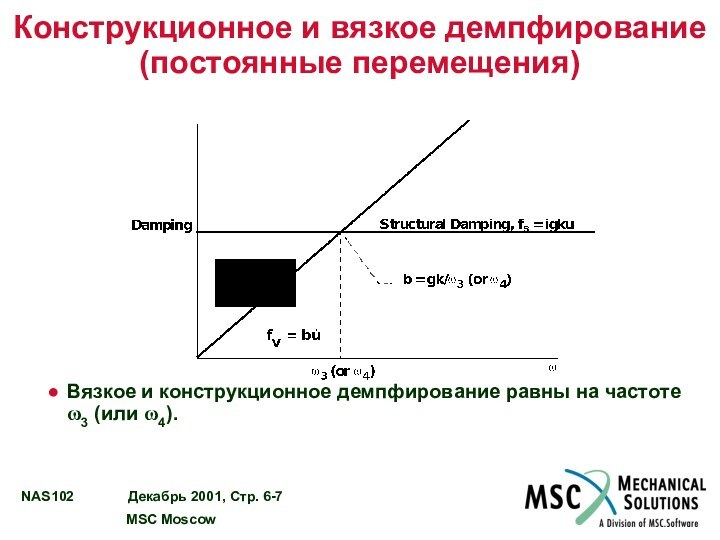
Конструкционное и вязкое демпфирование
(постоянные перемещения)
Вязкое и конструкционное
демпфирование равны на частоте ω3
(или ω4).
Слайд 8
Демпфирование (выводы)
Вязкая демпфирующая сила пропорциональна скорости
Конструкционная демпфирующая сила
пропорциональна перемещению (деформации)
Коэффициент апериодичности
Коэффициент добротности Q обратно
пропорционален величине энергии, рассеивающейся за один цикл колебаний
При резонансе
ζ = g/2
Q = 1/(2ζ)
Q = 1/g
Слайд 9
Конструкционное демпфирование
Конструкционное демпфирование
Операторы MATi
PARAM,G, (по умолчанию =
0)
Коэффициент глобального конструкционного демпфирования (умножается на глобальную матрицу жесткости
системы)
PARAM,W3, <коэффициент> (по умолчанию = 0)
Конвертирует глобальное конструкционное демпфирование в эквивалентное вязкое демпфирование
PARAM,W4, <коэффициент> (по умолчанию = 0)
Конвертирует конструкционное демпфирование в элементе в эквивалентное вязкое демпфирование
Единицы измерения W3 и W4 – рад/ед. времени
Если используется PARAM,G, <…>, то <коэффициент> в операторе PARAM,W3, … д.б. больше нуля, иначе оператор PARAM,G при анализе переходного процесса будет игнорирован (подробнее см. Раздел 7).
Слайд 10
Вязкое демпфирование
Скалярное вязкое демпфирование
Слайд 18
Модальное демпфирование
CASE CONTROL
SDAMP = n $ “инициализирует”
таблицу модального
демпфирования.
BULK DATA
TABDMP1,n,CRIT
,x1,y1,x2,y2,..endt
$ Зависимость демпфирования ("G", "CRIT" или "Q")
$ от частоты.
Слайд 19
Демпфирование Рэлея
Пропорционально матрице массе и/или матрице жесткости
Известно также
как “пропорциональное” демпфирование
Пропорциональность матрице масс PARAM,ALPHA1,
Пропорциональность матрице жесткости PARAM,ALPHA2,
Применимо
при анализе переходного процесса и анализе частотного отклика
Коэффициенты умножаются на матрицы, соответствующие наборам степеней свободы d-set (при прямом анализе) или h-set (при модальном анализе)
“Добавка” к матрице вязкого демпфирования:
[B’] = [B] + {alpha1 * [M] + alpha2 * [K]}