Слайд 2
Раздел 13. Анализ отклика на ударное широкополосное воздействие
СПЕКТР
ОТКЛИКА…….……………………………………………….. 13 - 3
ГЕНЕРИРОВАНИЕ СПЕКТРА ОТКЛИКА.………………………….. 13 - 10
ПРИМЕНЕНИЕ
СПЕКТРА....…………………………………………... 13 - 12
ПРИМЕР №9 (ЧАСТЬ I) – ГЕНЕРИРОВАНИЕ ИСХОДНОГО
УДАРНОГО СПЕКТРА………………………………………………… 13 - 21
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №9 (ЧАСТЬ I)….………… 13 - 22
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №9 (ЧАСТЬ I)….….…. 13 - 24
ПРИМЕР №9 (ЧАСТЬ II) – ПРИМЕНЕНИЕ УДАРНОГО
СПЕКТРА……………………...……………………………………….... 13 - 28
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №9 (ЧАСТЬ II)…..…….… 13 - 29
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №9 (ЧАСТЬ II)...…….. 13 - 32
Слайд 3
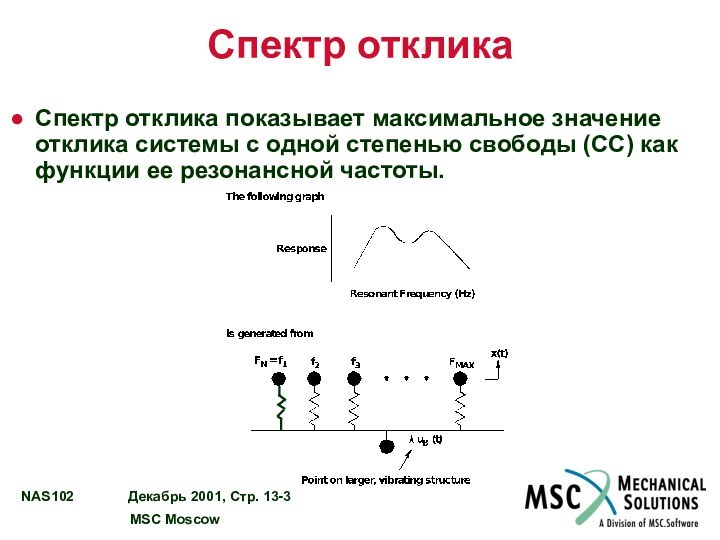
Спектр отклика
Спектр отклика показывает максимальное значение отклика системы
с одной степенью свободы (СС) как функции ее резонансной
частоты.
Слайд 4
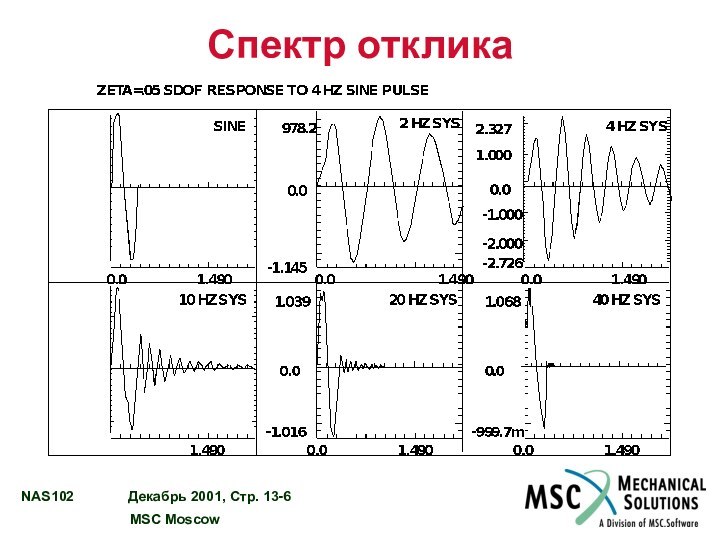
Спектр отклика
Максимум отклика каждой системы с одной СС
вычисляется по соответствующей зависимости X(t). “Базовое” перемещение UB вычисляется
по силе, прикладываемой к ней, или является вынужденным ее перемещением.
Пример. Перемещение почвы при землетрясении прикладывается к электростанции. Вычисляется спектр отклика на полу и используется для разработки оборудования (машин, трубопроводов).
Неявно предполагается, что массы осцилляторов пренебрежимо малы по сравнению с большой колеблющейся массой, что исключает действие первых на вторую. Следовательно, анализ на спектральное воздействие не связан с анализом переходного процесса.
Слайд 5
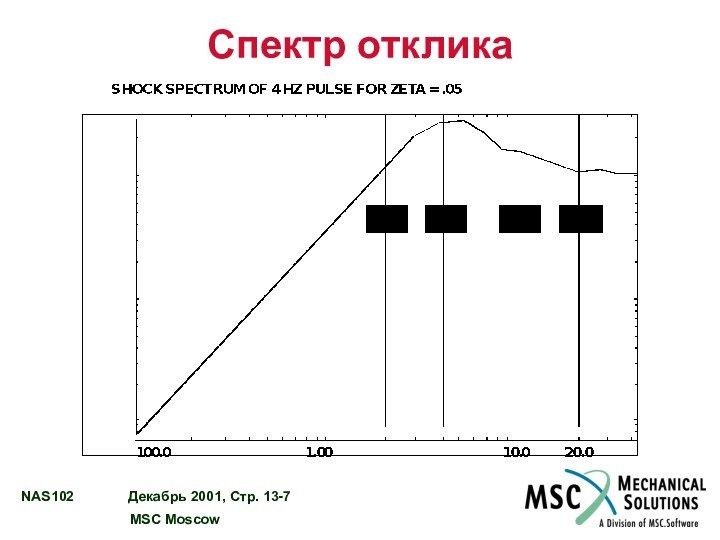
Спектр отклика
Анализ выполняется для различных величин демпфирования с
целью получения “семейства” зависимостей.
Демпфирование действует на осцилляторы, а не
на основание.
Максимальное значение отклика X(t) вычисляется для каждого осциллятора. Также вычисляется максимальное относительное перемещение каждого осциллятора и основания.
Относительные скорости и абсолютные ускорения вычисляются по относительным перемещениям
Полезные результаты - Xr, Xr, and X. Спектр, использующийся при расчетах, обычно представляется в этих величинах.
.
.
..
.
..
Слайд 8
Спектр отклика
При очень низких частотах осциллятора
При очень высоких
частотах осциллятора
Приблизительные соотношения между Xr, Xr, and X
не справедливы на очень высоких и очень низких частотах и при большом демпфировании.
Заметим, что вычисляются только амплитуды отклика, но не фазовые характеристики.
.
..
Слайд 9
Спектр отклика
Спектр отклика может вычисляться при любом типе
анализа переходного процесса (например, SOL 109, SOL 112).
Результаты анализа
переходного процесса для выбранной СС используются в качестве исходных данных для вычисления спектра отклика.
Дополнительную информацию можно найти в MSC.Nastran Advanced Dynamics User’s Guide.
Слайд 10
Генерирование спектра отклика
Необходимые операторы
Executive Control Section
SOL – необходимый
для анализа переходного процесса (например, SOL 109)
Case Control Section
XYPLOT
SPECTRAL Вычисление значений спектра
XYPUNCH SPECTRAL Печать значений спектра
Пример:
XYPUNCH ACCELERATION SPECTRAL 1/1(T1RM)
Оператор XYPLOT вычисляет набор абсолютных величин (RM) спектра ускорений по значениям записи №1 в операторе DTI,SPSEL с использованием перемещений узла №1 в X направлении (T1).
Слайд 11
Генерирование спектра отклика
Bulk Data Section
PARAM,RSPECTRA,0 Инициализация вычисления спектра
DTI,SPSEL Задание частот
и значений демпфирования
осцилляторов
FREQ Используется для задания частот и значений
демпфирования (по одному оператору FREQi)
Пример:
Слайд 12
Применение спектра
Возможно с помощью SOL 103
“Анализ переходного процесса
для бедных”. Полученный “исходный” спектр используется для вычисления отклика
каждой моды исследуемой конструкции.
Отклики мод динамической системы комбинируются для получения отклика всей системы (при этом, однако, не учитываются, поскольку не известны, сдвиги по времени между откликами мод).
Предусматривается три метода комбинирования модальных откликов: ABS, SRSS, NRL.
Слайд 13
Применение спектра
Процедура
В модели анализируемой конструкции
степени свободы, соответствующие “входным точкам”, должны быть указаны в
операторе SUPORT.
С этими степенями свободы должны быть сопряжены “большие массы” (обычно в 103 - 106 раз больше, чем масса конструкции).
Определяются моды системы (частота 0 Гц должна быть включена в исследуемый диапазон). Степени свободы, указанные в операторе SUPORT, д.б. не закреплены.
Такая модель – идеализация прикрепления исследуемой конструкции с относительно малой массой к большой воздействующей структуре (основанию).
Слайд 14
Применение спектра
Моды с частотой 0 Гц (Dm) аппроксимируют
квазистатические перемещения исследуемой конструкции.
“Фактор участия” (Participation Factors - PF)
вычисляется как
ψ = φTMDm
где φ – матрица “упругих” собственных векторов
PF используется совместно со спектром при вычислении отклика каждой моды исследуемой конструкции.
Вычисление результатов (перемещений, напряжений, сил и т.д.) производится для каждой моды на основе максимума ее отклика.
Затем эти величины комбинируются в соответствие с выбранным методом (ABS, SRSS, NRL) и выводятся.
Слайд 15
Применение спектра
Xr, отклик осциллятора с одной степенью свободы,
вычисляется в результате решения уравнения
Переходной процесс м.б. определён по
формуле
Метод ABSOLUTE
где
i – номер моды
r – индекс направления
Слайд 16
Применение спектра
Метод SRSS
где осредненное значение максимума модальной
амплитуды
равно
Метод NRL
где
- максимальное значение модальной
амплитуды
Слайд 17
Применение спектра
Необходимые операторы
Executive Control Section
SOL 103
Case Control Section
SDAMP Инициирование
оператора TABDMP1
DLOAD Задание входного спектра
METHOD Задание метода решения собственной задачи
Пример
METHOD =
1 Инициирование оператора EIRD(L),1,… в Bulk Data Section
(диапазон должен включать 0 Гц)
SDAMP = 1 Инициирование оператора TABDMP1,1,… (модальное
демпфирование)
DLOAD = 1 Инициирование оператора DLOAD,1,… в Bulk Data Section,
задающего приложение спектра к степеням свободы,
указанным в операторе SUPORT
Слайд 18
Применение спектра
Bulk Data
PARAM,SCRSPEC,0 Инициализация расчета спектрального отклика
DLOAD Задание спектра и
СС, к которым приложено воздействие
DTI,SPECSEL Задание спектра, подтверждение
соответствующего демпфирования
TABLED1 Задание амплитуды спектра
SUPORT Задание мест приложения спектрального воздействия
TABDMP1 Задание модального демпфирования в конструкции
PARAM,OPTION Задание метода комбинирования модальных результатов
Слайд 19
Применение спектра
Пример входного файла
Слайд 21
Пример №9 (Часть I)
Генерирование исходного ударного спектра
Сгенерируйте исходный
ударный спектр для исследования нагружения пластины под действием синусоидального
импульса в 2,0 дюйм/с2, прикладываемого к ее защемленному ребру. Расчетные значения демпфирования: 0, 0,02 и 0,04 от критического.
Слайд 22
Входной файл для Примера №9 (Часть I)
ID SEMINAR,

PROB9a
SOL 109
TIME 30
CEND
TITLE= TRANSIENT RESPONSE
SUBTITLE= USING DIRECT TRANSIENT METHOD
LABEL= SHOCK SPECTRUM CALCULATION
ECHO= UNSORTED
SPC= 100
SET 111= 3000
DISPLACEMENT (SORT2)= 111 $ AT LEAST DISP AND VEL MUST APPEAR
VELOCITY (SORT2)= 111
ACCELERATION ()= 111
DLOAD= 500
TSTEP= 100
$
OUTPUT (XYPLOT)
$
$ SHOCK RESPONSE IS ONLY AVAILABLE IN PLOT OR PUNCH OUTPUT. THEREFORE,
$ THE ‘OUTPUT(XYPLOT)’ SECTION OF THE CASE CONTROL MUST BE USED.
$
XGRID=YES
YGRID=YES
XYPLOT ACCE / 3000(T1)
XLOG= YES
YLOG= YES
$
$ RELATIVE SHOCK RESPONSES ARE CONTAINED IN
$IMAGINARY/PHASE
$ COMPONENTS OF THE OUTPUT
$ ABSOLUTE SHOCK RESPONSES ARE CONTAINED IN THE REAL/MAGNITUDE
$ COMPONENTS OF THE OUTPUT
$
XTITLE= FREQUENCY (CYCLES/SEC)
YTITLE= RELATIVE DISPLACEMENT
XYPLOT DISP SPECTRAL 1 / 3000 (T1IP)
YTITLE= RELATIVE VELOCITY
XYPLOT VELOCITY SPECTRAL 1 / 3000 (T1IP)
YTITLE= ABSOLUTE ACCELERATION
XYPLOT ACCELERATION SPECTRAL 1 / 3000 (T1RM)
$
$ PUNCH SHOCK SPECTRUM FOR LATER USE
$
XYPUNCH ACCELERATION SPECTRAL 1 / 3000(T1RM)
$
BEGIN BULK
$
$ DEFINE GRID POINT
$
GRID, 3000, ,0.,0.,0., ,23456
Слайд 23
Входной файл для Примера №9 (Часть I)
$
$ DEFINE
MASS
$
CMASS2, 100, 1.0, 3000, 1
$
$ APPLY LOADING TO
MASS
$
TLOAD2, 500, 600, , 0, 0., 0.004, 250., -90.
$
DAREA, 600, 3000, 1, 1.
$
$ SPECIFY INTEGRATION TIME STEPS
$
TSTEP, 100, 100, 4.0E-4, 1
$
$ PARAMETER TO CALCULATE SHOCK SPECTRUM
$
PARAM, RSPECTRA, 0
$
$ SPECIFY FREQUENCY AND DAMPING VALUES FOR
$ THE SDOF OSCILLATORS AT GRID 3000
$
DTI, SPSEL, 0
DTI, SPSEL, 1, 111, 222, 3000
$ 1= SUBCASE... 111= DAMPING... 222= FREQUENCIES... 3000= GRID NUMBER
$
$ DAMPING INFORMATION FOR OSCILLATORS
$
FREQ, 111, 0., 0.02, 0.04
$
$ NATURAL FREQUENCIES OF OSCILLATORS
$
FREQ1, 222, 20., 20., 49
$
ENDDATA
Слайд 24
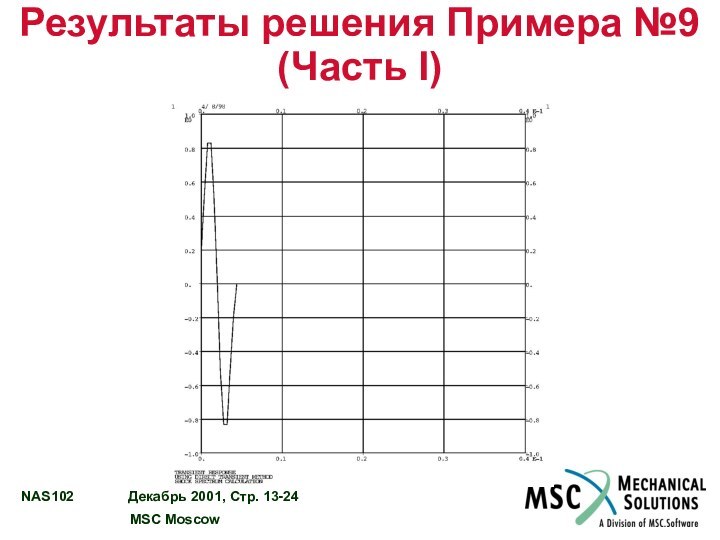
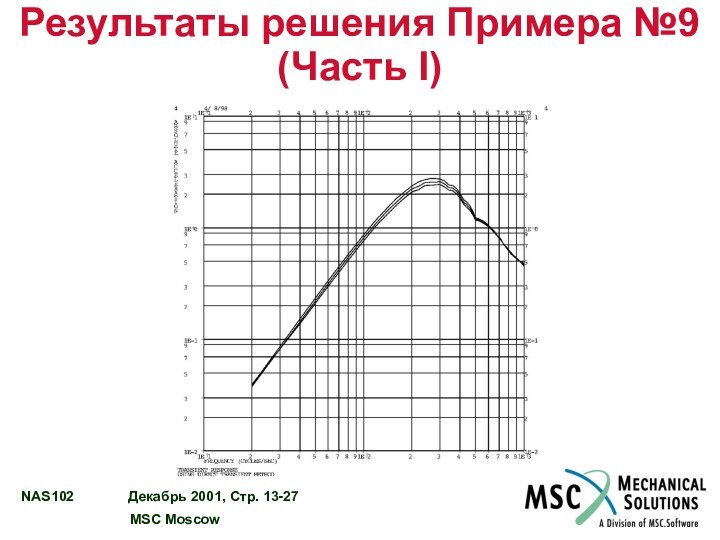
Результаты решения Примера №9 (Часть I)
Слайд 25
Результаты решения Примера №9 (Часть I)
Слайд 26
Результаты решения Примера №9 (Часть I)
Слайд 27
Результаты решения Примера №9 (Часть I)
Слайд 28
Пример №9 (Часть II)
Применение ударного спектра
Примените ударный спектр,
вычисленный в Части I, и просуммируйте отклики, используя метод
SRSS. Используйте моды конструкции с частотой до 1000 Гц и демпфирование 0,03 от критического.
Слайд 29
Входной файл для Примера №9 (Часть II)
ID SEMINAR,

PROB9b
SOL 103
TIME 30
CEND
TITLE= RESPONSE SPECTRUM ANALYSIS
SUBTITLE= USING CALCULATED SHOCK
RESPONSE
LABEL= SHOCK WILL BE INPUT IN Z DIRECTION
ECHO= UNSORTED
SET 111= ALL
DISPLACEMENT= 111
SPC= 200
SUBCASE 1
METHOD= 100
SDAMP= 200
DLOAD= 500
$
BEGIN BULK
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE
$
INCLUDE ’plate.bdf’
PARAM,COUPMASS,1
PARAM,WTMASS,0.00259
$
$ BOUNDRY CONDITIONS FOR ‘CLAMPED’ MODES
$
SPC1, 200, 1245, 1, 12, 23, 34, 45
$
$
$ PLACE BIG FOUNDATION MASS (BFM) AT BASE
$ TO STIMULATE ‘CLAMPED’ MODES
$
CMASS2, 110, 1000., 23, 3
$
$ RBE MASS TO REMAINING BASE POINTS
$
RBE2, 101, 23, 3, 1, 12, 34, 45
$
$ SUPORT CARD TO IDENTIFY EXCITATION DOFS
$
SUPORT, 23, 3
$
$ EIGENVALUE EXTRACTION
$ MUST BE MASS NORMALIZED (DEFAULT)
$
eigrl,100,0.,1000.
$
$ TABLE TO SPECIFY DAMPING FOR USE IN THE ANALYSIS
$
TABDMP1, 200, CRIT,
, 0., 0.03, 1000., 0.03, ENDT
$
$ SPECIFICATION OF SHOCK SPECTRUM TO BE USED
$
DLOAD, 500, 1.0, 2.0, 1
$
$ DLOAD, ID, OVERALL SCALE, SCALE FOR R-SET DOF# 1, SHOCK TABLE FOR $DOF# 1,
$ SCALE FOR R-SET DOF# 2, SHOCK TABLE FOR DOF# 2, ETC.
$
Слайд 30
Входной файл для Примера №9 (Часть II)
$
$ SELECT

SHOCK RESPONSE CALCULATION
$
PARAM, SCRSPEC, 0
$
$ SELECT SUMMATION OPTION
$
PARAM, OPTION,
SRSS
$
$ MODAL FREQUENCY RANGE CAN BE SELECTED USING
PARAM, LFREQ, 0.1
PARAM, HFREQ, 1000.
$
$ SPECIFICATION FOR SHOCK TABLES
$
DTI, SPECSEL, 0
DTI, SPECSEL, 1, , A, 2, 0., 3, 0.02,
, 4, 0.04, ENDREC
$
$ DTI, SPECSEL, SHOCK TABLE NUMBER, , [(A)CCELERATION, (V)ELOCITY, OR (D)ISP],
$ TABLED1 POINTER, DAMPING FOR TABLE, ETC.
$
$ PUNCH OUTPUT FOR SHOCK SPECTRUM CALCULATION
$
$ ACCE 4 3000 3 1
$ 0.000000E+00
$
TABLED1 2
20. .038683 40. .152539 60. .33511 80. .576059
100. .862049 120. 1.17619 140. 1.50169 160. 1.82018
180. 2.11404 200. 2.36801 220. 2.56617 240. 2.70027
260. 2.76275 280. 2.75073 300. 2.74632 320. 2.61887
340. 2.4218 360. 2.39068 380. 2.24931 400. 2.02296
420. 1.78538 440. 1.70355 460. 1.57056 480. 1.40493
500. 1.22608 520. 1.20483 540. 1.17631 560. 1.14097
580. 1.10048 600. 1.05582 620. 1.00818 640. .958761
660. .908725 680. .859158 700. .827667 720. .782127
740. .728996 760. .694088 780. .668602 800. .635044
820. .598496 840. .571831 860. .563072 880. .550499
Слайд 31
Входной файл для Примера №9 (Часть II)
900. .528854 920. .509281

940. .500534 960. .498016
980. .488793 1000. .468321 ENDT
$ACCE 4 3000
3 52
$ 2.0000000E-02
TABLED1 3
20. .037708 40. .143365 60. .314936 80. .541342
100. .80976 120. 1.10506 140. 1.40671 160. 1.69567
180. 1.98167 200. 2.22217 220. 2.35249 240. 2.53055
260. 2.56231 280. 2.55577 300. 2.58668 320. 2.45921
340. 2.29411 360. 2.25956 380. 2.12901 400. 1.92605
420. 1.68656 440. 1.61355 460. 1.4968 480. 1.35263
500. 1.19796 520. 1.17707 540. 1.14947 560. 1.11613
580. 1.07807 600. 1.03637 620. .992124 640. .946383
660. .900171 680. .854434 700. .810016 720. .767647
740. .727923 760. .691288 780. .658039 800. .628311
820. .602091 840. .579207 860. .559362 880. .542128
900. .526973 920. .51329 940. .500403 960. .487602
980. .474171 1000. .459408 ENDT
$ACCE 4 3000 3 103
$ 4.0000000E-02
TABLED1 4
20. .039336 40. .137673 60. .297382 80. .511244
100. .764891 120. 1.04406 140. 1.31588 160. 1.58461
180. 1.85678 200. 2.10175 220. 2.19165 240. 2.3921
260. 2.39929 280. 2.42782 300. 2.44263 320. 2.317
340. 2.17923 360. 2.14283 380. 2.0227 400. 1.8407
420. 1.62279 440. 1.53417 460. 1.43168 480. 1.30597
500. 1.17212 520. 1.15165 540. 1.12513 560. 1.09349
580. 1.05768 600. 1.01868 620. .977462 640. .934986
660. .892143 680. .849752 700. .808538 720. .769114
740. .731968 760. .69746 780. .665814 800. .637115
820. .611319 840. .588261 860. .567655 880. .549125
900. .532205 920. .516369 940. .501047 960. .485644
980. .469568 1000. .452243 ENDT
$
ENDDATA
Слайд 32
Результаты решения Примера №9 (Часть II)
1 RESPONSE

SPECTRUM ANALYSIS
APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 11
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 .0 .0 .0 1.000000E+00 .0
2 2 7.058213E+05 8.401317E+02 1.337111E+02 1.000000E+00 7.058213E+05
3 3 1.878432E+07 4.334088E+03 6.897916E+02 1.000000E+00 1.878432E+07
4 4 2.811620E+07 5.302471E+03 8.439145E+02 1.000000E+00 2.811620E+07
1 RESPONSE SPECTRUM ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 12
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
^^^ USER INFORMATION MESSAGE 9047 (POSTREIG) - SCALED RESPONSE SPECTRA FOR RESIDUAL STRUCTURE ONLY
1 RESPONSE SPECTRUM ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 13
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
0 MATRIX FN (GINO NAME 101 ) IS A DB PREC 1 COLUMN X 3 ROW RECTANG MATRIX.
0COLUMN 1 ROWS 1 THRU 3 --------------------------------------------------
ROW
1) 1.337111500777D+02 6.897918198043D+02 8.439147827213D+02
0THE NUMBER OF NON-ZERO TERMS IN THE DENSEST COLUMN = 3
0THE DENSITY OF THIS MATRIX IS 100.00 PERCENT.
1 RESPONSE SPECTRUM ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 14
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
0 PSIT
POINT VALUE POINT VALUE POINT VALUE POINT VALUE POINT VALUE
COLUMN 1
23 T3 2.11560E-02
COLUMN 2
23 T3 -5.76242E-13
COLUMN 3
23 T3 -1.18599E-02
1 RESPONSE SPECTRUM ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 15
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
U S E T D E F I N I T I O N T A B L E ( I N T E R N A L S E Q U E N C E , R O W S O R T )
R DISPLACEMENT SET
0 -1- -2- -3- -4- -5- -6- -7- -8- -9- -10-
1= 23-3
0 SCALED SPECTRAL RESPONSE, SRSS OPTION, DLOAD = 500 CLOSE = 1.00
Слайд 33
Результаты решения Примера №9 (Часть II)
PARTIAL OUTPUT FILE

FOR PROBLEM #9 (PART II) (Cont.)
1 RESPONSE SPECTRUM
ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 16
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
0 MATRIX UHVR (GINO NAME 101 ) IS A REAL 3 COLUMN X 3 ROW SQUARE MATRIX.
0COLUMN 1 ROWS 1 THRU 3 --------------------------------------------------
ROW
1) 7.6201E-08 5.0993E-20 4.8912E-10
0COLUMN 2 ROWS 1 THRU 3 --------------------------------------------------
ROW
1) 6.4019E-05 2.2101E-16 2.5935E-06
0COLUMN 3 ROWS 1 THRU 3 --------------------------------------------------
ROW
1) 5.3784E-02 9.5787E-13 1.3752E-02
0THE NUMBER OF NON-ZERO TERMS IN THE DENSEST COLUMN = 3
0THE DENSITY OF THIS MATRIX IS 100.00 PERCENT.
1 RESPONSE SPECTRUM ANALYSIS APRIL 21, 1998 MSC.Nastran 4/20/98 PAGE 17
USING CALCULATED SHOCK RESPONSE
0 SHOCK WILL BE INPUT IN Z DIRECTION SUBCASE 1
TIME = 0.000000E+00
D I S P L A C E M E N T V E C T O R
POINT ID. TYPE T1 T2 T3 R1 R2 R3
1 G .0 .0 6.222642E-10 .0 .0 .0
2 G 4.317734E-18 5.205164E-18 7.374101E-08 8.308994E-08 3.059527E-07 .0
3 G 5.986371E-18 8.477253E-18 3.173751E-07 1.214202E-07 6.616859E-07 .0
4 G 7.092405E-18 9.187666E-18 7.194814E-07 1.167081E-07 9.376687E-07 .0
5 G 8.091780E-18 8.053120E-18 1.246589E-06 1.039592E-07 1.160147E-06 .0
6 G 9.147531E-18 4.981706E-18 1.870825E-06 8.258849E-08 1.326412E-06 .0
.
.
.
49 G 1.510937E-17 5.164691E-18 1.246589E-06 1.039592E-07 1.160147E-06 .0
50 G 1.875737E-17 2.558550E-18 1.870825E-06 8.258849E-08 1.326412E-06 .0
51 G 2.006031E-17 1.356598E-18 2.565942E-06 6.149954E-08 1.444516E-06 .0
52 G 1.921646E-17 3.710099E-18 3.308983E-06 4.203441E-08 1.519611E-06 .0
53 G 1.790307E-17 3.482891E-18 4.080410E-06 2.671514E-08 1.559985E-06 .0
54 G 1.745470E-17 1.889691E-18 4.865109E-06 1.691765E-08 1.575028E-06 .0
55 G 1.757910E-17 6.847908E-19 5.653596E-06 1.301237E-08 1.577945E-06 .0