Слайд 2
ЧТО ТАКОЕ СУПЕРЭЛЕМЕНТ?…….…………………………………………………………………………… 16 - 4
КАК СУПЕРЭЛЕМЕНТ-ПОДКОНСТРУКЦИЯ

ЗАДАЕТСЯ В MSC.Nastran?…..…………………………. 16 - 5
ПРИМЕР – ШТАМПОВАННАЯ
ДЕТАЛЬ….……………………………………………………………………. 16 - 7
ВХОДНОЙ ФАЙЛ…………………………..……..……………………………………………………………….. 16 - 9
ШТАМПОВАННАЯ ДЕТАЛЬ – СУПЕРЭЛЕМЕНТ 1……………………….…………………………………. 16 - 18
ЭТАПЫ РЕШЕНИЯ…………...……………………………………………………………………………………. 16 - 19
ТЕОРИЯ СТАТИЧЕСКОЙ КОНДЕНСАЦИИ…………………………………………………………………… 16 - 21
ПРЕИМУЩЕСТВА МЕТОДА СУПЕРЭЛЕМЕНТОВ...….………………………………………...…………… 16 - 24
НЕДОСТАТКИ МЕТОДА СУПЕРЭЛЕМЕНТОВ……...……………………………………...…………………. 16 - 26
РЕШЕНИЕ ОБЫЧНЫМ МЕТОДОМ………..………………………………………...………………………… 16 - 27
АНАЛИЗ МЕТОДОМ СУПЕРЭЛЕМЕНТОВ...…………………………………….……………………………. 16 - 30
СУПЕРПОЗИЦИЯ ПАРЦИАЛЬНЫХ РЕШЕНИЙ.……………………………..……………………………… 16 - 37
МЕТОДЫ РЕДУЦИРОВАНИЯ СУПЕРЭЛЕМЕНТОВ ДЛЯ ДИНАМИЧЕСКОГО АНАЛИЗА………….. . 16 - 38
СТЕПЕНИ РЕДУЦИРОВАНИЯ..……………………………………………………………..……………………. 16 - 39
РЕДУЦИРОВАНИЕ ГАЙАНА (СТАТИЧЕСКОЕ)..……………………………………….……………………… 16 - 40
СРАВНЕНИЕ МЕТОДОВ РЕДУЦИРОВАНИЯ………………………………………………………...………… 16 - 41
ПРЕИМУЩЕСТВА МЕТОДОВ РЕДУЦИРОВАНИЯ.………………………………………………….………… 16 - 42
АНАЛИЗ СОБСТВЕННЫХ КОЛЕБАНИЙ С ИСПОЛЬЗОВАНИЕМ
ТОЛЬКО СТАТИЧЕСКОГО РЕДУЦИРОВАНИЯ………………………………………………….…………. 16 - 43
АНАЛИЗ СОБСТВЕННЫХ КОЛЕБАНИЙ С ИСПОЛЬЗОВАНИЕМ
ДИНАМИЧЕСКОГО РЕДУЦИРОВАНИЯ СУПЕРЭЛЕМЕНТОВ…………………………………………… 16 - 44
Раздел 16. Анализ собственных колебаний методом суперэлементов-подконструкций
Слайд 3
Анализ собственных колебаний методом суперэлементов-подконструкций
ОПЕРАТОР SENQSET…………………………………………………………..………………………………… 16
- 46
ОПЕРАТОР SPOINT……………………………………………………………………………………………….. 16 - 47
ОПЕРАТОР QSET…………………………………………………………………………………………………..
16 - 48
ОПЕРАТОР QSET1………………………………………………………………………………………………… 16 – 49
АНАЛИЗ СОБСТВЕННЫХ КОЛЕБАНИЙ С ИСПОЛЬЗОВАНИЕМ
ДИНАМИЧЕСКОГО РЕДУЦИРОВАНИЯ СУПЕРЭЛЕМЕНТОВ……..…………………………………… 16 - 50
ОПЕРАТОР BSET……………………….………….………………………………………………………………. 16 - 51
ОПЕРАТОР BSET1………………………………….……………………………………………………………… 16 - 52
ОПЕРАТОР CSET……………………………………….…………………………………………………………. 16 - 53
ОПЕРАТОР CSET1…………………………………….…………………………………………………………… 16 - 54
МЕТОД CMS С ЗАКРЕПЛЕННЫМИ ГРАНИЦАМИ.…………………………………………………………… 16 - 56
ПРИМЕР РЕШЕНИЯ.……………………………………………………………………………….……………….. 16 - 59
ВХОДНОЙ ФАЙЛ ДЛЯ АНАЛИЗА СОБСТВЕННЫХ КОЛЕБАНИЙ (SOL 103)..………….……………… 16 - 69
РЕЗУЛЬТАТЫ АНАЛИЗА УПРУГОЙ МОДЕЛИ МЕТОДОМ CMS...……………………...…………………. 16 - 70
Слайд 4
Что такое суперэлемент?
Физическое и математическое представления
Физическое - подструктура:
конечно-элементная модель части конструкции
Математическое – граничные матрицы: нагрузки, масса,
демпфирование и жесткость редуцируются со всех внутренних узлов в наружные или граничные узлы
Другие типы анализа с использованием подконструкций
Анализ с использованием циклической симметрии
Ввод матриц с помощью операторов GENEL и DMIG
Предусмотрено два способа описания суперэлементов
Суперэлементы - подконструкции (обсуждаются в данном разделе)
Суперэлемент типа Main Bulk Data (см. Приложение D)
Слайд 5
Как суперэлемент-подконструкция задается в MSC.Nastran?
Каждый суперэлемент полностью описывается
в отдельной полностью самодостаточной секции Bulk Data.
Суперэлемент этого типа
обычно именуется как часть в Bulk Data Section.
Описание каждого суперэлемента начинается с оператора
BEGIN [BULK] SUPER=m
и заканчивается оператором
BEGIN [BULK] SUPER=n
или оператором ENDATA
Основная секция Bulk Data Section включает полное описание остаточной структуры и других суперэлементов, не описанных как подконструкции. Эти суперэлементы (не подконструкции) могут описываться операторами SESET или SEELT. См. Приложение D для описания оператора SESET.
По умолчанию, если расстояния между узлами, принадлежащими разным подконструкциям, меньше определенного допуска, соответствующие подконструкции будут соединены с помощью этих узлов.
Вы можете переопределить величину допуска.
Слайд 6
Как суперэлемент-подконструкция задается в MSC.Nastran?
Допускается дублирование номеров узлов,
элементов, свойств и т.п. в различных подконструкциях.
Каждая подконструкция может
иметь свои нагрузки и свои модальные характеристики.
Обеспечивается вывод изображения всей модели на графопостроитель.
Суперэлемент может быть задан как копия (дубль) другого суперэлемента или введен извне.
Слайд 7
Пример – штампованная деталь
1
6
13
Слайд 8
Пример – штампованная деталь
Узлы 1 и 2 закреплены
Свойства
материала:
Сталь t = 0,05 дюйма
E = 29 x 106 фунт силы/кв. дюйм
ν = 0,3
ρ = 0,283 фунт массы/куб. дюйм (удельный
вес)
Приложенные нагрузки
Давление в 1 фунт силы/кв. дюйм на квадратные “области”
Нормальная сила в 2 дюйм силы к узлам 93 и 104
Противоположно направленные нормальные силы в 2 фунта силы к узлам 93 и 104
Слайд 9
Входной файл
$
$ file - fs1.dat
$
$
all 7 s.e. brought in using begin super
$ duplicate
boundary grids id
$ each s.e. contains its own property description with the same id
$ condensed subcase setup
$
$ -------------------------------------------------------$
id allsep1 dat
SOL 101
TIME 15
CEND
TITLE = S.E. SAMPLE PROBLEM 1
SUBTITLE = S.E. STATICS - RUN 1 - MULTIPLE LOADS
DISP = ALL
stress = all
oload = all
SET 999 = 0,1,2,3,4,5,6,7
SUPER = 999 $ ALL CASE CONTROL IS FOR ALL SUPERELEMENTS
PARAM,GRDPNT,1
SUBCASE 101
LABEL = PRESSURE LOAD
LOAD = 101
$
SUBCASE 201
LABEL = 2# NORMAL LOADS
LOAD = 201
$
SUBCASE 301
LABEL = OPPOSING LOADS
LOAD = 301
$
$
include ’plot.blk’
$
BEGIN BULK
$
CQUAD4 5 1 13 14 24 23
$
GRDSET 6
GRID 13 -.4 3.6 0.
GRID 14 .4 3.6 0.
GRID 23 -.4 4.4 0.
GRID 24 .4 4.4 0.
$
include ’prop1.blk’
$
begin super=1
$
include ’loadse1.blk’
include ’prop1.blk’
include ’se1.blk’
Слайд 10
Входной файл
$
begin super=2
$
include ’loadse2.blk’
include ’prop1.blk’
include ’se2.blk’
$
begin super=3
$
include ’prop1.blk’
include ’se3.blk’
$
begin super=4
$
include ’prop1.blk’
include ’se4.blk’
$
begin super=5
$
include
’prop1.blk’
include ’se5.blk’
$
begin super=6
$
include ’prop1.blk’
include ’se6.blk’
$
begin super=7
$
include ’prop1.blk’
include ’se7.blk’
$
enddata
Слайд 11
Входной файл
seplot 5
ptitle = superelement 5
find scale, origin

1, set 1
plot static deformation set 1 origin 1
label both
$
seplot 6
ptitle = superelement 6
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seplot 7
ptitle = superelement 7
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seplot 0
ptitle = superelement 0
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seupplot 0
ptitle = full structure
axes x,mz,y
find scale, origin 1, set 1
plot static deformation set 1 origin 1
$
$
$ plot.blk
$
output(plot)
$
set 1 = all
axes z,x,y
view 0.,0.,0.
seupplot 0
ptitle = full structure
find scale, origin 1, set 1
plot set 1 origin 1 label both
$
$ deform plots
$
seplot 1
ptitle = superelement 1
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seplot 2
ptitle = superelement 2
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seplot 3
ptitle = superelement 3
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
seplot 4
ptitle = superelement 4
find scale, origin 1, set 1
plot static deformation set 1 origin 1 label both
$
Слайд 12
Входной файл
GRID 33

-5.2 6. 0.
GRID 34 -4.4 6. 0.
GRID 37 -2. 6. 0.
GRID 38 -1.2 6. 0.
GRID 45 -5.2 6.8 0.
GRID 46 -4.4 6.8 0.
GRID 47 -3.6 6.8 0.
GRID 48 -2.8 6.8 0.
GRID 49 -2. 6.8 0.
GRID 50 -1.2 6.8 0.
GRID 57 -5.2 7.6 0.
GRID 58 -4.4 7.6 0.
GRID 59 -3.6 7.6 0.
GRID 60 -2.8 7.6 0.
GRID 61 -2. 7.6 0.
GRID 62 -1.2 7.6 0.
GRID 69 -5.2 8.4 0.
GRID 70 -4.4 8.4 0.
GRID 71 -3.6 8.4 0.
GRID 72 -2.8 8.4 0.
GRID 73 -2. 8.4 0.
GRID 74 -1.2 8.4 0.
GRID 81 -5.2 9.2 0.
GRID 82 -4.4 9.2 0.
GRID 83 -3.6 9.2 0.
GRID 84 -2.8 9.2 0.
GRID 85 -2. 9.2 0.
GRID 86 -1.2 9.2 0.
GRID 93 -5.2 10. 0.
GRID 94 -4.4 10. 0.
GRID 95 -3.6 10. 0.
GRID 96 -2.8 10. 0.
GRID 97 -2. 10. 0.
GRID 98 -1.2 10. 0.
$
$ se1.blk
$
CQUAD4 18 1 33 34 46 45
CQUAD4 19 1 34 35 47 46
CQUAD4 20 1 35 36 48 47
CQUAD4 21 1 36 37 49 48
CQUAD4 22 1 37 38 50 49
CQUAD4 23 1 45 46 58 57
CQUAD4 24 1 46 47 59 58
CQUAD4 25 1 47 48 60 59
CQUAD4 26 1 48 49 61 60
CQUAD4 27 1 49 50 62 61
CQUAD4 28 1 57 58 70 69
CQUAD4 29 1 58 59 71 70
CQUAD4 30 1 59 60 72 71
CQUAD4 31 1 60 61 73 72
CQUAD4 32 1 61 62 74 73
CQUAD4 33 1 69 70 82 81
CQUAD4 34 1 70 71 83 82
CQUAD4 35 1 71 72 84 83
CQUAD4 36 1 72 73 85 84
CQUAD4 37 1 73 74 86 85
CQUAD4 38 1 81 82 94 93
CQUAD4 39 1 82 83 95 94
CQUAD4 40 1 83 84 96 95
CQUAD4 41 1 84 85 97 96
CQUAD4 42 1 85 86 98 97
$
GRDSET 6
$
6
$ boundary grids
$
GRID 35 -3.6 6. 0.
GRID 36 -2.8 6. 0.
$

$ se2.blk
$
CQUAD4 43 1 39 40 52 51
CQUAD4 44 1 40 41 53 52
CQUAD4 45 1 41 42 54 53
CQUAD4 46 1 42 43 55 54
CQUAD4 47 1 43 44 56 55
CQUAD4 48 1 51 52 64 63
CQUAD4 49 1 52 53 65 64
CQUAD4 50 1 53 54 66 65
CQUAD4 51 1 54 55 67 66
CQUAD4 52 1 55 56 68 67
CQUAD4 53 1 63 64 76 75
CQUAD4 54 1 64 65 77 76
CQUAD4 55 1 65 66 78 77
CQUAD4 56 1 66 67 79 78
CQUAD4 57 1 67 68 80 79
CQUAD4 58 1 75 76 88 87
CQUAD4 59 1 76 77 89 88
CQUAD4 60 1 77 78 90 89
CQUAD4 61 1 78 79 91 90
CQUAD4 62 1 79 80 92 91
CQUAD4 63 1 87 88 100 99
CQUAD4 64 1 88 89 101 100
CQUAD4 65 1 89 90 102 101
CQUAD4 66 1 90 91 103 102
CQUAD4 67 1 91 92 104 103
$
GRDSET 6
$
$ boundary grids
$
GRID 41 2.8 6. 0.
GRID 42 3.6 6. 0.
$
$
GRID 39 1.2 6. 0.
GRID 40 2. 6. 0.
GRID 43 4.4 6. 0.
GRID 44 5.2 6. 0.
$
GRID 51 1.2 6.8 0.
GRID 52 2. 6.8 0.
GRID 53 2.8 6.8 0.
GRID 54 3.6 6.8 0.
GRID 55 4.4 6.8 0.
GRID 56 5.2 6.8 0.
GRID 63 1.2 7.6 0.
GRID 64 2. 7.6 0.
GRID 65 2.8 7.6 0.
GRID 66 3.6 7.6 0.
GRID 67 4.4 7.6 0.
GRID 68 5.2 7.6 0.
GRID 75 1.2 8.4 0.
GRID 76 2. 8.4 0.
GRID 77 2.8 8.4 0.
GRID 78 3.6 8.4 0.
GRID 79 4.4 8.4 0.
GRID 80 5.2 8.4 0.
GRID 87 1.2 9.2 0.
GRID 88 2. 9.2 0.
GRID 89 2.8 9.2 0.
GRID 90 3.6 9.2 0.
GRID 91 4.4 9.2 0.
GRID 92 5.2 9.2 0.
GRID 99 1.2 10. 0.
GRID 100 2. 10. 0.
GRID 101 2.8 10. 0.
GRID 102 3.6 10. 0.
GRID 103 4.4 10. 0.
GRID 104 5.2 10. 0.
$
Слайд 14
Входной файл
$
$ se3.blk
$
CQUAD4 14 1 19 20 30 29
CQUAD4 15 1 29 30 36 35
$
GRDSET 6
$
$ boundary grids
$
GRID 19 -3.6 4.4 0.
GRID 20 -2.8 4.4 0.
GRID 35 -3.6 6. 0.
GRID 36 -2.8 6. 0.
$
GRID 29 -3.6 5.2 0.
GRID 30 -2.8 5.2 0.
$
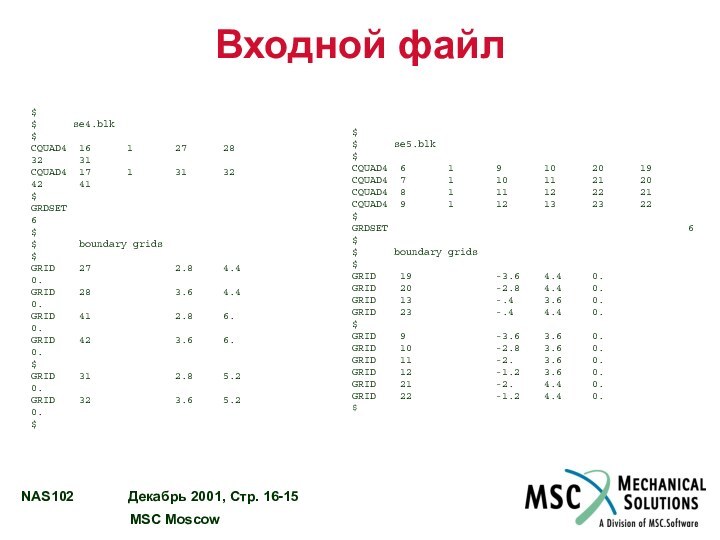
Слайд 15
Входной файл
$
$ se4.blk
$
CQUAD4 16 1 27 28 32 31
CQUAD4 17 1 31 32 42 41
$
GRDSET 6
$
$ boundary grids
$
GRID 27 2.8 4.4 0.
GRID 28 3.6 4.4 0.
GRID 41 2.8 6. 0.
GRID 42 3.6 6. 0.
$
GRID 31 2.8 5.2 0.
GRID 32 3.6 5.2 0.
$
$
$ se5.blk
$
CQUAD4 6 1 9 10 20 19
CQUAD4 7 1 10 11 21 20
CQUAD4 8 1 11 12 22 21
CQUAD4 9 1 12 13 23 22
$
GRDSET 6
$
$ boundary grids
$
GRID 19 -3.6 4.4 0.
GRID 20 -2.8 4.4 0.
GRID 13 -.4 3.6 0.
GRID 23 -.4 4.4 0.
$
GRID 9 -3.6 3.6 0.
GRID 10 -2.8 3.6 0.
GRID 11 -2. 3.6 0.
GRID 12 -1.2 3.6 0.
GRID 21 -2. 4.4 0.
GRID 22 -1.2 4.4 0.
$
$ se6.blk
$
CQUAD4 10 1 14 15 25 24
CQUAD4 11 1 15 16 26 25
CQUAD4 12 1 16 17 27 26
CQUAD4 13 1 17 18 28 27
$
GRDSET 6
$
$ boundary grids
$
GRID 27 2.8 4.4 0.
GRID 28 3.6 4.4 0.
GRID 14 .4 3.6 0.
GRID 24 .4 4.4 0.
$
GRID 15 1.2 3.6 0.
GRID 16 2. 3.6 0.
GRID 17 2.8 3.6 0.
GRID 18 3.6 3.6 0.
$
GRID 25 1.2 4.4 0.
GRID 26 2. 4.4 0.
$
$
$ se7.blk
$
CQUAD4 1 1 1 2 4 3
CQUAD4 2 1 3 4 6 5
CQUAD4 3 1 5 6 8 7
CQUAD4 4 1 7 8 14 13
$
GRDSET 6
$
GRID 1 -.4 0. 0. 123456
GRID 2 .4 0. 0. 123456
GRID 3 -.4 0.9 0.
GRID 4 .4 0.9 0.
GRID 5 -.4 1.8 0.
GRID 6 .4 1.8 0.
GRID 7 -.4 2.7 0.
GRID 8 .4 2.7 0.
$
$ boundary grids
$
GRID 13 -.4 3.6 0.
GRID 14 .4 3.6 0.
$
Слайд 17
Входной файл
$
$ prop1.blk
$
MAT1,1,30.+6,,.3,.283
PARAM,WTMASS,.00259
PARAM,AUTOSPC,YES
PSHELL,1,1,.05,1,,1
$
$
$ file - loadse1.blk
$ loads
on s.e. 1
$
$ LOAD CASE 1 - PRESSURE LOAD
$
PLOAD2,101,-1.,18,THRU,42
$
$
LOAD CASE 2 - 2 POINT LOADS AT CORNERS
$
FORCE,201,93,,2.,0.,0.,1.
$
$ LOAD CASE 3 - OPPOSING POINT LOADS AT CORNERS
$
FORCE,301,93,,2.,0.,0.,1.
$
$
$ file - loadse2.blk
$ loads on s.e. 2
$
$ LOAD CASE 1 - PRESSURE LOAD
$
PLOAD2,101,-1.,43,THRU,67
$
$ LOAD CASE 2 - 2 POINT LOADS AT CORNERS
$
FORCE,201,104,,2.,0.,0.,1.
$
$ LOAD CASE 3 - OPPOSING POINT LOADS AT CORNERS
$
FORCE,301,104,,2.,0.,0.,-1.
$
Слайд 18
Штампованная деталь – суперэлемент 1
Слайд 19
Этапы решения
Степени свободы (СС) каждого суперэлемента делятся на
два поднабора:
Внешние СС (называемые A-set): сохраняются для дальнейшей обработки
(решения) (для суперэлемента 1 - это узлы 35 и 36)
Внутренние СС: редуцируются в процессе обработки суперэлемента и не учитываются при дальнейшем решении (для суперэлемента 1 - это узлы 33, 34, 37, 38, 45-50, 57-62, 69-74, 81-86, 93-98).
Слайд 20
Этапы решения
Для каждого суперэлемента его поведение описывается матричными
уравнениями, содержащими граничные (или внешние) СС.
Для каждого суперэлемента вычисляются
матрицы размерности G-set.
Эти матрицы редуцируются в матрицы, представляющие свойства суперэлемента “с точки зрения” примыкающей части конструкции.
На уровне остаточной структуры производится “сборка” всех граничных матриц.
Bulk Data Section для остаточной структуры содержит все “остальные” данные для части, не описанной как суперэлемент, и некоторые общие данные.
Вычисляются перемещения остаточной структуры.
Для каждого суперэлемента по граничным перемещениям определяются перемещения внутренних узлов.
Слайд 21
Теория статической конденсации
После построения матриц и учета MPC
и SPC,
Kff Uf = Pf
O-Set - внутренние узлы (редуцируются)
A-Set
- внешние (или граничные) узлы (сохраняются)
Разделение СС
Слайд 22
Теория статической конденсации
Верхнее уравнение умножается слева на Koo-1
Обозначим (граничное
преобразование)
(относительное перемещение)
тогда (суммарное
внутреннее перемещение)
Слайд 23
Подставим выражение для Uo в нижнее уравнение
тогда (граничная жесткость)
и (граничные
нагрузки)
Решение для остаточной структуры
Ua = Kaa-1 Pa (граничные перемещения)
Теория статической конденсации
Слайд 24
Преимущества метода суперэлементов
Возможность решения задач, превосходящих по своим
размерам, возможности Вашей ЭВМ.
Меньшие затраты процессорного и общего времени
(меньшие потери при неудачном решении, т.к. каждый суперэлемент может обрабатываться отдельно).
Частичное изменение конструкции объекта предполагает только частичное выполнение нового решения.
Большие возможности управления ресурсами ЭВМ.
Пошаговый ввод информации
Организационные преимущества
Использование повторяемости компонентов
Пошаговый вывод информации
Организационные преимущества
Улучшение понимания
Компоненты конструкции могут моделироваться предприятиями - соисполнителями работ.
Слайд 25
Преимущества метода суперэлементов
Многошаговое редуцирование для динамического анализа
Возможность выполнения
глобально-локального анализа
Возможность проведения исследований вариантов конструкции (“Что, если...”)
Слайд 26
Недостатки метода суперэлементов
Увеличение затрат ресурсов ЭВМ в связи
с компиляцией модулей DMAP, манипуляциями с базами данных и
их увеличением
Применение статической конденсации при малой величине модели может свести “на нет” получаемую экономию.
Остаточная структура не перенумеруется и ее матрица жесткости обычно плотно заполненная.
Все суперэлементы должны быть линейными.
Для массы и демпфирования аппроксимация при динамическом анализе должна быть выполнена методом статического редуцирования, методом синтеза модальных компонент или методом обобщенного динамического редуцирования.
Автоматический рестарт возможен только в SOL 101 и последующих.
Слайд 27
Решение обычным методом
Последовательность
Слайд 28
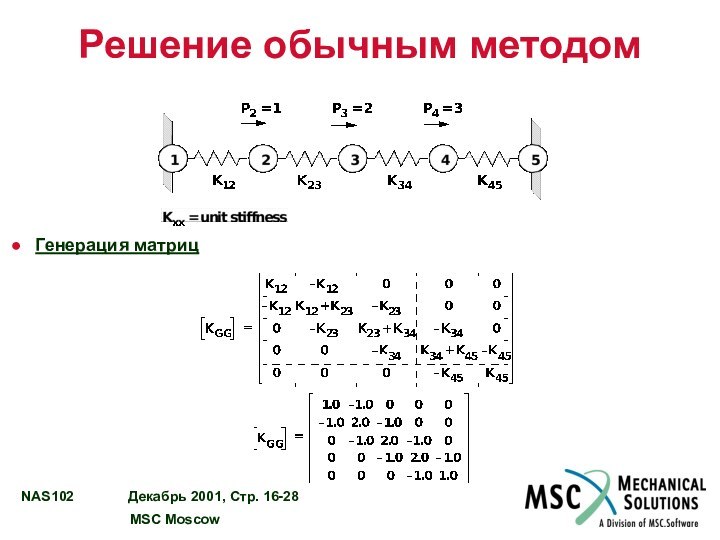
Решение обычным методом
Генерация матриц
Слайд 29
Решение обычным методом
Учет закреплений и решение
Слайд 30
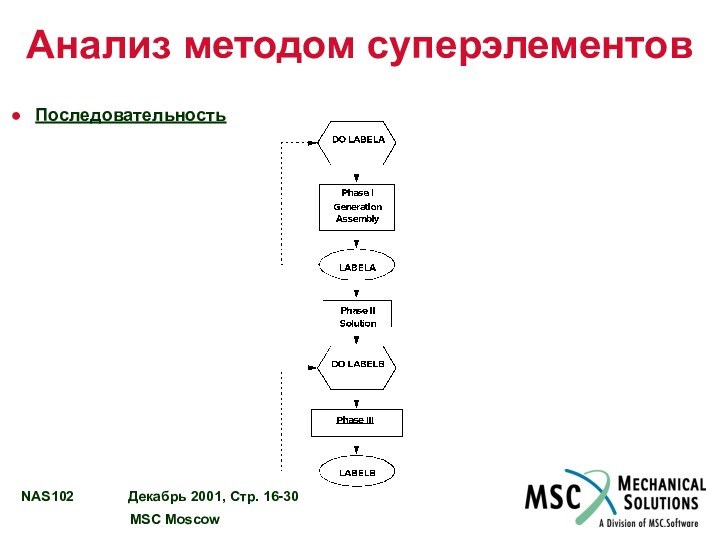
Анализ методом суперэлементов
Последовательность
Слайд 31
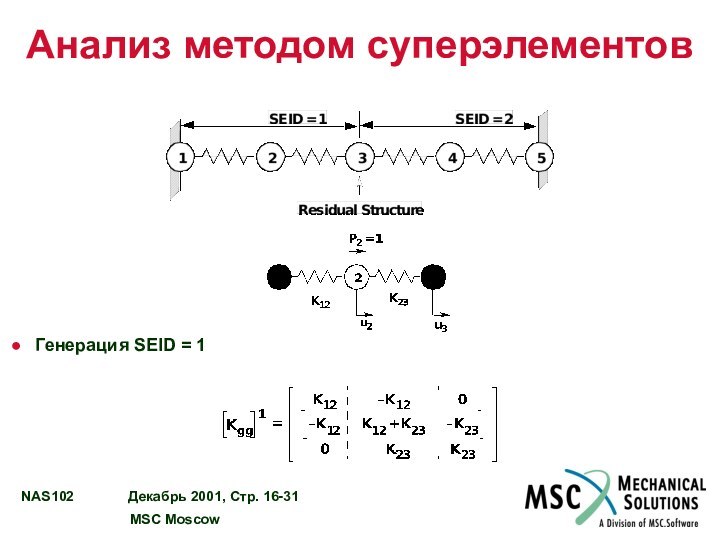
Анализ методом суперэлементов
Генерация SEID = 1
Слайд 32
Анализ методом суперэлементов
Редуцирование SEID = 1
Удаление закреплений:
Вычисление граничных
преобразований:
Слайд 33
Анализ методом суперэлементов
Вычисление граничной жесткости:
Вычисление граничных нагрузок:
Слайд 34
Анализ методом суперэлементов
Аналогично SEID = 2
Слайд 35
Анализ методом суперэлементов
Остаточная структура
“Сборка”
Решение
Слайд 36
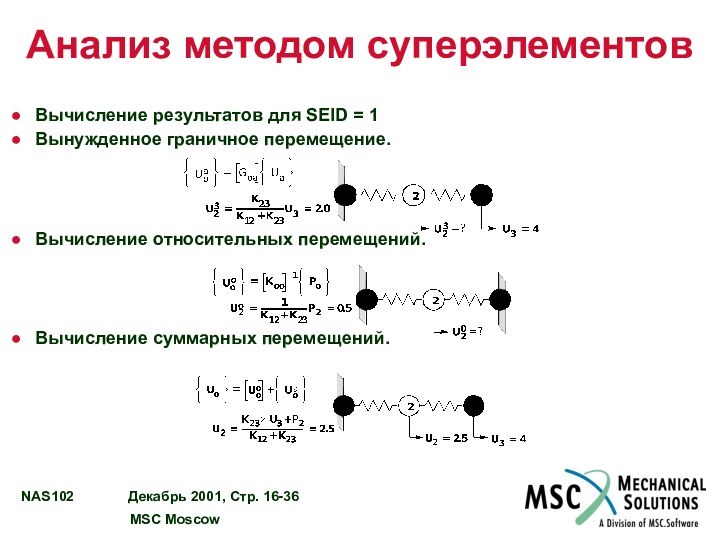
Анализ методом суперэлементов
Вычисление результатов для SEID = 1
Вынужденное
граничное перемещение.
Вычисление относительных перемещений.
Вычисление суммарных перемещений.
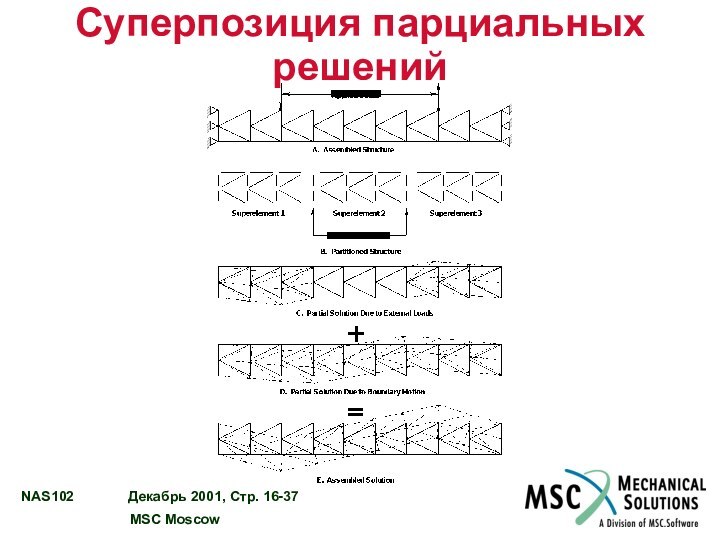
Слайд 37
Суперпозиция парциальных решений
Слайд 38
Методы редуцирования суперэлементов для динамического анализа
Статическое редуцирование
Статическое редуцирование
жесткости и редуцирование масс методом Гайана
Динамическое редуцирование
Обобщенное динамическое редуцирование
(GDR)
Синтез модальных компонент (CMS)
Аналитическое (SOL 103)
Слайд 39
Степени редуцирования
Статическое редуцирование (по умолчанию)
Внутренние массы концентрируются в
граничные узлы (редуцирование Гайана)
Свойства жестких тел сохраняются
Важные массы должны
быть объявлены внешними (граничными)
Обобщенное динамическое редуцирование – в дополнение к статическому редуцированию
Внутренние массы представляются приближенными (аппроксимирующими) собственными векторами
Приближенные собственные частоты и формы м.б. выведены в качестве промежуточных результатов
Редуцирование модальных компонент – в дополнение к статическому редуцированию
Внутренние массы представляются точными собственными векторами компонентов модели
Собственные векторы для каждого суперэлемента м.б. выведены
Слайд 40
Редуцирование Гайана (статическое)
Основывается на жесткости
Выполняется статическая конденсация жесткости
Если
Po=0, тогда {uo} = [Goa] {ua}, где Goa
= -[Koo-1] [Koa]
Это преобразование обеспечивает переход от F-set к A-set
Однако, (внутренние динамические эффекты) игнорируется
При отсутствии масс, демпфирования и нагрузок, ассоциирующихся с внутренними узлами (O-set), аппроксимация отсутствует (нет погрешности).
Если собственные частоты и частоты воздействия намного выше собственных частот остаточной структуры и частот воздействия, - точность высокая.
Слайд 41
Сравнение методов редуцирования
Статическое редуцирование
Обобщенное динамическое редуцирование
Аппроксимирующие собственные векторы
представляют внутренние перемещения.
Редуцирование модальных компонент
Точные собственные векторы представляют внутренние
перемещения.
Слайд 42
Преимущества методов редуцирования
Преимущества метода Редуцирования модальных компонент над
методом Статического редуцирования
Возможно использовать опытные результаты
Более точен при одинаковом
количестве динамических СС
Идеален для высоко связанных и несвязанных конструкций
Преимущества метода Статического редуцирования над методом Редуцирования модальных компонент
Дешевле
Менее сложный
Меньше проблем
Слайд 43
Анализ собственных колебаний с использованием только статического редуцирования
Не
требуется обобщенных переменных для суперэлементов (за исключением остаточной структуры
– если для нее требуется обобщенное редуцирование или редуцирование модальных компонент)
Масса, демпфирование и жесткость суперэлемента конденсируется статически во внешние СС.
Операторы ASETi и QSETi могут быть указаны только в остаточной структуре.
При отсутствии операторов ASETi все внутренние СС остаточной структуры сохраняются для анализа собственных колебаний.
При наличии операторов ASETi, только соответствующие СС сохраняются для анализа собственных колебаний.
Раздел Case Control Section аналогичен статическому анализу, требуется только дополнительно оператор METHOD в SUBCASE’е, относящемся к остаточной структуре. Может применяться оператор DYNRED.
Слайд 44
Анализ собственных колебаний с использованием динамического редуцирования суперэлементов
Поведение

суперэлемента описывается его реальными и/или “обобщенными” (GDR) модами в
дополнении к статическим формам.
Жесткость, масса и демпфирование суперэлемента трансформируются с использованием физических и модальных координат.
Моды суперэлемента вычисляются при наличии операторов METHOD и/или DYNRED (GDR) в соответствующем SUBCASE’е.
Количество мод суперэлемента задается операторами EIGR или EIGRL (DYNRED для обобщенного динамического редуцирования).
Количество мод суперэлемента, передаваемых в остаточную структуру, определяется операторами SENQSET или QSETi и SPOINT.
Если моды суперэлемента (СЭ) передаются для решения в другой СЭ, то надо использовать операторы QSETi и SPOINT. Операторы SPOINT должны соответствовать скалярным переменным в “нижнем” суперэлементе (соответствие определяется оператором SECONCT).
По умолчанию, моды суперэлемента вычисляются с фиксированными границами (в B-set). Этот прием известен как метод Крейга-Бамптона (Craig-Bampton).
Слайд 45
Анализ собственных колебаний с использованием динамического редуцирования суперэлементов
Моды
суперэлемента вычисляются в Фазе I в соответствие с операцией
SEMR.
Суперэлементы-копии должны иметь номера внешних узлов, аналогичные номерам граничных узлов суперэлемента-оригинала. Если СЭ-оригинал включает оператор SENQSET, тогда СЭ-копия должен иметь соответствующие СС для представления мод.
Слайд 50
Анализ собственных колебаний с использованием динамического редуцирования суперэлементов
При
вычислении мод полностью незакрепленного суперэлемента все внешние СС д.б.
перечислены в операторе CSETi.
Бездеформационные моды (f=0 Гц) – линейные комбинации статических векторов и не должны быть редуцированы.
Одно из двух:
Не вычисляйте их (F1>0 в операторах EIGR или EIGRL).
Вычисляйте и надейтесь, что программа удалит их (см. оператор PARAM,EPSRC в MSC.Nastran Reference Manual).
“Смешанные” моды могут быть вычислены с использованием операторов CSETi и BSETi для задания закрепленных и незакрепленных степеней свободы.
При наличии “смешанных” мод с частотой 0 Гц с ними нужно “обращаться” аналогично случаю полностью незакрепленного суперэлемента.
Слайд 56
Метод CMS с закрепленными границами
Описание методики (известной как
метод Крейга-Бамптона)
Степени свободы суперэлемента подразделяются на два набора (set’а).
Первый набор (B-set) относится к граничным узлам. Второй набор – это внутренние степени свободы (O-set).
Вычисляются “статические” моды, каждая из которых является перемещением суперэлемента вследствие единичного изменения одной из граничных степеней свободы (другие при этом остаются неподвижными). Т.о., количество “статических” мод равно количеству граничных СС (эти векторы в MSC.Nastran известны как GOAT)
В матричном виде
(в действительности Pb не прикладывается)
Из первого уравнения
Слайд 57
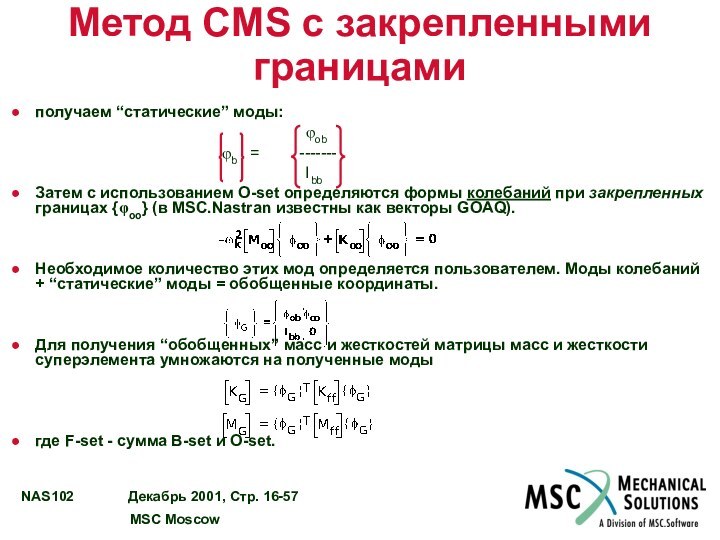
Метод CMS с закрепленными границами
получаем “статические” моды:
φob
φb = -------
Ibb
Затем с использованием O-set определяются формы колебаний при закрепленных границах {φoo} (в MSC.Nastran известны как векторы GOAQ).
Необходимое количество этих мод определяется пользователем. Моды колебаний + “статические” моды = обобщенные координаты.
Для получения “обобщенных” масс и жесткостей матрицы масс и жесткости суперэлемента умножаются на полученные моды
где F-set - сумма B-set и O-set.
Слайд 58
Метод CMS с закрепленными границами
“Обобщенные” матрицы включают физические
СС, относящиеся к граничным узлам, и модальные координаты (при
закрепленных границах суперэлемента).
Полученные матрицы могут обрабатываться как и другие структурные матрицы а результаты – вычисляться обычным методом при модальном решении (обобщенные координаты умножаются на соответствующий вектор и участвуют в формировании относительных перемещений).
Вычисляемые моды нормируются по величине (1,0) их максимальных перемещений (вне зависимости от метода нормирования, затребованного пользователем).
Слайд 59
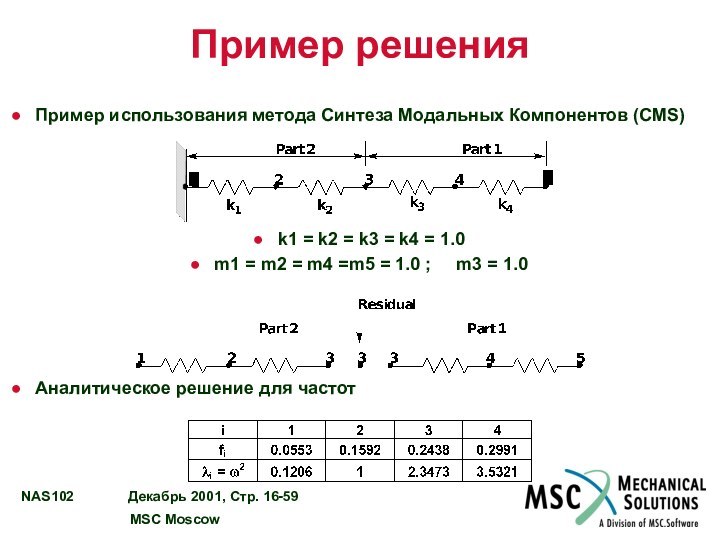
Пример решения
Пример использования метода Синтеза Модальных Компонентов (CMS)
k1
= k2 = k3 = k4 = 1.0
m1 =
m2 = m4 =m5 = 1.0 ; m3 = 1.0
Аналитическое решение для частот
Слайд 60
Пример решения
Суперэлемент 1
Узел 3 - граничный; решение для
“статических” мод:
где Koo =
Kob =
=
Koo-1
Слайд 61
Пример решения
где φob = -
1.0 1.0 -1.0
= 1.0
1.0 2.0 0.0 1.0
φb =
Моды колебаний при закрепленных границах.
Замечание: В MSC.Nastran используются моды, нормированные до
значения 1,0 их максимального перемещения.
Нормализация выполняется при решении собственной
задачи.
Слайд 62
Пример решения
где 1001 и 1002 – скалярные переменные,
используемые для представления мод суперэлемента 1.
Слайд 63
Пример решения
Суперэлемент 2
где 1005 - скалярная переменная, используемая
для представления моды суперэлемента 2.
Слайд 64
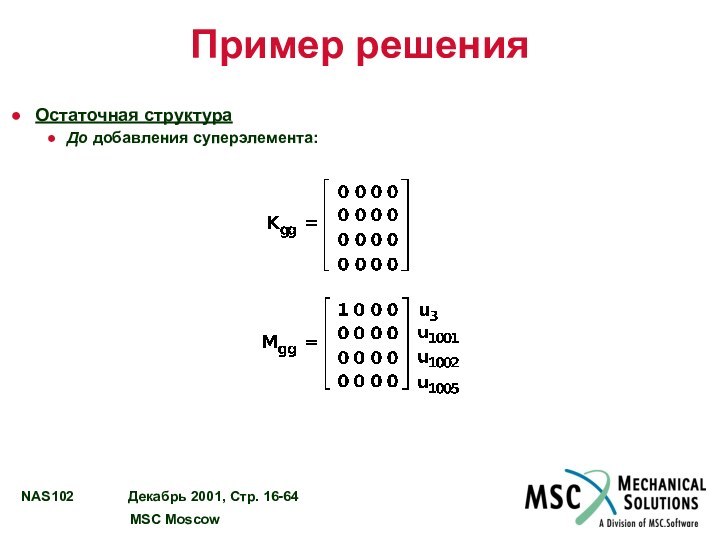
Пример решения
Остаточная структура
До добавления суперэлемента:
Слайд 65
Пример решения
Добавление суперэлемента 1
Слайд 66
Пример решения
Добавление суперэлемента 2
Слайд 67
Пример решения
Решение {KFF - ω2Mff}{φf} дает ω2 =
0.1206, 1.0000, 2.3473, 3.5321.
Вычисление результатов (перемещение узлов для моды
1)
Остаточная структура
Слайд 68
Пример решения
Суперэлемент 2
Суперэлемент 1
Слайд 69
Входной файл для анализа собственных колебаний (SOL 103)
Слайд 70
Результаты анализа упругой модели методом CMS
OUTPUT FROM SPRING
MODEL CMS RUN
1 SAMPLE PROBLEM FOR CMS USING
PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 25
SUPERELEMENT 1
0 SUBCASE 1
0
E I G E N V A L U E A N A L Y S I S S U M M A R Y (REIGL MODULE)
BLOCK SIZE USED ...................... 1
NUMBER OF DECOMPOSITIONS ............. 1
NUMBER OF ROOTS FOUND ................ 2
NUMBER OF SOLVES REQUIRED ............ 3
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 26
SUPERELEMENT 1
0 SUBCASE 1
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 3.819660E-01 6.180340E-01 9.836316E-02 1.000000E+00 3.819660E-01
2 2 2.618034E+00 1.618034E+00 2.575181E-01 1.000000E+00 2.618034E+00
Слайд 71
Результаты анализа упругой модели методом CMS
OUTPUT FROM SPRING
MODEL CMS RUN
1 SAMPLE PROBLEM FOR CMS USING
PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 38
SUPERELEMENT 2
0 SUBCASE 2
0
E I G E N V A L U E A N A L Y S I S S U M M A R Y (REIGL MODULE)
BLOCK SIZE USED ...................... 1
NUMBER OF DECOMPOSITIONS ............. 1
NUMBER OF ROOTS FOUND ................ 1
NUMBER OF SOLVES REQUIRED ............ 2
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 39
SUPERELEMENT 2
0 SUBCASE 2
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 2.000000E+00 1.414214E+00 2.250791E-01 1.000000E+00 2.000000E+00
Слайд 72
Результаты анализа упругой модели методом CMS
1 SAMPLE

PROBLEM FOR CMS USING PARTS
MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 48
SUPERELEMENT 0
0 SUBCASE 100
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 1.206148E-01 3.472964E-01 5.527393E-02 1.000000E+00 1.206148E-01
2 2 1.000000E+00 1.000000E+00 1.591549E-01 1.000000E+00 1.000000E+00
3 3 2.347296E+00 1.532089E+00 2.438395E-01 1.000000E+00 2.347296E+00
4 4 3.532089E+00 1.879385E+00 2.991135E-01 1.000000E+00 3.532089E+00
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 49
SUPERELEMENT 0
0 SUBCASE 100
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 50
SUPERELEMENT 0
0 SUBCASE 100
0***USER INFORMATION MESSAGE---DATA RECOVERY FOR SUPERELEMENT 0 IS NOW INITIATED.
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 51
SUPERELEMENT 0
0 SYSTEM MODES SUBCASE 100
EIGENVALUE = 1.206148E-01
CYCLES = 5.527393E-02 R E A L E I G E N V E C T O R N O . 1
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -4.285251E-01 .0 .0 .0 .0 .0
Слайд 73
Результаты анализа упругой модели методом CMS
1 SAMPLE

PROBLEM FOR CMS USING PARTS
MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 52
SUPERELEMENT 0
0 SYSTEM MODES SUBCASE 100
EIGENVALUE = 1.000000E+00
CYCLES = 1.591549E-01 R E A L E I G E N V E C T O R N O . 2
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -5.773503E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 53
SUPERELEMENT 0
0 SYSTEM MODES SUBCASE 100
EIGENVALUE = 2.347296E+00
CYCLES = 2.438395E-01 R E A L E I G E N V E C T O R N O . 3
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G 2.280134E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 54
SUPERELEMENT 0
0 SYSTEM MODES SUBCASE 100
EIGENVALUE = 3.532089E+00
CYCLES = 2.991135E-01 R E A L E I G E N V E C T O R N O . 4
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -6.565385E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 55
SUPERELEMENT 0
0 SUBCASE 100
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 56
SUPERELEMENT 1
0 SUBCASE 100
0***USER INFORMATION MESSAGE---DATA RECOVERY FOR SUPERELEMENT 1 IS NOW INITIATED.
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 57
SUPERELEMENT 1
0 CMS FOR PART 1 SUBCASE 1
EIGENVALUE = 1.206148E-01
CYCLES = 5.527393E-02 R E A L E I G E N V E C T O R N O . 1
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -4.285251E-01 .0 .0 .0 .0 .0
4 G -5.773503E-01 .0 .0 .0 .0 .0
5 G -6.565385E-01 .0 .0 .0 .0 .0
Слайд 74
Результаты анализа упругой модели методом CMS
OUTPUT FROM SPRING

MODEL CMS RUN (Cont.)
1 SAMPLE PROBLEM FOR CMS
USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 58
SUPERELEMENT 1
0 CMS FOR PART 1 SUBCASE 1
EIGENVALUE = 1.000000E+00
CYCLES = 1.591549E-01 R E A L E I G E N V E C T O R N O . 2
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -5.773503E-01 .0 .0 .0 .0 .0
4 G 8.187895E-16 .0 .0 .0 .0 .0
5 G 5.773503E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 59
SUPERELEMENT 1
0 CMS FOR PART 1 SUBCASE 1
EIGENVALUE = 2.347296E+00
CYCLES = 2.438395E-01 R E A L E I G E N V E C T O R N O . 3
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G 2.280134E-01 .0 .0 .0 .0 .0
4 G 5.773503E-01 .0 .0 .0 .0 .0
5 G -4.285251E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 60
SUPERELEMENT 1
0 CMS FOR PART 1 SUBCASE 1
EIGENVALUE = 3.532089E+00
CYCLES = 2.991135E-01 R E A L E I G E N V E C T O R N O . 4
POINT ID. TYPE T1 T2 T3 R1 R2 R3
3 G -6.565385E-01 .0 .0 .0 .0 .0
4 G 5.773503E-01 .0 .0 .0 .0 .0
5 G -2.280134E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 61
SUPERELEMENT 1
0 SUBCASE 100
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 62
SUPERELEMENT 2
0 SUBCASE 100
0***USER INFORMATION MESSAGE---DATA RECOVERY FOR SUPERELEMENT 2 IS NOW INITIATED.
Слайд 75
Результаты анализа упругой модели методом CMS
1 SAMPLE

PROBLEM FOR CMS USING PARTS
MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 63
SUPERELEMENT 2
0 CMS FOR PART 2 SUBCASE 2
EIGENVALUE = 1.206148E-01
CYCLES = 5.527393E-02 R E A L E I G E N V E C T O R N O . 1
POINT ID. TYPE T1 T2 T3 R1 R2 R3
1 G .0 .0 .0 .0 .0 .0
2 G -2.280134E-01 .0 .0 .0 .0 .0
3 G -4.285251E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 64
SUPERELEMENT 2
0 CMS FOR PART 2 SUBCASE 2
EIGENVALUE = 1.000000E+00
CYCLES = 1.591549E-01 R E A L E I G E N V E C T O R N O . 2
POINT ID. TYPE T1 T2 T3 R1 R2 R3
1 G .0 .0 .0 .0 .0 .0
2 G -5.773503E-01 .0 .0 .0 .0 .0
3 G -5.773503E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 65
SUPERELEMENT 2
0 CMS FOR PART 2 SUBCASE 2
EIGENVALUE = 2.347296E+00
CYCLES = 2.438395E-01 R E A L E I G E N V E C T O R N O . 3
POINT ID. TYPE T1 T2 T3 R1 R2 R3
1 G .0 .0 .0 .0 .0 .0
2 G -6.565385E-01 .0 .0 .0 .0 .0
3 G 2.280134E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 66
SUPERELEMENT 2
0 CMS FOR PART 2 SUBCASE 2
EIGENVALUE = 3.532089E+00
CYCLES = 2.991135E-01 R E A L E I G E N V E C T O R N O . 4
POINT ID. TYPE T1 T2 T3 R1 R2 R3
1 G .0 .0 .0 .0 .0 .0
2 G 4.285251E-01 .0 .0 .0 .0 .0
3 G -6.565385E-01 .0 .0 .0 .0 .0
1 SAMPLE PROBLEM FOR CMS USING PARTS MAY 12, 1998 MSC.Nastran 7/17/97 PAGE 67