Презентация на тему MSC.Nastran 102 2001 - 17

NOLIN

ВНЕШНИЕ ПЕРЕМЕННЫЕ..………………………………….………………………17 - 3
ПЕРЕДАТОЧНЫЕ ФУНКЦИИ...………………………………………..……………. 17 - 4
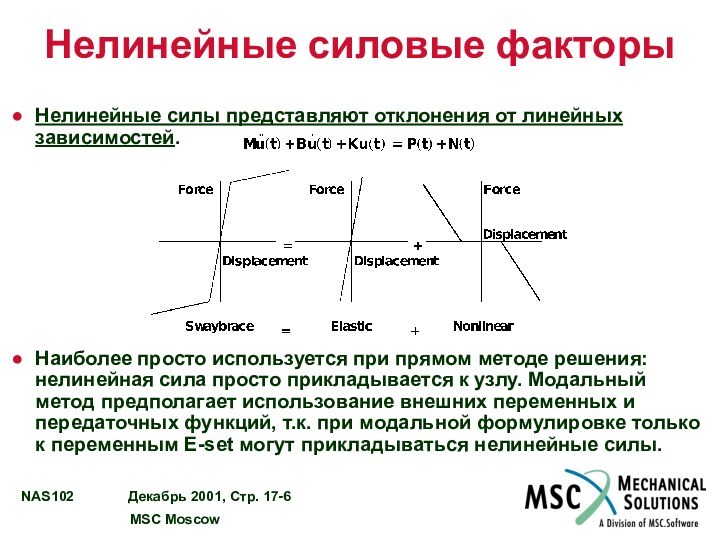
НЕЛИНЕЙНЫЕ СИЛОВЫЕ

ФАКТОРЫ.……………………………………..…… 17 - 5
ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ НЕЛИНЕЙНЫХ СИЛ………………….. 17 - 7
ЭЛЕМЕНТЫ NOLIN...………………………………………………….……………… 17 - 8
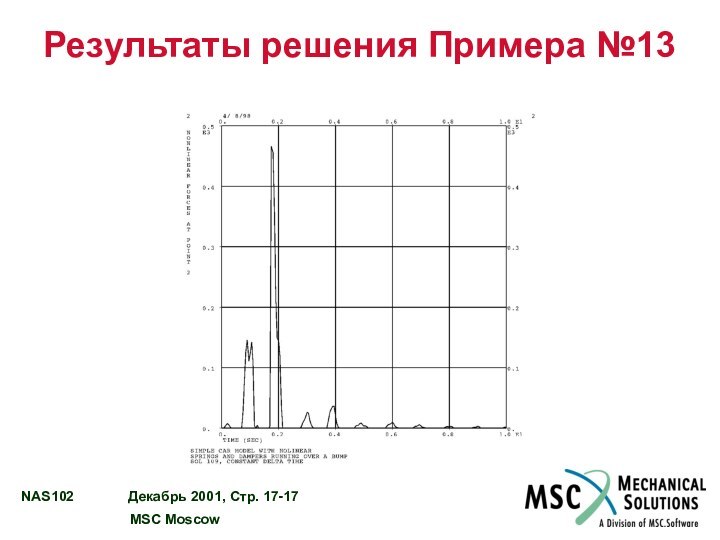
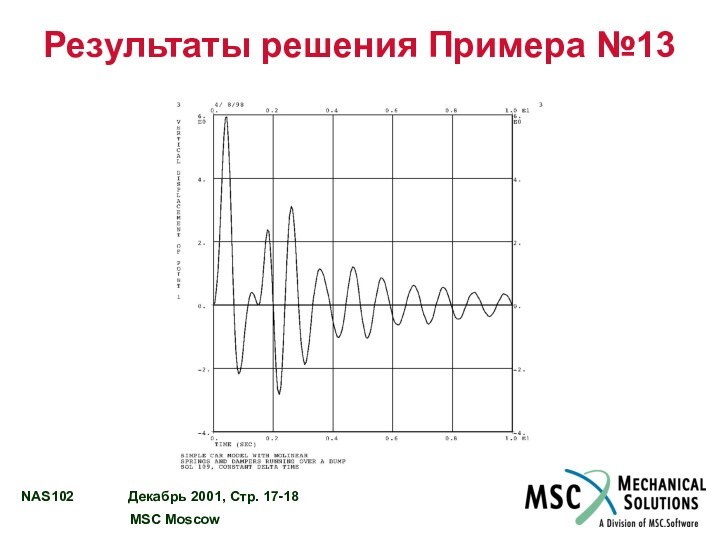
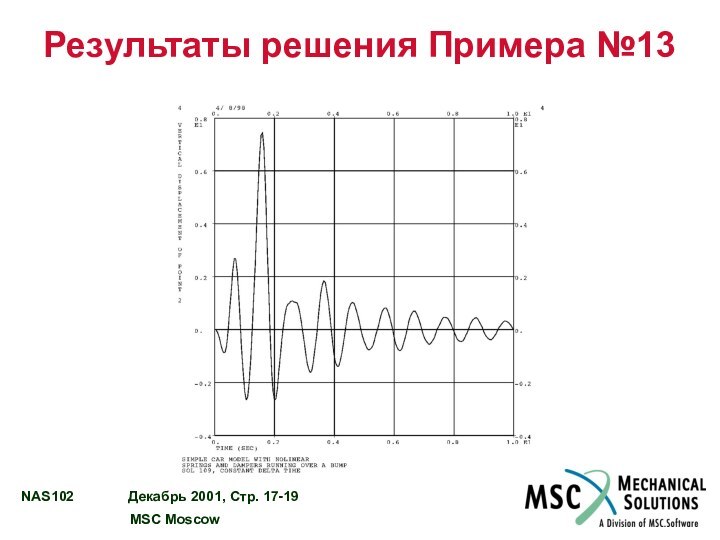
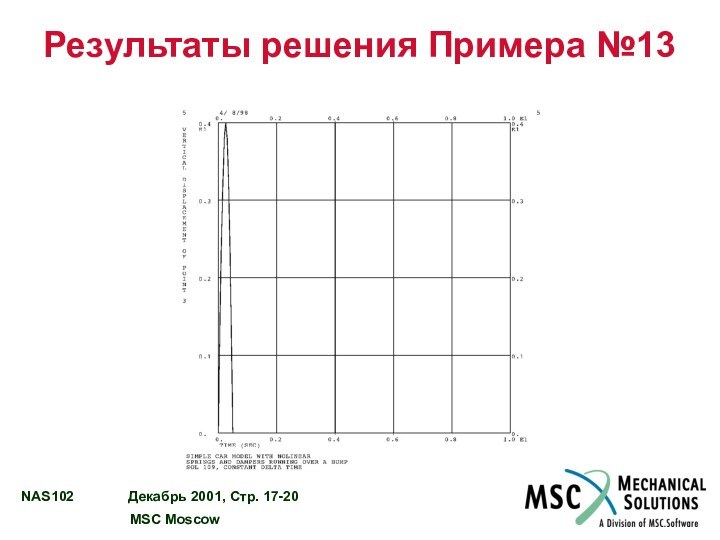
ПРИМЕР №13 – ЛИНЕЙНЫЙ АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА
С ИСПОЛЬЗОВАНИЕМ ЭЛЕМЕНТОВ NOLIN…………………………………… 17 - 10
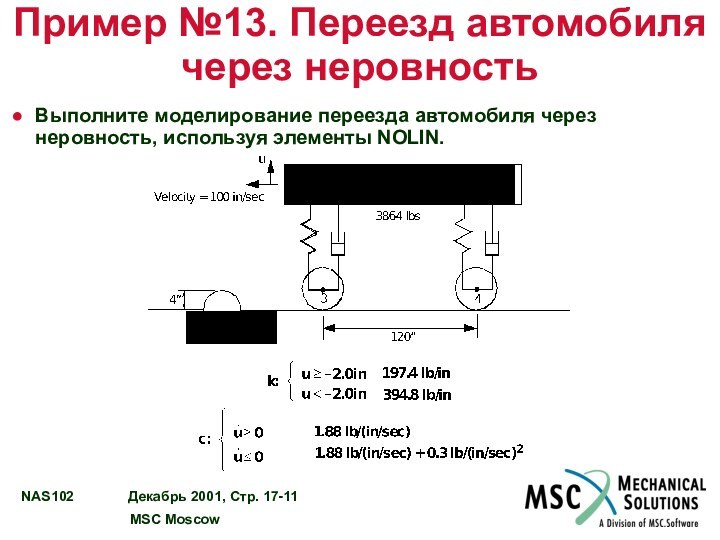
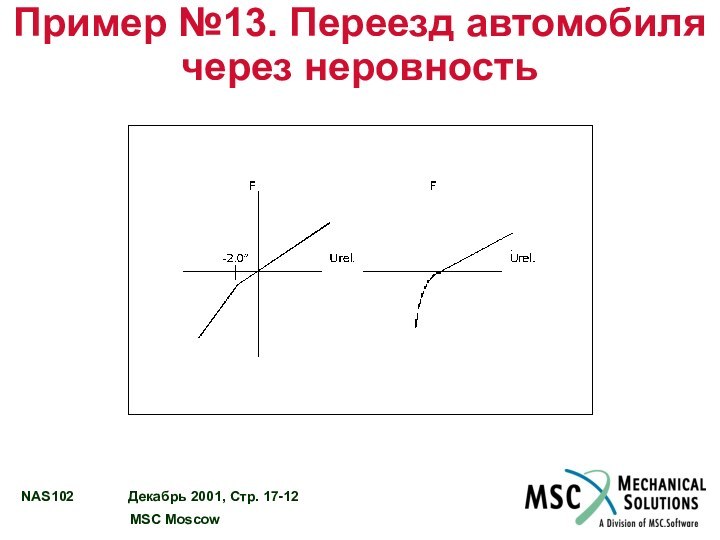
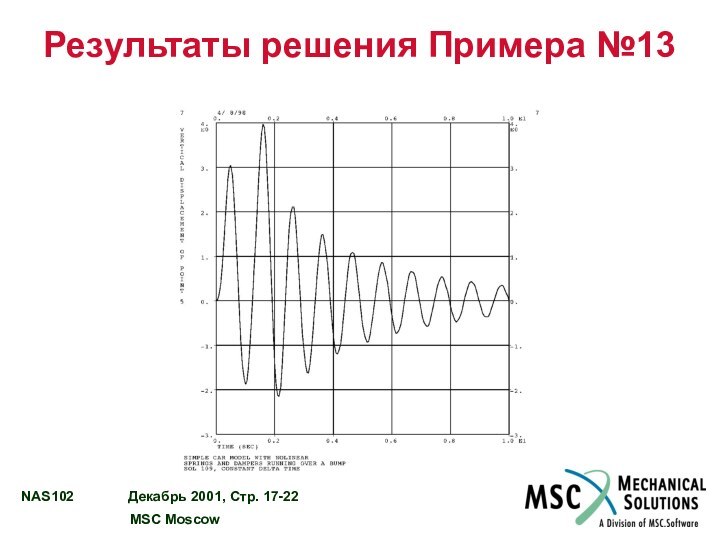
ПРИМЕР №13 – ПЕРЕЕЗД АВТОМОБИЛЯ ЧЕРЕЗ НЕРОВНОСТЬ………… 17 - 11
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №13..………………………….……………… 17 - 13
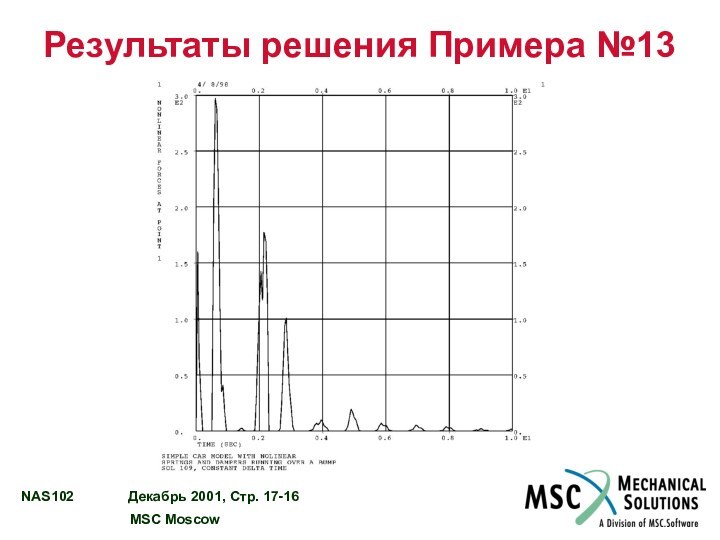
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №13.………………………………...……. 17 - 15

для представления не связанных с конструкцией переменных.
Задаются оператором EPOINT

в Bulk Data Section.
Могут использоваться только в остаточной структуре для динамического анализа (E-set - часть набора D-set).
Неподвержены никаким процедурам редуцирования, включая модальное редуцирование.
Не могут использоваться как конструкционные СС.
Не могут быть “связаны” (закреплены) посредством MPC или SPC.
Могут использоваться только в матрицах прямого ввода типа P и в передаточных функциях.
Могут подвергаться динамическому нагружению только посредством оператора DAREA в Bulk Data Section.

связей в форме:


где ud - зависимая переменная
u - независимая переменная
p - оператор дифференцирования

(p = d/dt)
Эквивалентны матрицам типа P, вводимым оператором DMIG (M2PP, B2PP, K2PP)
ПФ складываются с другими матрицами типа P. ud определяет строку матрицы, к элементам которой будут добавлены коэффициенты b0, b1, b2. ui определяет столбец, к элементам которого будут добавлены коэффициенты a0, a1, и a2.
Задаются оператором TF в Bulk Data Section, который инициируется оператором TFL в Case Control Section.

– нелинейная сила (момент), являющаяся функцией перемещения или скорости.

Задаются

операторами NOLINi в Bulk Data Section, инициируемыми оператором NONLINEAR Case Control Section.
Применяются только при анализе переходного процесса (должны прикладываться к переменным E-set при модальном методе решения или к переменным D-set при прямом методе решения).

зависимостей.







Наиболее просто используется при прямом методе решения: нелинейная сила

просто прикладывается к узлу. Модальный метод предполагает использование внешних переменных и передаточных функций, т.к. при модальной формулировке только к переменным E-set могут прикладываться нелинейные силы.

полученным на предыдущем шаге.


Меньшее значение Δt позволит получить большую

точность.
Нелинейные силы м.б. приложены только к переменным D-set (A-set + E-set) при прямом методе и H-set (modal set + E-set) при модальном методе. СС, к которым прикладываются нелинейные силы, не могут быть в наборе O-set, так же как и быть зависимыми.
При приложении сил по направлениям, не совпадающим с направлениями глобальной системы координат, необходимо использовать локальные системы координат. Отладьте эти приемы на “пилотной” модели.

перемещения


Функция скорости


NOLIN2 – нелинейная сила в форме “произведения” двух

таблиц

где Xj и Xk могут быть значениями двух перемещений или же двумя значениями одного и того же перемещения

функции положительного аргумента



где Xj может быть как перемещением, так

и скоростью
NOLIN4 - нелинейная сила в форме отрицательного значения экспоненциальной функции отрицательного аргумента



где Xj может быть как перемещением, так и скоростью

NOLIN

автомобиля через неровность, используя элементы NOLIN.

100 CEND TITLE= SIMPLE CAR MODEL WITH NOLINEAR SUBTITLE= SPRINGS AND

DAMPERS RUNNING OVER A BUMP LABEL= SOL 109, CONSTANT DELTA TIME SEALL= ALL SPC= 100 TFL= 100 NONLINEAR = 100 DLOAD = 100 TSTEP = 100 DISPLACEMENT(PLOT)= ALL NLLOAD(PLOT)= ALL $ OUTPUT(XYPLOT) CSCALE=1.3 XAXIS= YES YAXIS= YES XGRID LINES= YES YGRID LINES= YES XTITLE= TIME (SEC) YTITLE= VERTICAL DISPLACEMENT OF POINT 1 XYPLOT DISP/1(T2) YTITLE= VERTICAL DISPLACEMENT OF POINT 2 XYPLOT DISP/2(T2) YTITLE= VERTICAL DISPLACEMENT OF POINT 3 XYPLOT DISP/3(T2)

YTITLE= VERTICAL DISPLACEMENT OF POINT 4 XYPLOT DISP/4(T2) YTITLE= VERTICAL DISPLACEMENT OF POINT 5 XYPLOT DISP/5(T2) YTITLE= NONLINEAR FORCES AT POINT 1 XYPLOT NONLINEAR/1(T2) YTITLE= NONLINEAR FORCES AT POINT 2 XYPLOT NONLINEAR/2(T2) $ BEGIN BULK PARAM,POST,-1 $ $ CARRIAGE POINTS $ GRID, 1, , 0., 0., 0. GRID, 2, , 120., 0., 0. GRID, 5, , 60., 0., 0. $
$WHEEL POINTS $ GRID, 3, , 0., -10., 0. GRID, 4, , 120., -10., 0. $ $ CAR CARRIAGE $ CBAR, 5, 11, 1, 5, 0., 1., 0. CBAR, 6, 11, 5, 2, 0., 1., 0. PBAR, 11, 12, 10., 10., 10. MAT1, 12, 3.0E+7, , .33 $

RIGID-BODY MODES $ SPC1, 100, 1345, 1, 2, 5 SPC1, 100, 13456,

3, 4 $ $ SYSTEM WILL HAVE A NATURAL FREQUENCY OF 1 HZ $ WITH CRITICAL DAMPING OF 1 PERCENT $ CONM2, 10, 1, ,2.5 CONM2, 15, 2, ,2.5 CONM2, 20, 5, ,5. $ CELAS2, 30, 197.4, 1, 2, 3, 2 CELAS2, 40, 197.4, 2, 2, 4, 2 $ CDAMP2, 50, 1.88, 1, 2, 3, 2 CDAMP2, 60, 1.88, 2, 2, 4, 2 $ $ DEFINE EXTRA POINTS TO HOLD DIFFERENCES $ BETWEEN WHEELS AND CARRIAGE $ EPOINT, 101, 102 $ $ USE TRANSFER FUNCTIONS TO TRACK DIFFERENCES $ 101= V1 - V3 $ 102= V2 - V4 $ TF, 100, 101, 0, 1., 0., 0., , 1, 2, -1., 0., 0., , 3, 2, 1., 0., 0. $ TF, 100, 102, 0, 1., 0., 0., , 2, 2, -1., 0., 0., , 4, 2, 1., 0., 0. $ $ ADD NONLINEAR PORTION OF SPRINGS $

NOLIN1, 100, 1, 2, 197.4, 101, 0, 111 NOLIN1, 100, 2, 2, 197.4, 102, 0, 111 TABLED2, 111, -2.0, , -1., 1., 0., 0., 1., 0.,ENDT $ $ ADD NONLINEAR PORTION OF DAMPERS $ NOLIN4, 100, 1, 2, -0.3, 101, 10, 2. NOLIN4, 100, 2, 2, -0.3, 102, 10, 2. $ $ MOVE WHEELS OVER BUMP $ TLOAD2, 100, 222, 333, D, 0., 0.5, 1., -90. SPCD, 222, 3, 2, 4. SPCD, 222, 4, 2, 4. SPC1,100,2,3,4
DELAY, 333, 4, 2, 1.2 $ $ INTEGRATION INFORMATION TSTEP, 100, 200, .05, 1 $ ENDDATA

X Y - O U T P U T S U M M A R Y ( R E S P O N S E ) 0 SUBCASE CURVE FRAME XMIN-FRAME/ XMAX-FRAME/ YMIN-FRAME/ X FOR YMAX-FRAME/ X FOR ID TYPE NO. CURVE ID. ALL DATA ALL DATA ALL DATA YMIN ALL DATA YMAX 0 1 NONLIN 1 1( 4) 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 2.975151E+02 6.000001E-01 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 2.975151E+02 6.000001E-01 0 1 NONLIN 2 2( 4) 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.661460E+02 1.749999E+00 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.661460E+02 1.749999E+00 . . . . .
0 X Y - O U T P U T S U M M A R Y ( R E S P O N S E ) 0 SUBCASE CURVE FRAME XMIN-FRAME/ XMAX-FRAME/ YMIN-FRAME/ X FOR YMAX-FRAME/ X FOR ID TYPE NO. CURVE ID. ALL DATA ALL DATA ALL DATA YMIN ALL DATA YMAX 0 1 DISP 3 1( 4) 0.000000E+00 1.000002E+01 -2.836541E+00 2.199999E+00 5.942877E+00 4.500000E-01 0.000000E+00 1.000002E+01 -2.836541E+00 2.199999E+00 5.942877E+00 4.500000E-01 0 1 DISP 4 2( 4) 0.000000E+00 1.000002E+01 -2.671688E+00 1.999999E+00 7.464219E+00 1.600000E+00 0.000000E+00 1.000002E+01 -2.671688E+00 1.999999E+00 7.464219E+00 1.600000E+00 0 1 DISP 5 3( 4) 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.000000E+00 2.500000E-01 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.000000E+00 2.500000E-01 0 1 DISP 6 4( 4) 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.000000E+00 1.450000E+00 0.000000E+00 1.000002E+01 0.000000E+00 0.000000E+00 4.000000E+00 1.450000E+00 0 1 DISP 7 5( 4) 0.000000E+00 1.000002E+01 -2.150819E+00 2.149999E+00 3.963917E+00 1.600000E+00 0.000000E+00 1.000002E+01 -2.150819E+00 2.149999E+00 3.963917E+00 1.600000E+00