Слайд 2
Введение
Нечёткая логика — это раздел многозначной логики, который базируется
на обобщении классической логики и теории нечётких множеств, предложенной американским математиком
Лафти Заде в 1965 году для формализации нечётких знаний, характеризуемых лингвистической неопределённостью.
История
Применение
Преимущества
Недостатки
Вывод
Слайд 3
История
Основы нечеткой логики были заложены в конце 60-х
лет в работах математика Латфи Заде.
Для создания интеллектуальных
систем, способных адекватно взаимодействовать с человеком, был необходим новый математический аппарат, который переводит неоднозначные жизненные утверждения в язык четких и формальных математических формул.
Первым серьезным шагом в этом направлении стала теория нечетких множеств, разработанная Заде. Он же дал и название для новой области науки - "fuzzy logic" (fuzzy - нечеткий, размытый, мягкий).
Свое второе рождение теория нечеткой логики пережила в начале 80 годов, когда несколько групп исследователей всерьез занялись созданием электронных систем различного применения, использующих нечеткие управляющие алгоритмы.
Третий период начался с конца 80-х годов и до сих пор. До 90-ого года появилось около 40 патентов, относящихся к нечеткой логике.
Слайд 4
Применение
Во-первых, необходимо определить в общих словах области
применения нечеткого управления.
Использование нечеткого управления рекомендуется :
для очень сложных
процессов, когда не существует простой математической модели
для нелинейных процессов высоких порядков
если должна производиться обработка (лингвистически сформулированных) экспертных знаний
Использование нечеткого управления не рекомендуется, если:
приемлемый результат может быть получен с помощью общей теории управления
уже существует формализованная и адекватная математическая модель
Слайд 5
Применение
Вместо традиционных значений Истина и Ложь в нечеткой логике используется более широкий
диапазон значений, среди которых Истина, Ложь, Возможно, Иногда, Не помню (Как бы Да, Почему бы и
Нет, Ещё не решил, Не скажу…).
Наиболее важным применением теории нечетких множеств являются контроллеры нечеткой логики. Их функционирование несколько отличается от работы обычных
контроллеров; для описания системы
используются знания экспертов.
Слайд 6
Применение нечетких систем
Что касается отечественного рынка коммерческих систем
на основе нечеткой логики, то его формирование началось в
середине 1995 года. Популярными являются следующие пакеты:
CubiCalc 2.0 RTC - одна из мощных коммерческих экспертных систем на основе нечеткой логики, позволяющая создавать собственные прикладные экспертные системы ;
FuziCalc - электронная таблица с нечеткими полями, позволяющая делать быстрые оценки при неточных данных без накопления погрешности;
Слайд 7
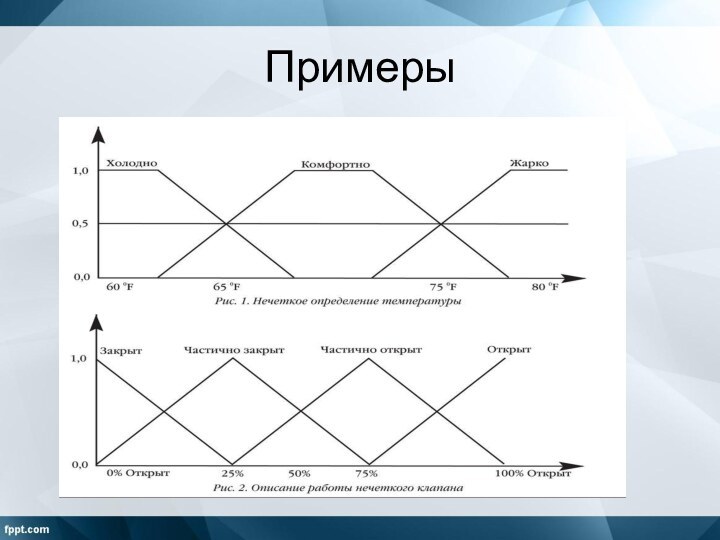
Примеры
Автоматическое управление воротами плотины на гидроэлектростанциях
Упрощенное управление роботами
Наведение телекамер при трансляции
спортивных событий
Эффективное и стабильное управление автомобильными двигателями
Управление экономичной скоростью автомобилей
Оптимизированное
планирование автобусных расписаний
Системы прогнозирования землетрясений
Медицина: диагностика рака
Распознавание рукописных текстов, объектов, голоса
Управление метрополитенами для повышения удобства вождения, точности остановки и экономии энергии
Оптимизация потребления бензина в автомобилях
Повышение безопасности ядерных реакторов
Слайд 9
Преимущества
Коротко перечислим преимущества fuzzy-систем по сравнению с другими:
возможность
оперировать нечеткими входными данными: например, непрерывно изменяющиеся во времени
значения , значения, которые невозможно задать однозначно
возможность нечеткой формализации критериев оценки и сравнения: оперирование критериями "большинство", "возможно", преимущественно" и т.д.;
возможность проведения быстрого моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности: оперируя принципами поведения системы, описанными fuzzy-методами, вы во-первых, не тратите много времени на выяснение точных значений переменных и составление описывающих уравнений, во-вторых, можете оценить разные варианты выходных значений.
Слайд 10
Недостатки
Недостатками нечетких систем являются:
отсутствие стандартной методики конструирования нечетких
систем;
невозможность математического анализа нечетких систем существующими методами;
применение нечеткого подхода
по сравнению с вероятностным не приводит к повышению точности вычислений.
Слайд 11
Вывод
Но все, же недостатки нечёткой логики не могут
перевесить ее достоинства, именно поэтому перспективы нечёткой логики, а
значит, нейросетевых подходов к решению прикладных и плохо формализуемых задач огромны и востребованы.